[ML/DL] 정보이론 기초

^{출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다.  Github Repo, Github Repo 2}

정보이론과 머신러닝

1. Entropy

1.1. 개념

어떠한 확률변수가 갖고 있는 정보의 양으로, 모든 사건의 확률 분포에서 얻을 수 있는 정보량의 기댓값을 의미한다. 1948년 Claude Shannon이 제안한 개념으로, 다음의 아이디어를 반영하고 있다.

• 확률이 큰 사건일수록 정보량은 작다.
• 독립적인 두 사건에서 얻을 수 있는 정보량은 두 사건에서 얻을 수 있는 정보량의 합이다.
• 정보량은 비트로 표현된다.

이 아이디어를 모두 반영하기 위해서 Shannon은 어떤 사건에서 얻을 수 있는 정보의 양을 해당 사건의 로그 확률로 정의했다. 그리고 어떠한 확률 분포에서 얻을 수 있는 정보량을 확률 이론의 기댓값 계산 방식에 따라 기댓값으로 나타냈다.

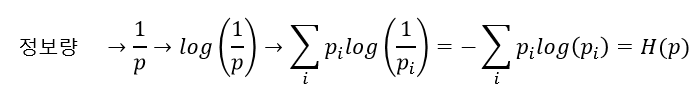
참고

교재에 명시되어 있는 정보 엔트로피 식은 정보량이 비트로 표현된다는 아이디어를 반영하지 않은 식이다. 이 부분은 강의에서 진행하지 않았으나, 추후 검색을 통해 찾아 반영해 작성한 내용이다. 원래 Shannon의 정보 엔트로피 식에서는 로그 확률의 밑이 2로 표현된다.

강사님께서는 정보 엔트로피와 열역학 엔트로피 사이의 연관 관계 및 그로부터 얻을 수 있는 정보 가치에 더 중점을 두어 설명하신 듯하다.

1.2. 엔트로피 공식 도출

섀넌이 정의한 엔트로피 공식은 \(H(x) = - \Sigma_{i=1}^n p_ilog(p_i)\) 이다.

그리고 이 식을 아래와 같이 변형해 보자.

\[\\ H(x) = \Sigma_{i=1}^n p_i*(-log(p_i)) \\ H(x) = \Sigma_{i=1}^n p_i*log(p_i^{-1}) \\ H(x) = \Sigma_{i=1}^n p_i*log(\frac {1} {p_i}) \\ H(x) = \Sigma_{i=1}^n log(\frac {1} {p_i})*p_i\]

한편, 확률 변수의 기댓값을 나타내는 공식은 \(E(X) = \Sigma_{i=1}^n x_i * p_i\) 이다.

\(x_i\) 자리에 \(log\) 값이 들어간 것 빼고는 변형된 엔트로피 공식의 맨 마지막 식과 전부 동일하다. 결국 엔트로피는 기댓값과 같은 형태를 갖고 있다.

여기서 \(log\) 부분은 정보의 양을 나타낸다. 섀넌의 아이디어에 따라 다음의 두 가지 조건을 만족하면 정보의 양을 나타내는 함수로 사용할 수 있다.

\[I(x) : 정보량을 \ 나타내는 \ 함수 \\ 1. \ p(x_1) > p(x_2) \rightarrow I(x_1) < I(x_2) \\ 2. \ I(x_1, x_2) = I(x_1) + I(x_2)\]

두 조건을 만족하는 모든 함수로 log만큼 좋은 게 없다(!).

참고

강사님의 교재에 설명되지 않은 부분이지만, 원래 섀넌 엔트로피 공식에서는 \(log\) 의 밑이 2이기 때문에, 정보의 양에 따라 필요한 bit 수를 구할 수 있게 된다.

1.3. 머신러닝에서의 의미

정보 이론에서의 엔트로피는 정보의 불확실성에 대한 척도를 의미한다. 따라서 불확실성을 수치로 표현하고, 그것을 줄이고자 하는 작업에 엔트로피 개념을 활용한다. 그리고, 머신러닝은 모델링을 통해 불확실한 정보를 줄이고, 혹은 불확실한 정보로부터 확실한 정보를 예측하고자 하는 작업이다. 따라서 머신러닝에서 엔트로피는 중요한 의미를 갖는다. (머신러닝과 정보 이론)

참고: 의사결정나무 알고리즘에서의 적용

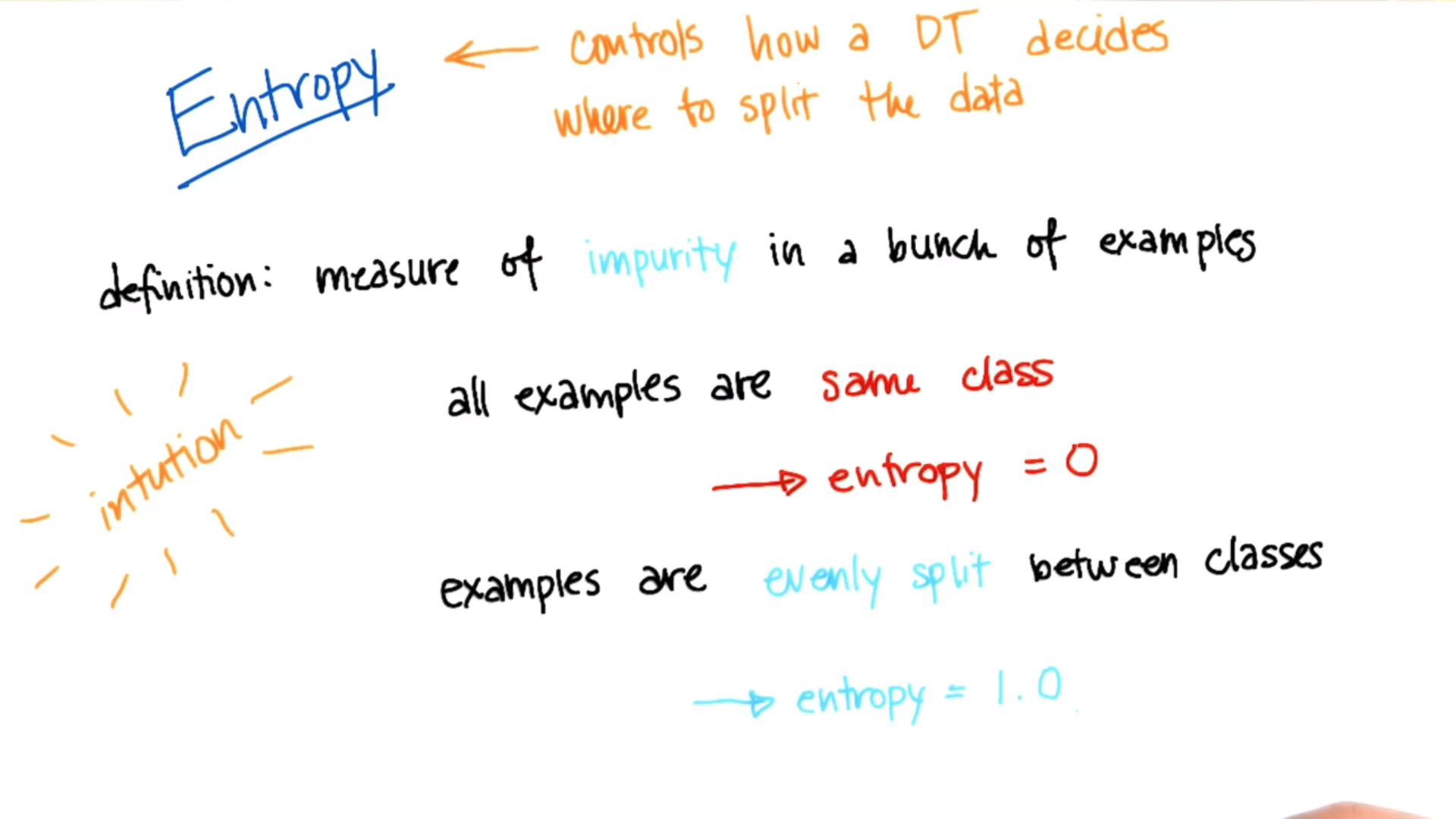
Decision Tree 수업 내용 및 아래 Udacity 강의 내용을 참고하자

Entropy	Impurity

^{https://www.youtube.com/watch?v=NHAatuG0T3Q} 

2. Cross Entropy

2.1. 개념

서로 다른 확률 분포 간의 정보 엔트로피이다. (서로 다른 두 확률 분포를 교차로 곱해 정보량을 계산한다는 의미에서 ‘크로스’란 이름이 붙는 듯하다.)

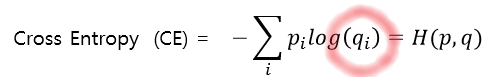
엔트로피 식에서 정보량을 정의하는 부분이 달라진다. 갑자기 p 자리에 q가 들어 왔다.

본래 엔트로피가 (특정 확률 분포에서 오는) 정보의 불확실성을 나타낸다고 하였다. 따라서 위의 식에 따르면, 크로스 엔트로피는 두 분포 P, Q의 차이 및 여기서 오는 정보의 불확실성이 된다.

2.2. 의미

기존의 엔트로피 식과 크로스 엔트로피 식을 조금 더 자세히 비교해 보자.

\[H(P) = \Sigma_{i=1}^n log(\frac {1} {p_i}) * pi \\ H(P, Q) = \Sigma_{i=1}^n log(\frac {1} {q_i}) * pi \\\]

엔트로피 식에서 log가 붙지 않은 부분이 실제 확률을 나타내고, log가 붙은 부분이 확률 분포가 나타내는 정보의 양을 나타낸다. 따라서 실제 확률 분포가 P일 때, 그 확률 분포로부터 얻을 수 있는 정보의 양을 나타낸 것이 엔트로피라면, 실제 확률 분포가 P일 때, 그와는 다른 어떠한 확률 분포 Q로부터 얻을 수 있는 정보의 양을 나타낸 것이 크로스 엔트로피가 된다.

이러한 정의 때문에, 크로스 엔트로피는 주로 틀릴 수 있는 분포에서 얻을 수 있는 정보의 양을 계산하는 데에 사용된다. 더 엄밀히 말하면, 실제 분포 P를 예측한 틀릴 수 있는 확률 분포 Q가 가지고 있는 정보량 혹은 불확실성을 나타낸다.

2.3. 계산 예시 및 특징

iris dataset을 분류하는 문제를 생각해 보자.

분류해야 하는 꽃의 품종이 Versicolor라고 하자. 그렇다면 실제 관측값에서 꽃이 Versicolor일 확률은 1, Setosa일 확률은 0, Verginica일 확률은 0이 된다. 편의상 각 클래스를 0, 1, 2로 하여 실제 관측값의 확률을 나타내면 다음과 같다.

\[y^t = [1 \ 0 \ 0]\]

머신러닝을 통해 모델링을 진행한 결과, 품종을 예측하기 위해 Q라는 확률 분포를 만들어 냈다고 하자. 이 때, 기계가 해당 확률 분포를 바탕으로 품종을 완전히 다르게 예측한 경우, 비슷하게 예측한 경우, 완전히 맞게 예측한 경우 Cross Entropy를 계산해 보자.

• 완전히 틀린 경우

\[y^t = [1.0 \ 0.0 \ 0.0] \\ y^p = [0.0 \ 1.0 \ 0.0] \\ CE = log\frac {1} {0.0} \times 1 + log\frac {1} {1.0} \times 0 + log\frac {1} {0.0} \times 0 = \inf\]

• 어느 정도 맞은 경우

  기계가 데이터를 보고, 해당 데이터가 Virginica일 확률을 0.7, Setosa일 확률을 0.1, Versicolor일 확률을 0.2라고 예측했다고 하자.

\[y^t = [1.0 \ 0.0 \ 0.0] \\ y^p = [0.7 \ 0.1 \ 0.2] \\ CE = log\frac {1} {0.7} \times 1 + log\frac {1} {0.1} \times 0 + log\frac {1} {0.2} \times 0 = 0.35667494393\]

• 완전히 맞은 경우

\[y^t = [1.0 \ 0.0 \ 0.0] \\ y^p = [1.0 \ 0.0 \ 0.0] \\ CE = log\frac {1} {1.0} \times 1 + log\frac {1} {0.0} \times 0 + log\frac {1} {0.0} \times 0 = 0\]

위의 계산 예시를 통해 크로스 엔트로피의 성질을 알 수 있다.

첫째, 크로스 엔트로피 값은 항상 엔트로피보다 크거나 같다. 직관적으로 이해하면, 크로스 엔트로피 값은 예측된 값을 바탕으로 실제 정보량을 계산하기 때문에, 완전히 맞게 예측하지 않는 한 틀린 정보를 가지고 있을 수밖에 없다. 따라서 실제 맞는 정보의 양보다 더 많은 정보를 가질 수밖에 없다.

둘째, 예측된 분포가 실제 분포와 비슷해질수록 크로스 엔트로피 값은 엔트로피 값과 가까워진다.

2.4. 머신러닝에서의 의미

서로 다른 두 확률 분포 간의 정보량 차이를 계산하는 것이 크로스 엔트로피이다. 이 때, 서로 다른 확률 분포로 원래의 확률 분포와 틀릴 수 있는 확률 분포 간 정보량 차이를 계산한다고 하자. 머신 러닝을 통해 예측 모형을 만드는 것은 훈련 데이터를 바탕으로 새로운 데이터를 예측할 수 있는 확률 분포를 만드는 것이다. 따라서 예측값과 실제값 간의 정보량 차이를 계산하고자 하는 목적에서, 크로스 엔트로피를 손실 함수로 사용한다.

훈련 데이터에 대해서는 실제 분포 P를 알 수 있기 때문에, 예측 모델에서의 확률 분포 Q와 실제 분포 P 간의 크로스 엔트로피 값을 계산할 수 있다. 이렇게 계산된 크로스 엔트로피 값은 실제 값과 모델이 예측한 값 사이의 정보 불확실성을 나타낸다. 따라서 손실함수로서 크로스 엔트로피를 사용하여 불확실성을 줄여 나가는 방향으로 학습이 이루어지게 되는 것이다.

특히 크로스 엔트로피의 성질을 상기시켜 본다면, 머신러닝의 학습이 잘 진행될수록 크로스 엔트로피 값과 엔트로피 값이 비슷해지게 되리라는 것을 알 수 있다. 따라서 크로스 엔트로피 값을 계산해서 학습 과정을 조정하면 머신러닝이 예측하는 확률 분포를 실제 확률 분포에 가깝게 만들 수 있는 것이다.

기존에 배웠던 손실함수인 MSE와 비교해서 살펴 보면, 모델의 정확도가 상승할수록 CE와 MSE가 모두 감소하는 것을 알 수 있다.

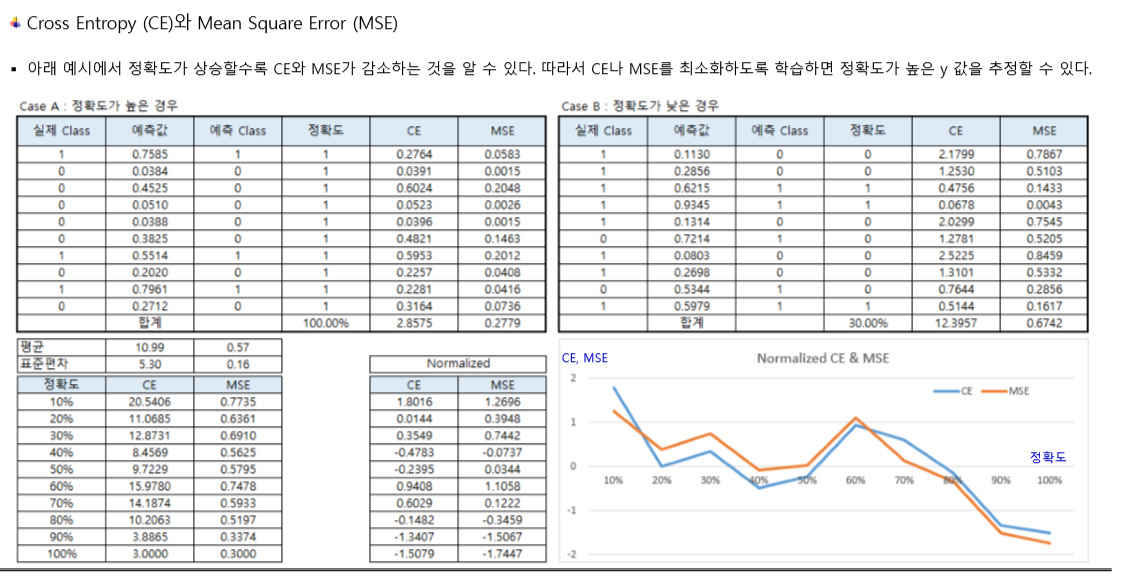
그리고 일반적으로 분류 문제에서는 MSE보다 CE를 사용하는 것이 더 좋다고 알려져 있다(이 부분에 대해서는 여기를 참고하자).

3. KL Divergence

3.1. 개념

두 확률 분포 간의 정보량 차이를 나타내는 개념이다. 각각의 확률 분포의 차이를 정보량 측면에서 수치화하는 것이다.

두 확률 분포의 차이를 ‘수치화’한다. 확률 분포의 차이를 수치화한다면, 실제 확률 분포에 가까운 분포와 그렇지 않은 분포의 차이를 알아낼 수 있다. 따라서 어떤 것이 더 예측을 잘 하는 확률 분포 인지 알 수 있다.

3.2. 의미

KL Divergence를 계산하는 식은 다음과 같다.

\[D_{KL}(P||Q) = - \Sigma \ P(x) log(\frac {Q(x)} {P(x)})\]

정보량 측면에서 KL Divergence 식을 파헤쳐 보자. 크로스 엔트로피 식을 전개하다 보면, KL Divergence 식을 도출할 수 있다!

\[H(p, q)(a.k.a \ Cross \ Entropy) \\ = -\Sigma p_i logq_i \\ = - \Sigma p_i logq_i \ -\Sigma p_i logp_i \ + \Sigma p_i logp_i \\ = H(p) + \Sigma p_i logp_i - \Sigma p_i logq_i \\ = H(p) + \Sigma p_i log \frac {p_i} {q_i}\]

결국 크로스 엔트로피 \(H(p, q)\) 는 원래 P의 엔트로피 \(H(p)\) 의 값에 마지막 항의 값 만큼을 더해준 것임을 알 수 있다. 이 때, 더해진 ‘무언가’ 가 바로 정보량 차이이고, 이 정보량 차이의 식이 자세히 살펴 보면 KL Divergence와 같음을 알 수 있다.

즉 , KL Divergence는 불확실한 분포를 통해 확실한 분포를 추정해 내고자 할 때, 두 분포의 크로스 엔트로피 값에서 실제 엔트로피 값을 만들기 위해 더해 주어야 하는 정보량 차이를 나타낸다. 이러한 의미에서 KL Divergence를 상대 엔트로피라고도 한다.

3.3. 특징

KL Divergence는 다음과 같은 특징을 갖는다. 수학적인 증명 과정은 강의 자료를 참고하고, 여기서는 다음과 같은 특징을 갖는다는 것만 알아두자.

• 0 이상이다.
• KL Divergence가 0이라는 것은, 두 확률 분포가 동치임을 나타낸다.
• 기준으로 두는 확률 분포에 따라 비대칭적인 값을 갖는다.

KL Divergence 값을 이해할 때 가장 중요한 것은, 두 확률 분포가 비슷할 수록 더 작은 값을 갖는다는 것이다. 결국 확률 분포의 차이를 수치화하고 싶다는 아이디어에서 출발한 개념이므로, 수치화되어 나타난 값이 작을수록 더 비슷한 확률 분포임을 보여 준다.

한편 마지막 특징은 KL Divergence를 검색하다 보면 항상 따라 나오는 ‘거리 개념이 아니므로 주의한다’는 말과도 연관된다. 만약 KL Divergence가 두 확률 분포 사이의 거리를 나타냈다면 P와 Q의 위치가 바뀌어도 같은 값을 가져야 하지만, 전혀 그렇지 않다. 참고로, 이러한 관점에서 KL Divergence를 대칭적으로 바꾼 Jenson-Shannon Divergence 식이 있다. 그 존재만 알아 두자

3.4. 머신러닝에서의 의미

머신러닝 모델링의 목적이 예측 확률 분포 Q를 실제 확률 분포 P와 가깝게 만들어 가는 것임을 상기해 본다면, 손실 함수로서 KL Divergence를 사용하는 것이 더 적절해 보인다. 두 함수의 정보량 차이를 줄여 나가야 하기 때문이다. 그렇다면 왜 머신러닝에서는 KL Divergence가 아니라 Cross Entropy를 손실함수로 이용하는 것일까?

결론적으로, KL Divergence와 Cross Entropy, 무엇을 최소화하든 그 결과는 같다.

위에서 KL Divergence와 Cross Entropy가 밀접한 관련이 있음을 식을 통해 알 수 있었다. 그런데, 머신러닝 학습 과정에서 예측 분포 Q의 파라미터를 조정해나갈 때 원래 확률 분포 P의 엔트로피는 변경되지 않는다. 원래 정해진 상수 값이다. 학습 과정에서 파라미터의 최적화를 통해 변경되는 것은 오로지 H(p, q), 즉, 크로스 엔트로피 값일 뿐이므로, KL Divergence값을 최소화하나, Cross Entropy를 최소화하나 거기서 거기다!

4. Mutual Information

정보량 관점에서 서로 다른 두 확률 변수가 서로 얼마나 연관되어 있는지를 나타낸다. 두 확률분포의 결합 확률분포와, 두 확률분포의 곱 간의 KL Divergence로 계산된다.

\[MI(X, Y) = KL(P(x, y)||p(x)p(y)) = \Sigma p(x, y)log_2(\frac {p(x, y)} {p(x)p(y)})\]

두 확률분포가 독립이라면 결합 확률분포가 두 확률분포 간의 곱과 같아진다. 따라서 독립일 경우, KL Divergence가 0이 되고, 그렇지 않다면 0보다 큰 어떤 값을 가지게 된다. 그리고 후자의 경우, 즉, 두 확률분포가 독립이 아닌 경우, 두 확률분포가 서로 연관되어 갖는 상호정보량을 위와 같은 식으로 측정하는 것이다.