Portfolio Selection

투자의 세계에 “계란을 한 바구니에 담지 말라”는 유명한 격언이 있다. 자산을 분산하여 투자하는 것의 중요성을 강조하는 말이다. 사실, 분산투자는 마르코비츠(Harry Markowitz)가 투자에 있어서 리스크에 대한 새로운 인식을 제시하기 전까지는 그다지 강조되지 않았었던 개념이다.

이 개념을 알기 위해, 마르코비츠가 1952년 Portfolio Selection 이란 논문에서 어떻게 포트폴리오 선택 및 분산 투자의 중요성을 강조하였는지, 그리고 이로부터 어떻게 현대 포트폴리오 이론이 전개되어 왔는지를 이해해야 한다.

1. Expected Returns Rule

포트폴리오 (선택) 이론이 등장하기 전까지, 투자에 있어서 통용되는 원리는 포트폴리오의 기대 수익률을 최대화하는 것이었다. 이를 Expected Returns Rule(이하 E rule)이라 한다. 이러한 E rule 하에서는 가장 큰 수익률을 갖는 증권(security)에 모든 자산을 투자하는 것이 행동 원리가 된다.

그 원리는 간단하다. $N$개의 증권이 있고, $R_i$를 각 증권으로부터 얻을 수 있는 할인된 현금 흐름의 가치라고 하자. 투자자는 가지고 있는(혹은 투자에 활용할 수 있는) 증권을 $N$개의 증권 각각에 대해 $X_i$의 비중으로 구성한다. 이 때 $X_i$는 다음의 두 가지 조건을 만족한다.

• $X_i \geq 0$ : 공매도 제외
• $\Sigma_{i=1} ^{N} X_i = 1$

이 $N$개의 증권들을 가지고 구성한 포트폴리오의 수익률을 $R$이라고 할 때, 포트폴리오의 수익률은 다음과 같다.

\[R = \Sigma_{i=1}^{N}X_iR_i\]

각 증권의 수익률 $R_i$가 확률 변수이므로, 그것들의 가중합인 $R$ 역시 확률 변수이다. 따라서 포트폴리오의 수익률을 최대화하고 싶다면, 그 기댓값 $E(R)$을 최대화하면 된다. 이것이 바로 E rule이다. 그리고 이러한 원칙에 따라 $E(R)$을 최대화하기 위해서, 투자자는 자신의 자산을 최대의 수익률을 갖는 자산에 모두 투자해야 한다. 만약, 최대의 수익률을 갖는 자산이 여러 개라면, 그 자산들만을 대상으로 분배 가중치 $X_i$의 합이 1이 되게만 투자하면 된다.

이러한 원칙 하에서는 다각화된 포트폴리오, 즉, 여러 개의 증권에 투자하는 포트폴리오가 다각화된 포트폴리오보다 그 어떤 경우에서도(in no case) 좋을 수 없다. 마르코비츠는 이러한 행위를 ‘투자(investment)’가 아닌 ‘투기(speculative behavior)’라고 본다.

2. E-V rule

이제 포트폴리오를 다각화하는 방식을 생각해 보자. 마르코비츠에 의하면 다각화는 실제 관찰(observed)되며, 이성적(sensible)인 행위이다.

참고 : 다각화 원칙의 도입

포트폴리오 다각화 원칙을 도입하면서 마르코비츠는 “There is a rule which implies that the investor should diversify and that he should maximize expected return.” 이라고만 서술한다. 그 당위성을 수학적으로 증명한 것은 아니다. 이전까지 통용되던 원칙에 의하면 포트폴리오를 다각화하는 것은 E rule의 지배 원리에 어긋났으므로, 그와 다른 새로운 원칙을 도입해 포트폴리오 다각화 인식의 기반을 마련했다는 것이 이 논문의 의의일 것이다.

과연 이러한 경우에도 1의 E rule이 적용될 수 있을까. 사실 통계학적으로 대수의 법칙(Law of Large Numbers)에 따르면 포트폴리오의 실제 수익률은 그 기댓값과 동일해진다. 그러나 포트폴리오의 기대 수익률을 구하는 과정에서는 LLN을 적용할 수 없다. 여러 증권들로 포트폴리오를 구성하면(=다각화), 각각의 증권들이 서로 관련되어 있어, 포트폴리오 수익률의 기댓값이 분산을 갖게 되기 때문이다. 따라서 포트폴리오의 기대 수익률을 구할 때는 그것을 구성하는 각 증권 간 상관관계 및 그로 인해 생겨나는 포트폴리오 수익률의 분산을 고려해야 한다.

개념

포트폴리오의 수익률의 분산이 클수록, 포트폴리오 수익률의 기댓값을 알기 어려워진다. 그러므로 포트폴리오 수익률의 변동성은 곧 해당 포트폴리오의 위험이다. 따라서 투자자는 다음과 같은 행동 원리를 보인다.

• 포트폴리오 수익률의 기댓값을 최대화하고 싶어 한다.
• 포트폴리오 수익률의 분산을 최소화하고 싶어 한다.

이렇게 (할인된) 포트폴리오 수익률의 기댓값을 desirable한 것으로, 그 분산을 undesirable한 것으로 보는 원칙을 Expected Returns - Variance of Returns Rule(이하 E-V rule)이라 한다. E-V rule 하에서는 포트폴리오 수익률의 기댓값이 최대가 된다고 해서 그 분산이 최소가 되지 않는다.

따라서 투자자는 포트폴리오를 구성할 때 두 가지를 고려해야 한다. 포트폴리오 수익률의 기댓값과 그 분산이다. 투자자가 포트폴리오 수익률의 분산을 감수하면서 그 기댓값을 늘리거나, 기댓값을 줄이면서 분산을 줄여야만 한다. 기댓값을 늘리면서 분산을 줄일 수는 없는 상충 관계가 있다는 것이다.

그 상충 관계를 살펴 보기에 앞서, E-V rule을 설명할 때 필요한 개념들을 정의하자. 포트폴리오 수익률 $R$이 그것을 구성하는 각각의 증권들의 가중합으로 주어진다는 것은 동일하다. 그리고 그 가중치 $X_i$가 만족해야 하는 조건 역시 1에서와 동일하다.

이제 $N$개의 증권들 중 $i$번째 증권의 수익률 $R_i$의 기댓값 $E(R_i)$를 $\mu_i$, $i$번째 증권과 $j$번째 증권의 수익률 간 공분산 $Cov(R_i, R_j)$을 $\sigma_{ij}$라 하자. 그러면 각 증권의 수익률의 분산 $Var(R_i)$는 $\sigma_{ii}$가 된다. 각 증권 간 수익률의 공분산은 각 증권 수익률 간 상관계수와 각 증권의 수익률의 표준편차를 이용해 $\sigma_{ij} = \rho_{ij}\sigma_{i}\sigma_{j}$로도 나타낼 수 있다. 이 때, 포트폴리오 수익률의 기댓값과 분산을 나타내면 다음과 같다.

\[E(R) = \Sigma_{i=1}^N X_i\mu_i\] \[Var(R) = \Sigma_{i=1}^N \Sigma_{j=1}^N X_i X_j \sigma_{ij}\]

상충 관계

마르코비츠는 3개의 증권이 존재할 경우로부터 기하학적으로 포트폴리오 수익률의 기댓값($E$)와 분산($V$) 간 상충 관계가 존재함을 보인다. 3개의 경우를 수학적/논리적으로 확장해 나가면 되기 때문에, $N$개 증권이 있을 때도 그 관계가 성립한다.

이 관계가 practical함이 증명되기 위해서는 다음의 두 가지 조건이 만족되어야 한다.

• 투자자는 E-V 원칙에 따라 행동한다.
• 합리적인 원칙에 따라 $\mu_i$와 $\sigma_{ij}$를 구할 수 있어야 한다.

참고 : $\mu_i$와 $\sigma_{ij}$

위의 두 가지 조건 중 두 번째 조건에 있어, 마르코비츠는 $\mu_i$와 $\sigma_{ij}$를 구할 수 있는 합리적인 방식이 있을 것이라 가정하고 넘어 간다.

We assume that the investor does (and should) act as if he had probability beliefes concerning these variables. (…) This paper does not consider the difficult question of how inverstors do (or should) form their probability beliefs.

사실 이것을 구해내는 게 이후 포트폴리오 이론 전개 및 자산 분배에 있어 중요하다고 할 수 있으나, 마르코비츠의 논문에서는 아이디어만을 제시했다.

3개의 증권이 있는 경우를 고려해 보자. 이 때 포트폴리오 수익률의 기댓값과 분산, 각 가중치는 다음의 조건을 만족한다.

\[E(R) = \Sigma_{i=1}^3 X_i\mu_i\] \[Var(R) = \Sigma_{i=1}^3 \Sigma_{j=1}^N X_i X_j \sigma_{ij}\] \[\Sigma_{i=1} ^3 X_i = 1\] \[\ X_i \geq 0 \ for \ i=1,2,3\]

$(6)$에 의해, $X_3 = 1 - X_1 - X_2 \ \cdots (6^{‘})$ 가 된다. $(6^{‘})$과 $(7)$을 이용해 3개의 증권으로 구성된 포트폴리오가 가질 수 있는 영역(attainable sets)을 $X_1 - X_2$ 평면에 나타내면 다음의 삼각형 $abc$가 된다.

이제 포트폴리오 수익률의 기댓값($E$)을 해당 평면에 나타내 보자. $(6^{‘})$과 $(4)$를 이용해 $E$를 나타내면, $E = \mu_3 + X_1(\mu_1 - \mu_3) + X_2(\mu_2 - \mu_3) \ \cdots (4^{‘})$이 된다. 이를 $X_2$에 대해 나타내면, 다음과 같은 직선의 방정식 형태가 됨을 알 수 있다. ($\mu_2 \neq \mu_3$을 가정한다.)

\[X_2 = \frac {E - \mu_3} {\mu_2 - \mu_3} - \frac {\mu_1 - \mu_3} {\mu_2 - \mu_3}X_1\]

따라서 $E$가 변할 때 직선이 상하로 수평이동하므로, 다음과 같은 $isomean$ 직선들을 얻을 수 있다.

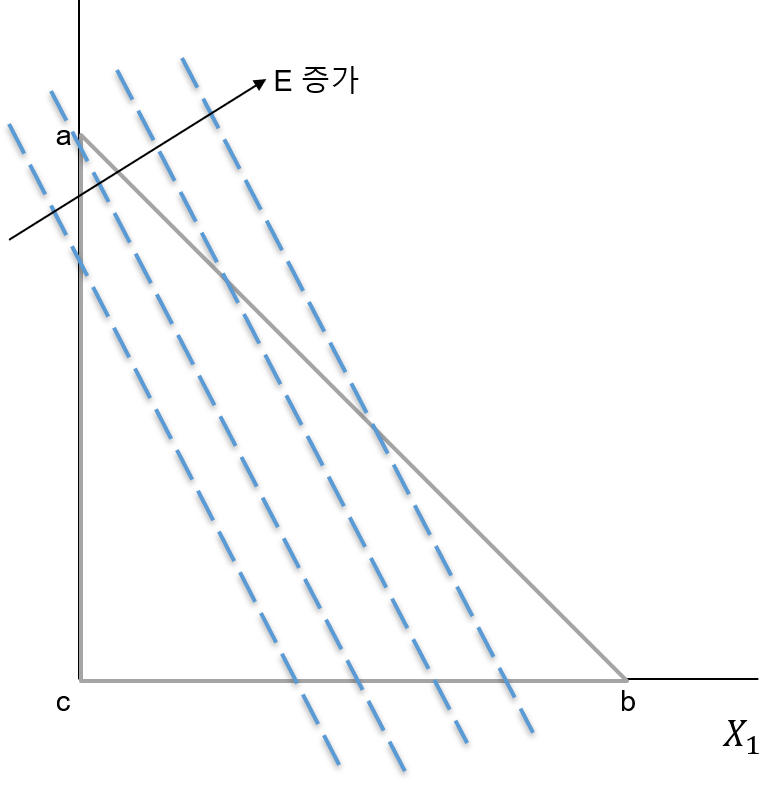
같은 방식으로 $(6^{‘})$과 $(5)$를 이용해 포트폴리오 수익률 분산의 식을 변형하면, $V = X_1^2(\sigma_{11} - 2\sigma_{13} + \sigma_{33}) + X_2^2(\sigma_{22} - 2\sigma_{23} + \sigma_{33}) + 2X_1X_2(\sigma_{12} - \sigma_{13} - \sigma_{33} + \sigma_{33}) + 2X_1(\sigma_{13} - \sigma_{33}) + 2X_2(\sigma_{13} - \sigma_{33}) + \sigma_{33} \ \cdots (5^{‘}) $이 된다. 이를 해당 평면에 나타내면, 다음과 같은 $isovariance$ 타원들을 얻을 수 있다. 이 때 타원의 중심 $\mathbf{x}$는 포트폴리오 수익률의 분산이 최소가 되는 점을 의미한다.

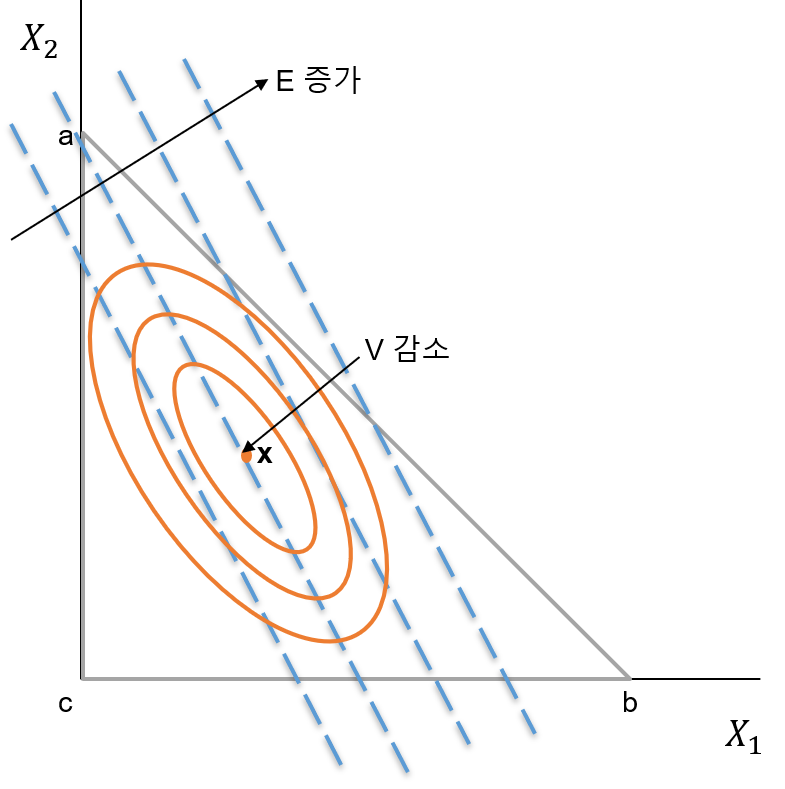
참고 : $isovariance$ 타원

사실 이 부분에 있어서는 논문에 명확한 수학적 식 변형이 제시되어 있지는 않다. 다만 수학적으로 2차 곡선의 판별식을 통해 $(5^{‘})$의 식이 어떤 형태를 띠는지 확인해 보면, 타원임을 알 수 있다. 타원의 중심의 좌표를 구하는 것은 매우 복잡한 일이며, 마르코비츠도 해당 타원의 중심의 좌표를 논문에 제시하지는 않았다. 대신 그 중심의 좌표가 attainable set을 나타내는 삼각형 $abc$ 안에 있거나 밖에 있는 경우 모두 상충 관계가 있다는 것을 기하학적으로 보여준다. 해당 포스트에서는 전자의 경우에 대해서만 다룬다.

이제 $E$와 $V$ 간의 관계를 파악할 수 있다. desirable한 $E$를 늘리는 방향으로 이동하고자 하면, undesirable한 $V$도 커진다. 반대로 undesirable한 $V$를 줄이고자 할 경우, desirable한 $E$도 작아진다.

효율적 투자 집합

위와 같은 상충 관계를 이용해 효율적 투자 집합(efficient sets)을 찾을 수 있다. 가능한 모든 $E$를 생각해 보자. 각각의 $E$를 나타내는 직선과 $V$가 접하는 지점이 바로 주어진 $E$에서 포트폴리오 수익률의 분산이 최저가 되는 점이다. $V$를 나타내는 타원이 attainable set 영역 밖에 있는 경우 이 점은 attainable set 위의 점으로 나타나게 된다.

이러한 점들을 모으면 curve 형태가 될 것이고, 이를 critical line $l$이라 한다. 그리고 이 선 $l$ 위에 존재하는 모든 포트폴리오가 일정 정도의 포트폴리오 수익률 기댓값 $E$를 추구하고자 할 때, 투자자가 포트폴리오 수익률의 분산 $V$를 최소로 만들 수 있는 효율적 지점들이다.

위의 모든 논의들을 종합하면 다음 그림과 같다.

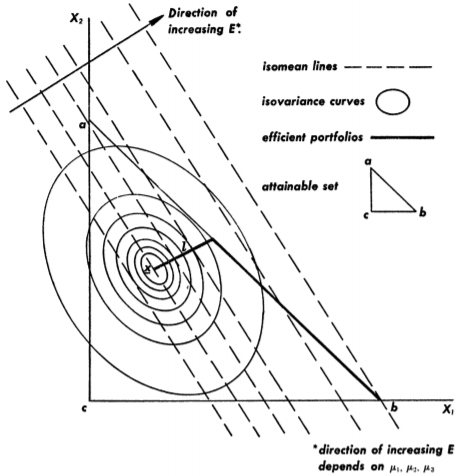
이제 모든 포트폴리오의 attainable set을 $E-V$ 평면에 나타내자. 그러면 E-V rule의 지배원리 하에서, 효율적인 투자 집합들은 주어진 $E$에서 $V$를 최소화하거나, 주어진 $V$에서 $E$를 최대화하는 포트폴리오의 집합이므로, 다음 그림에서와 같이 확정적으로 나타나게 된다.

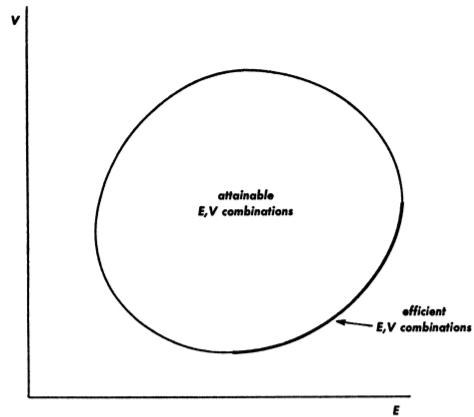
3. 결론

마르코비츠는 이러한 E-V rule이 투자를 투기가 아닌 관점에서 설명할 때 더 적합한 원칙이라고 말한다. 한편으로 E-V rule을 따르는 경우, 다각화를 위해 어떤 방식을 택해야 할지도 알 수 있다. 다각화를 위해서는 포트폴리오를 구성하는 증권의 수가 많을수록, 그리고 포트폴리오를 구성하는 증권 간 공분산(혹은 상관관계)가 낮을수록 좋다.

이후 마르코비츠는 E-V 원칙을 사용할 수 있는 분야에 대해 제언한다. 첫째는 이론적 분석(theoretical analyses)이다. 이 분야에서는, 예컨대, 투자자의 포트폴리오 수익률의 기댓값과 분산 사이에서의 선호가 변할 때 어떠한 변화가 있을 수 있는지, 증권시장에서 공급의 변화가 있을 때 포트폴리오 선택이 어떻게 변화할 것인지 등을 이론적으로 분석할 수 있을 것이다.

둘째는, 증권의 선택(selection of securities)이다. 이 부분은 마르코비츠가 명확하게 밝히지 않았던 부분이지만, 그가 주장하는 포트폴리오 선택의 과정에서 중요한 위치를 차지한다.

서두에 그는 포트폴리오 선택이 두 단계를 거친다고 이야기한다. 1단계는 증권 선택(Security Selection)으로, 증권 시장에 대한 관찰과 경험(observation and experience)을 바탕으로, 투자자가 선택할 수 있는 증권들의 미래 성과가 어떻게 될지 probability belief를 형성하는 과정이다. 2단계는 포트폴리오 선택(Choice of Portfolio)으로, relevant beliefs를 기반으로 실제 자산을 분배(allocating strategy)하는 과정이다.

포트폴리오 선택에서의 1단계가 첫째 분야와 연관된다면, 2단계는 둘째 분야와도 연관된다. E-V rule을 적용하기 위해서는 합리적인 방법을 통해 $\mu_i, \sigma_{ij}$를 찾아내야 한다. 이전의 논리 전개에 있어 마르코비츠가 적절한 통계 기법을 통해 찾을 수 있다고 가정하고 넘어갔던, 바로 그 부분이다. 마르코비츠가 제안하는 한 가지 방법은 historical data를 이용하는 것이지만, 더 나은 방법들이 있을 것이라 이야기한다.

결과적으로 그의 논문은 포트폴리오 다각화의 필요성 및 다각화를 위한 변동성 개념의 도입에서 큰 의의를 가진다. 한편으로 그의 이론 및 결론 부분의 제언을 시작으로 현대 포트폴리오 이론이 발달하게 된다. E-V rule을 기반으로 CAPM 이론 등이 나타나며, 증권 선택 단계에서 $\mu_i, \sigma_{ij}$를 찾아 내기 위한 연구들도 나타난다.

그러므로, 마르코비츠를 알지 않고서는 현대 금융 이론 및 포트폴리오 이론을 논할 수가 없다!