[DL] Competitive Learning_2.구현

7 분 소요

^{출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다.} ^{Github Repo}

^{Tensorflow : 2.2.0}

Competitive Learning: 코드로 구현하기

이전에 KMeans 실습을 진행했을 때와 비슷하게, 군집을 형성하는 임의의 NumPy 데이터를 생성하고, Competitive Learning 알고리즘을 적용해 군집화해 본다.

1. 모듈 불러오기 및 데이터 생성

# module import
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt

# create Data
def createData(n):
    xy = []
    for i in range(n):
        r = np.random.random()
        
        # r 기준으로 3부류의 데이터 생성
        if r < 0.33:
            x = np.random.normal(0.0, 0.9)
            y = np.random.normal(0.0, 0.9)
        elif r < 0.66:
            x = np.random.normal(1.0, 0.3)
            y = np.random.normal(2.0, 0.3)
        else:
            x = np.random.normal(3.0, 0.6)
            y = np.random.normal(1.0, 0.6)
        
        xy.append([x, y])
    
    return pd.DataFrame(xy, columns = ['x', 'y'])

더 생각해볼 점

지난 번 수업 때도 느꼈던 건데, r만 잘 설정하면 굳이 3개로 제한하지 않아도 여러 개의 군집 데이터를 형성할 수 있을 것 같다. 생성하고자 하는 군집 개수 인자로 받아서, np.linspace로 구간 나누고 r 구간 따라서 x, y 좌표 생성해 주면 될 것 같다.

그렇게 구현해보려고 했는데, 문제는, np.random.normal의 평균과 표준편차를 어떻게 잡아야 되는지 모르겠다. 혹시 Scikit-learn의 make_blobs 함수가 어떻게 군집을 이루는 점을 만들어내는지 그 원리를 이해하면 될 수 있지 않을까 했는데 ㅎ… 지금의 나한테는 좀… 어려운 듯(^^;;)하다.

2. Instar 알고리즘

먼저 Instar 알고리즘을 따라 경쟁학습을 구현해 보자. 하나의 winner 뉴런을 찾아, 그에 해당하는 가중치를 Hebb 규칙으로 업데이트한다.

2.1. 승자 뉴런 찾기

Winner 뉴런을 찾는다.

distance : 데이터와 가중치 뉴런 간 거리를 계산한다. 여기서는 유클리디안 거리 계산 방식을 사용했다.
winner : 거리가 가장 가까운 뉴런의 번호(index)를 tf.argmin 함수를 통해 찾는다. 이 뉴런이 승자가 된다.
dist : 나중에 거리 계산을 위해 함께 반환하는 것일 뿐, 큰 의미는 없다. KMeans 알고리즘에서 distance를 에러로 사용했던 것과 비슷하게 비교하기 위한 목적이다. tf.slice 함수를 이용해 winner 위치에 있는 거리를 가져 온다.

# winner neuron 찾기
def findWinner(W, X):
    distance = tf.sqrt(
    	tf.reduce_sum(
        	tf.square(tf.subract(W, tf.transpose(X))
            ), axis=1)
    	)
    winner = tf.argmin(distance, axis=0)
    dist = tf.slice(distance, [winner], [1])
    
    return dist, winner   

2.2. 가중치 업데이트

Hebb's Rule에 따라 가중치를 업데이트한다.

to_be_updated : tf.gather 함수를 이용해 승자 뉴런의 가중치를 가져 온다. 해당하는 뉴런의 가중치만 업데이트할 것이다.
weight_updated : Hebb's Rule에 따라 가중치를 업데이트하는 식이다.
new_weight : winner 자리에 해당하는 가중치만 업데이트한다. 가중치 텐서가 애초에 tf.Variable로 선언되었기 때문에, tf.tensor_scatter_nd_update 함수를 이용해서 업데이트해주어야 한다.

# Hebb's Rule에 따라 가중치 업데이트
def updateWeights(W, winner, X, alpha):
    '''
    W: 초기 가중치,
    winner: winner neuron 번호,
    X: 데이터
    '''
    to_be_updated = tf.gather(W, winner)
    weight_updated = tf.add(to_be_updated, tf.multiply(alpha, tf.subtract(tf.transpose(X), to_be_updated)))
    new_weight = tf.tensor_scatter_nd_update(W, [[winner]], weight_updated)
    
    return new_weight

2.3. 승자 뉴런 전달

승자 뉴런의 가중치만을 업데이트한다. 원래 복층 신경망을 구성하여 경쟁학습 모델을 구성할 때 유용하게 활용하는데, 이후 진행될 실습 코드에서는 단층 신경망을 구현하기 때문에, 큰 역할은 하지 않는다.

복층 신경망에서라면 승자 뉴런을 원핫 벡터로 변환하여 그 다음 층으로 전달하는 역할을 한다. 이 함수에서 반환되는 첫 번째 값 r이 원핫 인코딩된 뉴런 벡터고, 두 번째 값이 해당 뉴런이 클러스터링되는 라벨을 의미한다.

조금 더 자세히 살펴 보면, tf.one_hot을 통해 승자 뉴런의 출력값만 1로 설정하고, 나머지 뉴런의 출력값은 0으로 설정하는 것이다. 만약 복층 신경망이었다면, 이 출력값이 다음 layer로 전달되는 것이다.

def winnerTakesAll(W, W, n):
    _, winner = findWinner(W, X)
    r = tf.one_hot(winner, n)
    
    return r, tf.argmax(r, 0)

2.4. 경쟁학습 구현

단층 신경망을 구성한다.

# load data
n = int(input('데이터 좌표 수를 설정하세요.: '))
data = createData(n)

# data 변환
input_data = data.values.T.astype(np.float32)

# 파라미터 설정
n_input = int(input('입력 뉴런 노드 수를 설정하세요.: '))
n_output = int(input('출력 뉴런 노드 수를 설정하세요.: '))
ALPHA = float(input('헵 학습률을 설정하세요.: '))
epochs = int(input('학습 횟수를 설정하세요.: '))

# 그래프 생성
Wo = tf.Variable(tf.random.normal([n_output, n_input]), dtype=tf.float32)

# 학습
for epoch in range(epochs):
    error = 0 # 거리 개념
    
    for k in range(n): # X좌표 각각에 대해 아래의 작업 수행
        X_data = input_data[:, k].reshape([n_input, 1])     
        # 1) winner neuron 찾기
        dist, win = findWinner(Wo, X_data)        
        # 2) winner neuron 가중치 업데이트
        Wo = updateWeights(Wo, win, X_data, ALPHA)
        # 3) 에러 측정
        error += dist.numpy()[0]

    print("%d-th epoch done. Error: %.8f" % (epoch, error / n))

학습 과정을 살피기 전에, 제발 shape 에 주의하자. 처음에 출력 뉴런 가중치 행렬 shape 이상하게 줬다가 진땀 뺐다. 사실 내가 처음에 오류 냈을 때처럼 가중치 행렬 shape 설정해도 되지만, 그러려면 위에서 데이터를 전치하고 형 변환하는 부분도 다시 설정해주어야 한다. 어떻게 해도 상관 없으나, 중요한 것은 shape을 반드시 맞춰주어야 한다는 점이다.

잘못 설정한 Wo

처음에 Wo = tf.Variable(tf.random.normal([n_input, n_output]), dtype=tf.float32) 이라고 설정했고, InvalidArgumentError: Incompatible shapes: [2,3] vs. [1,2] [Op:Sub] 에러가 났다. 디버깅 위해 shape을 찍어 보니 실제로 그렇더라. weight: (2, 3), input data: (2, 1)

~~컴퓨터가 뭔 잘못이니. 내 잘못이지 다.~~

각 데이터의 형태를 보자. input_data는 (1000, 2) 형태이다. 다시 한 번 말하지만, 강사님이 편의를 위해 일부러 전치해서 가로(?)로 길게 늘여 놓은 형태이다. 기존에 데이터를 생성할 때는 (2, 1000) 형태로 생성되어 있었다.

학습을 과정을 보자. 각각의 학습 epoch 안에서, X좌표 각각에 대해 1), 2), 3)의 과정을 차례로 수행한다.

좌표를 n개 생성했기 때문에, 각각의 입력 데이터에 대해 인덱싱을 통해 k번째 좌표를 가져 온다. 그리고 이것을 신경망 입력 형태에 맞게 reshape한다.

군집학습의 개념이 원래 에러 측정의 개념이 없지만, 각 중점에 할당된 데이터까지 거리의 합으로 에러를 측정한다. 이후 총 에러를 n으로 나눠야 그 학습 에폭 안에서의 최종 오차를 측정할 수 있다.

2.5. 클러스터 결정

위의 과정을 거쳐 학습이 완료되었으면, winnerTakesAll 함수를 사용해 클러스터 라벨을 반환하자.

# 클러스터 라벨을 저장할 배열
cluster = []

# 클러스터 라벨 결정하여 저장
for k in range(n):
    data_X = input_data[:, k].reshape([n_input, 1])
    _, label = winnerTakesAll(Wo, data_X, n_output)
    cluster.append(label.numpy())

2.6. 결과 확인

학습이 완료된 Wo는 KMeans의 Centroid 역할을 한다. 결국 거리가 가장 짧은, 데이터의 형태를 가장 닮은 Weight 행렬이 형성되었을 것이기 때문에, 그 의미는 KMeans의 중점과 동일하다.

중점을 확인하고, 각 데이터의 군집화 결과를 시각화하자.

# 학습이 완료된 weight 확인
centroids = Wo.numpy()
print(centroids)

# plot 
clust = np.array(cluster)
data = input_data.T
color = plt.cm.rainbow(np.linspace(0, 1, n_output))
plt.figure(figsize=(8, 6))

for i, c in zip(range(n_output), color): # 전체 데이터 그림
    print(i, c)
    plt.scatter(data[clust==i, 0], data[clust==i, 1],
                s=20, color=c, marker='o',alpha=0.5,
                label=f"cluster-{i}")
    
plt.scatter(centroids[:, 0], centroids[:, 1], # 클러스터 그림
            s=250, marker='^', color='black', label='centroids')
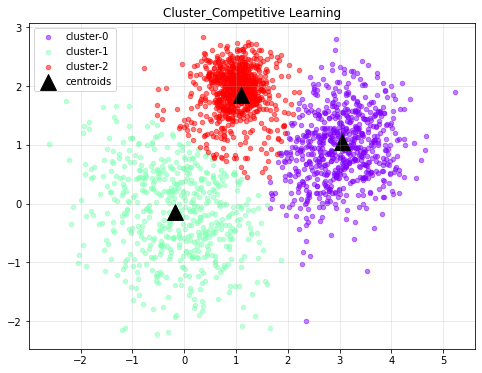
plt.title('Cluster_Competitive Learning')
plt.legend()
plt.grid(alpha=0.3) 
plt.show()

클러스터링 결과를 확인하면 다음과 같다.

3. SOM 알고리즘

이제 SOM 알고리즘을 이용해 경쟁학습을 구현해 보자. 단계별로 끊기 보다, 전체 흐름을 확인하는 데에 중점을 둔다.

Instar 알고리즘과 다른 부분은 winner 뉴런의 주변 이웃 뉴런들까지 가중치 업데이트의 대상으로 같이 선택한다는 점이다. 그리고 처음에는 해당하는 이웃의 범위를 넓게 설정했다가, 점차 줄여 나간다.

이것이 코드로 어떻게 구현되는지에 초점을 두어 다음의 코드를 이해하자.

MNIST 데이터로 실습을 진행한다.

# module import 
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import KernalPCA
import pickle

# load MNIST data
with open(f'{data_path}/mnist.pickle', 'rb') as f:
    mnist = pickle.load(f)
    
# 승자 뉴런 찾기
def findWinner(W, X):
    distance = tf.sqrt(tf.reduce_sum(tf.square(tf.subtract(W, tf.transpose(X)), axis=1)))
    winner = tf.argmin(distance, axis=0)
    dist = tf.slice(distance, [winner], [1])    
    return dist, winner

# 승자 뉴런 가중치 업데이트
def updateWeights(W, winner, X):
    to_be_updated = tf.gather(W, winner)
    weight_updated = tf.add(to_be_updated, tf.multiply(alpha, tf.subtract(tf.transpose(X), to_be_updated)))
    new_weight = tf.tensor_scatter_nd_update(W, [[winner]], weight_updated)
    return new_weight

# 승자 독식
def winnerTakesAll(W, X, n):
    _, winner = findWinner(W, X)
    r = tf.one_hot(winner, n)
    return r, tf.argmax(r, 0)

# 입력 데이터 생성
X_train = mnist_data[:3000, :]
image_X = input_X.copy() # 이후 이미지 그릴 때 확인용
y_train = mnist.target(:3000) # 원래 라벨 필요 없지만, 나중 확인용.

# 표준화
scaler = StandardScaler()
X_train = sc.fit_transform(X_train.T).T

# 차원 축소
pca = KernelPCA(n_components=100, kernel='rbf')
X_train = pca.fit_transform(X_train)

# 데이터 형 변환
X_train = X_train.astype(np.float32).T

# 파라미터 설정
n_input = X_train.shape[0]
n_output = np.unique(X_train).shape[0]
ALPHA = 0.05
loadWeights = False

# 그래프 생성
if loadWeights:
    with open(f'{data_path}/comp_weights1.pickle', 'rb') as f:   
        Wh = pickle.load(f)
        n_neighbor = 0
else:
    Wo = tf.Variable(tf.random.uniform([n_output, n_input]))
    n_neighbor = n_output - 1

    
# 이미지 한 개씩 입력하며 반복 학습
n = X_train.shape[1]
for i in range(50):
    error = 0
    for k in range(n):
        x = X_train[:, k].reshape([n_input, 1])
        dist, win = findWinner(Wo, x)
        
        # 1) 이웃 범위 설정
        winner_min = np.max([0, win.numpy() - n_neighbor])
        winner_max = np.min([n_output - 1, win.numpy() + n+neighbor])
        
        # 2) 가중치 업데이트
        for m in range(winner_min, winner_max):
            Wo = updateWeights(Wo, m, x)
        
        # 에러 기록
        err += dist.numpy()[0]
        
    # 3) 이웃 범위 감소
    n_neighbor = np.max([0, n_neighbor -1])


(...)
# Wo, Wh를 저장해 둔다.
with open('dataset/comp_weights1.pickle', 'wb') as f:
    pickle.dump(Wo, f, pickle.HIGHEST_PROTOCOL)
(...)

이전에 머신러닝 때 KMeans와 DBSCAN으로 MNIST 데이터를 클러스터링한 적이 있다. 그 떄와 동일하게 전처리했다. 이미지 데이터의 경우 1) feature별로 scaling하는 것이 아니라, 하나의 평활화된 이미지 벡터에 대해 표준화해야 한다는 것과, 2) 커널 PCA로 차원을 줄인다는 것이다.

loadWeights의 경우 boolean 변수로, 학습 데이터가 커질 때 중간 중간 가중치를 저장하고 불러오는 역할을 담당한다. 지금은 일부러 데이터가 커서 3000개만 이용하므로, False로 설정한다.

이전과 동일한 방식으로 가중치 행렬을 tf.Variable로 생성한다. 역시나, shape에 주의하자.

위의 코드에서는 처음 neighbor의 수를 전체 출력 노드의 수보다 1 적게 설정하여 계속 줄여가도록 했다. 그러나 이는 전적으로 분석자의 판단에 따르는 것이다.

1)에서 3) 까지가 SOM 알고리즘의 핵심인 neighbor 개념을 구현한 예이다. winner_min, winner_max로 이웃의 범위(window 느낌?)를 설정하고, 해당 구간에 있는 모든 가중치에 대해 updateWeights 함수를 적용한다. 그리고 3)에서 이웃의 범위를 좁힌다.

참고

왜 -=1 사용하지 않고, 이웃의 범위 좁히는 데 max 함수 사용했을까?

그 이후 부분은 위와, 그리고 이전의 KMeans, DBSCAN 실습에서 했던 내용과 비슷하기 때문에 여기서는 생략한다.

Twitter Facebook LinkedIn

이레이저

[DL] Competitive Learning_2.구현

Competitive Learning: 코드로 구현하기

1. 모듈 불러오기 및 데이터 생성

2. Instar 알고리즘

2.1. 승자 뉴런 찾기

2.2. 가중치 업데이트

2.3. 승자 뉴런 전달

2.4. 경쟁학습 구현

2.5. 클러스터 결정

2.6. 결과 확인

3. SOM 알고리즘

공유하기

댓글남기기

참고

[AI] SlowFast Demo 실행

[AI] DL GPU 개발환경 구축 - WSL

[k8s] Kubernetes 환경에서 Argo Workflow Artifact 기능 사용하기

«TODO» [k8s] Kubernetes 환경에서 PyTorch 공유 메모리 설정하기