[DL] RNN

^{조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo}

^{Tensorflow : 2.2.0}

RNN 모델 이해하기

음악, 동영상, 주가, 글 등 순서를 갖는 데이터를 처리하는 대표적인 모델로 RNN 모델이 있다. RNN은 기존의 신경망 모델과 달리 이전 스텝의 출력값을 다시 다음 스텝의 입력값으로 사용함으로써, 시퀀스(시간적으로 순서를 갖는 데이터)의 구조를 분석할 수 있다.

지금 과정과의 연관성도 상당히 높은 모델이다. 그러나 RNN은 뒤에서도 살펴 볼 Vanishing Gradient 문제로 인해, 요즈음에는 RNN의 단점을 개선한 LSTM 모델을 주로 사용한다. 실제 RNN이라고 한다면 순환신경망 계열의 모델 모두를 통틀어 이야기하기도 한다.

따라서 이 단계에서는 RNN에서 각 입력 데이터 간 순환이 어떻게 이루어지는지, 그로 인한 문제가 무엇인지 파악하는 데에 초점을 두자.

1. Vanila RNN

기존에 살펴 본 여러 신경망 (Logistic Regression, Competitive Learning 무엇이든 그러하다) 의 구조들을 떠올려 보자. 입력 - 은닉 - 출력층으로 이어진 일방향적 신경망이다. 입력층을 거치고, 은닉층을 거치고, 출력층을 거친다. 이러한 네트워크 구조를 Feed Forward Network라고 한다.

^{강사님 말씀으로는 앞쪽으로 계속 먹이를 주는 네트워크라고..}

RNN은 Recurrent Neural Network를 의미한다. Recurrent라는 말의 의미에서 풍기는 뉘앙스가, 무언가 재현되고 다시 일어나는 것 같다.

RNN 셀의 구조를 나타내면 다음과 같다.

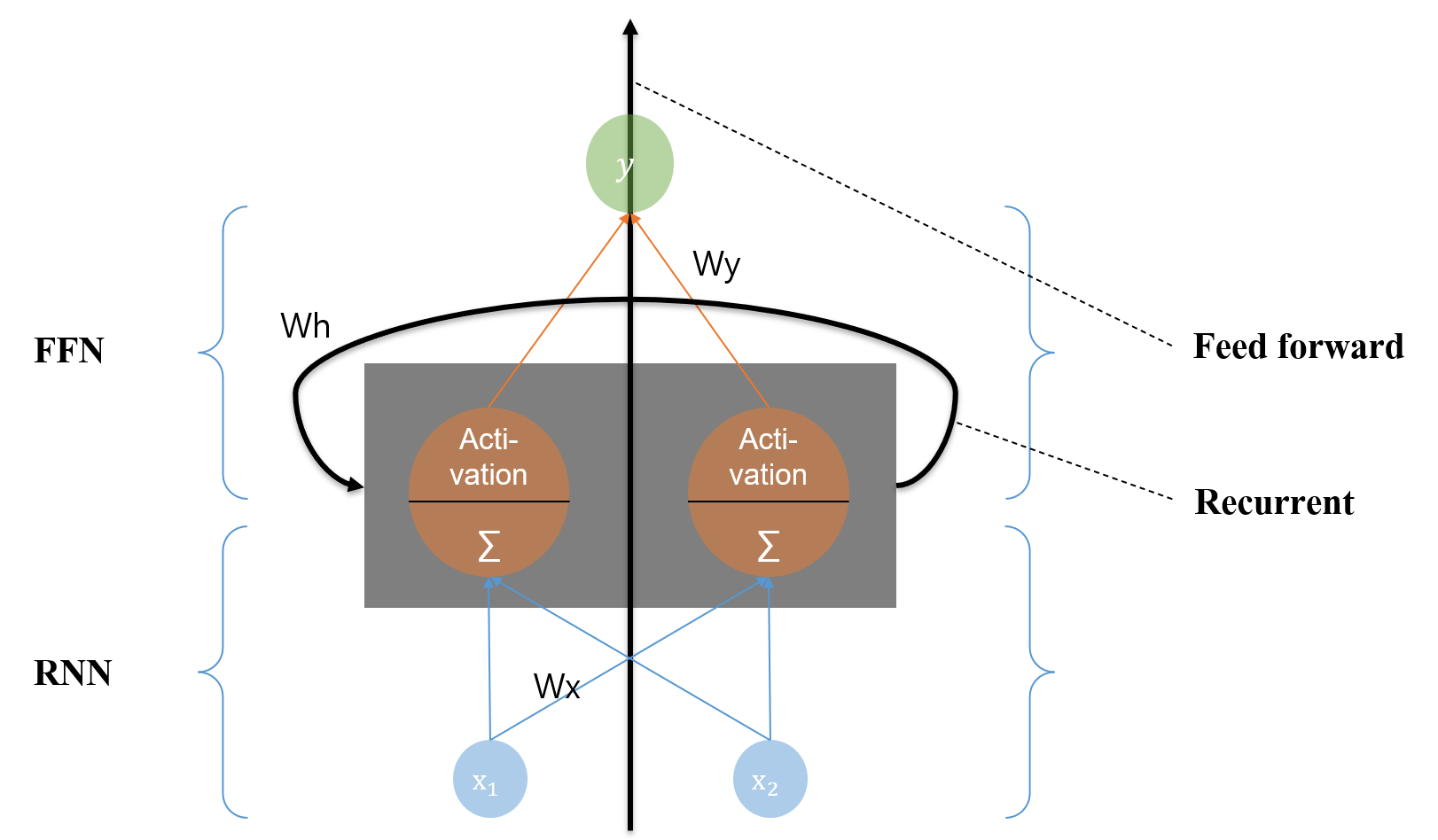
가운데 검정색으로 표현된 Hidden 층이 중요하다. 은닉층은 Feed Forward 스텝과 Recurrent 스텝으로 구성된다. 비슷하지만 아래의 그림과 같이 출력을 다시 입력으로 받는다. 입력으로 들어온 데이터를 받는다. 그리고 Hidden 층에 올라가기 전에 Wx 가중치 행렬을 이용해 계산을 한다. 여기까지는 똑같다.

이후에 흐름이 두 가지로 나누어 진다.

첫째로, 결과를 내는 Feed Forward 흐름이다. 입력값에 가중치 행렬을 통해 행렬곱 및 더한 연산 결과 값을 현재 단계에서의 상태(State)라고 하자. 이 State 값을 Output 층으로 올라가기 전에 활성화 함수에 적용해 해당 단계에서의 결과 y를 도출한다.

참고

결과 도출은 사실 RNN 신경망 유형에서 Many-to-One인지 Many-to-Many인지에 따라 달라지지만, 지금 단계에서는 일단 그 구분은 하지 않고 흐름이 두 가지로 나누어진다는 것에 집중하기 위해 이렇게 설명한다.

둘째로, 결과를 다시 입력하여 다음 단계의 계산에 활용하는 Recurrent 흐름이다. 현재 단계에서의 State 값을 다시 다음 단계의 입력으로서 활용한다. 다음 단계의 RNN 셀로 넘기는 것이다. 이를 위해 Wh라는 또 하나의 가중치 행렬 파라미터가 필요해진다.

위의 그림만으로는 이해하기 어렵기 때문에, 각각의 단계를 해체(unfold)하여 그림으로 나타내면 다음과 같다.

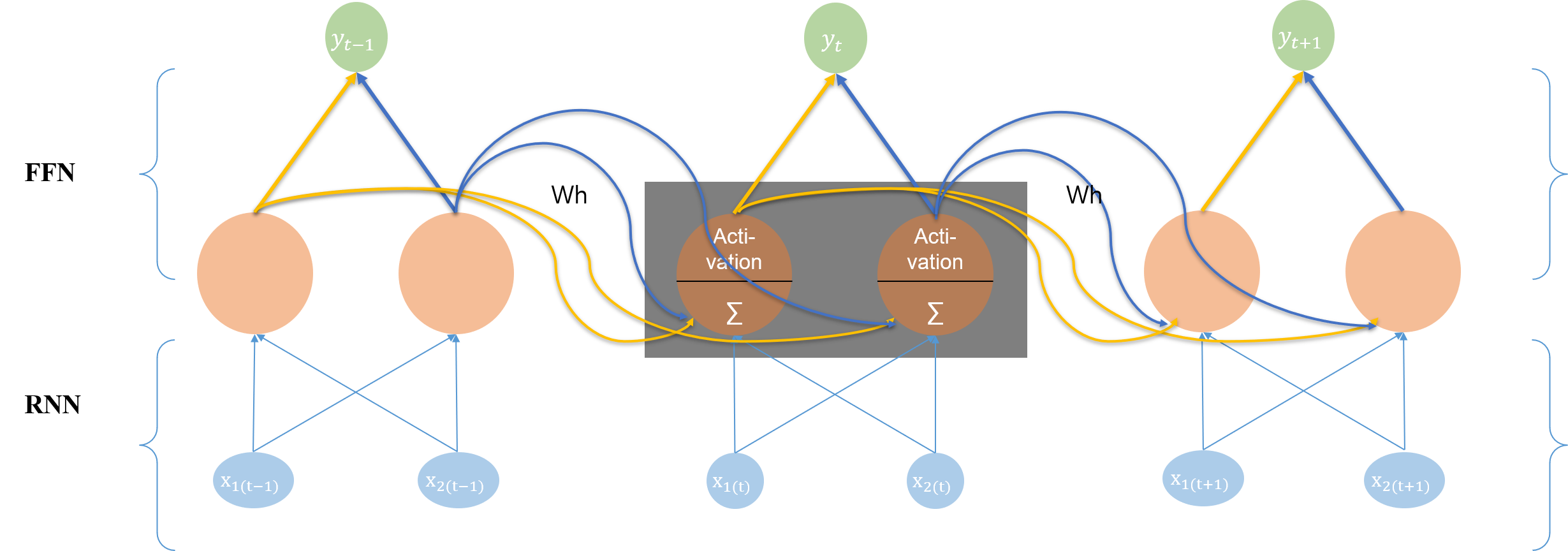
제일 먼저 기억해야 할 것은 단계별로 적용되는 W는 모두 동일하다는 것이다. 단순히 시퀀스별로 해체하여 나타낸 것에 불과하기 때문에, 위의 그림에서 Recurrent 및 Forward에 사용되는 가중치는 동일한 것이다. 이 가중치 행렬은 한 에폭의 학습이 끝나고 손실을 계산한 뒤 전체적으로 조정되는 것임에 유의하자.

그림의 흐름을 보면, 두 가지 흐름을 파악할 수 있다.

• 현재 단계에서의 상태 값이 Feed Forward Network로 입력되어 결과값을 출력하는 데에 사용된다.
• 현재 단계에서의 상태 값이 다음 Recurrent Network로 넘어 가 다음 단계의 상태를 계산하는 데에 사용된다.

이를 바탕으로 RNN 모델에서 상태 값을 계산하는 방식을 수식으로 나타내면 다음과 같다.

\[h_t = f_W(h_{t-1}, x_t)\]

f는 가중치 행렬 W로 현재 상태를 계산하는 함수이고, h는 각 단계에서의 상태 값을 의미한다. 이전 상태와 현재 상태의 입력값을 특정 함수에 적용해 현재 상태의 값을 계산해 낸다.

이렇게 현재 상태의 값을 계산하는 데 있어 RNN 모델은 Hyperbolic Tangent 함수를 사용한다. 이전 활성화 함수 강의에서도 살펴보았듯, Hyperbolic Tangent 함수는 Vanishing Gradient 문제에 상대적으로 강하기 때문에, 그래디언트를 최대한 오래 유지할 수 있도록 하기 위함이다.

2. 오류 역전파

RNN의 오류 역전파 알고리즘은 BPTT(Back Propagation Through Time)이라 한다. 명칭에서도 알 수 있듯, 시간에 걸쳐 Back Propagation을 진행하는 것이다.

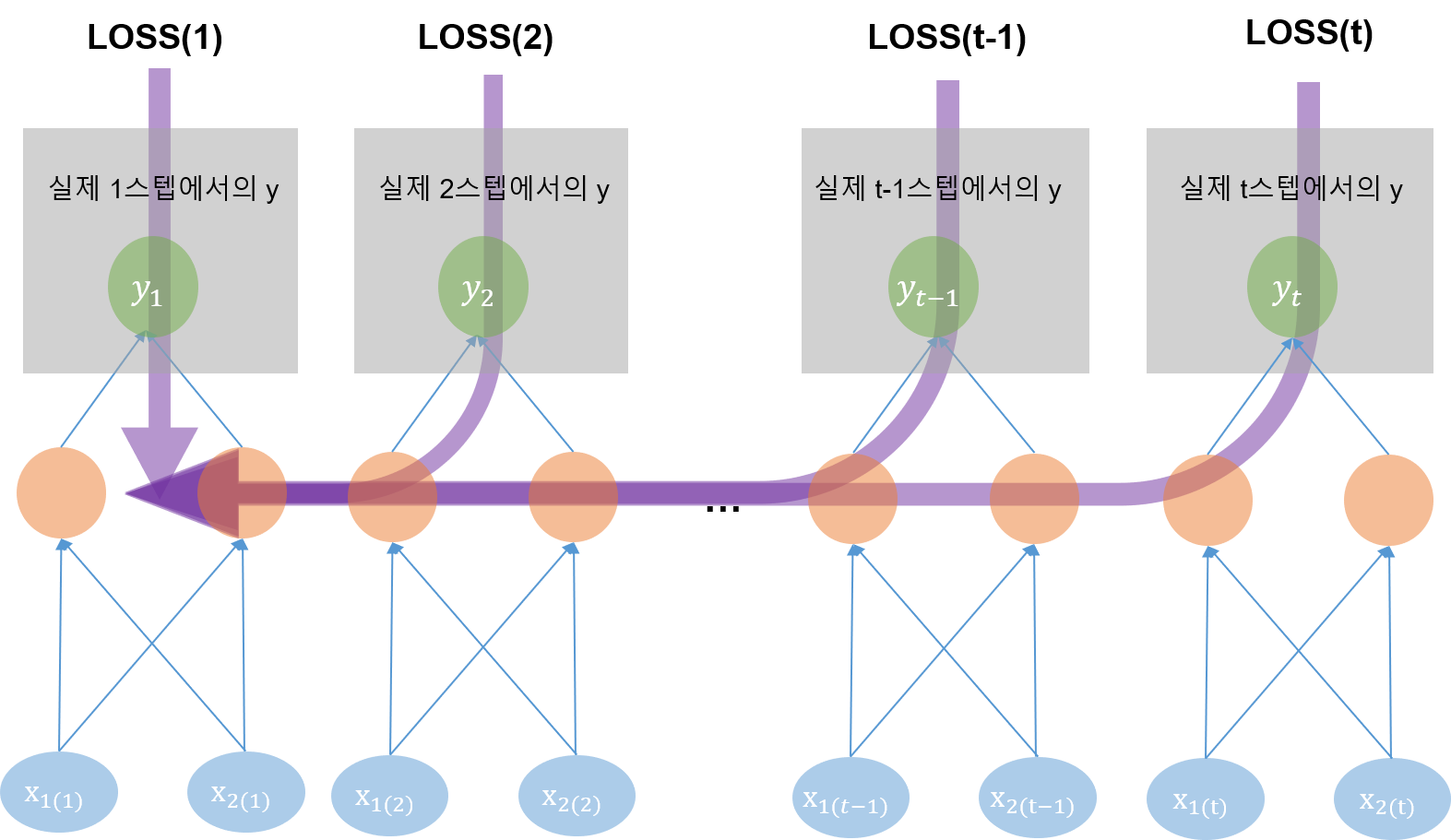
일반적인 Feed Forward Network 신경망과 달리, 각 시퀀스 스텝마다 오류를 측정해서 이전 스텝으로 전파한다. 말하자면 가중치 행렬을 조정하기 위해 계산된 loss 값의 책임을 특정 시퀀스 스텝에만 전가하는 것이 아니라, 이전의 몇 스텝에 모두 분배하는 것이다. 스텝 간 적용되는 W와 b가 모두 공통 파라미터이기 때문에 모두 분배되는 것이다.

3. 문제: Vanishing Gradients

머신러닝 모델에 학습을 시킨다는 것은 결국 학습 데이터에 맞는 가중치 행렬을 업데이트한다는 것이다. 그리고 최적의 가중치 행렬을 얻기 위해서는 loss를 계산한 뒤, 이를 역전파하는 Back Propagation 알고리즘이 제대로 작동해야 한다.

그러나 RNN 모델의 경우, 위에서 보았듯 역전파 알고리즘으로서 BPTT 방식을 사용하기 때문에, 신경망 아래단으로 뿐만 아니라, 시간의 방향으로도 역전파가 이루어진다. 따라서 chain rule을 적용해 미분을 해나가다 보면, 이전 단계로 갈수록 그래디언트가 점점 작아지는 문제가 발생한다. 말하자면, loss를 왼쪽으로 전파시킬 때 계산량이 점점 많아지고, 전파되는 양이 점점 작아지는 것이다.

이 문제를 해결하기 위해 loss를 몇 스텝까지만 전파하는 Truncated BPTT 방식을 사용할 수도 있지만, 보다 근본적으로는 이 문제를 해결한 LSTM 모델을 사용한다.