[DL] LSTM_1.모델 구조

^{조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo}

^{Tensorflow : 2.2.0}

LSTM 모델 이해하기

1. 개요

RNN 모델 의 가장 큰 문제점이 Vanishing Gradient 문제라고 했다. 이러한 문제를 해결하고자 네트워크 구조를 변경하여 고안된 모델이 바로 LSTM 모델이다.

시퀀스의 패턴을 파악하여 학습할 수 있다는 것이 RNN 모델의 장점이기 때문에, 몇 가지 파라미터를 추가하여 RNN 모델에서는 할 수 없는 일을 하도록 설계했다. 예컨대, 우리 엄마는 영국 사람입니다. 그래서 엄마의 가르침을 받은 나는 ____를 잘하죠.라는 문장에서 빈 칸을 예측할 때, 빈칸 바로 앞, 혹은 앞앞 보다 영국, 엄마 등의 단어가 더 중요할 수 있다. 그래서 RNN 모델의 Vanishing Gradient 문제를 해결하고 한참 전의 데이터까지 고려하여 학습할 수 있도록 모델을 만든 것이다.

기본 아이디어는 다음과 같다. 기존 RNN의 Recurrent 스텝에 C를 추가한다. C는 Cell State로서, 먼 과거의 기억을 얼마나 반영할지 제어하는 역할을 한다. 각각의 LSTM 뉴런 사이에서는 이전 뉴런에서의 출력 값과 이전 뉴런에서의 Cell State가 전달된다. Cell State는 h와 별개로 이전 단계를 얼마나 기억할지만을 나타내는 변수이기 때문에, 이것이 얼마나 업데이트되고 변하는지에 따라 예전의 기억을 얼마나 저장하고 반영할 것인지 조절할 수 있게 된다.

2. LSTM 네트워크 구조

RNN과 마찬가지로, chain 형태로 이전 스텝과 이후 스텝이 연결되어 있다. Recurrent 스텝을 RNN 공부할 때와 마찬가지로 펼쳐 보면 다음과 같이 전반적인 연결 구조를 이해할 수 있다.

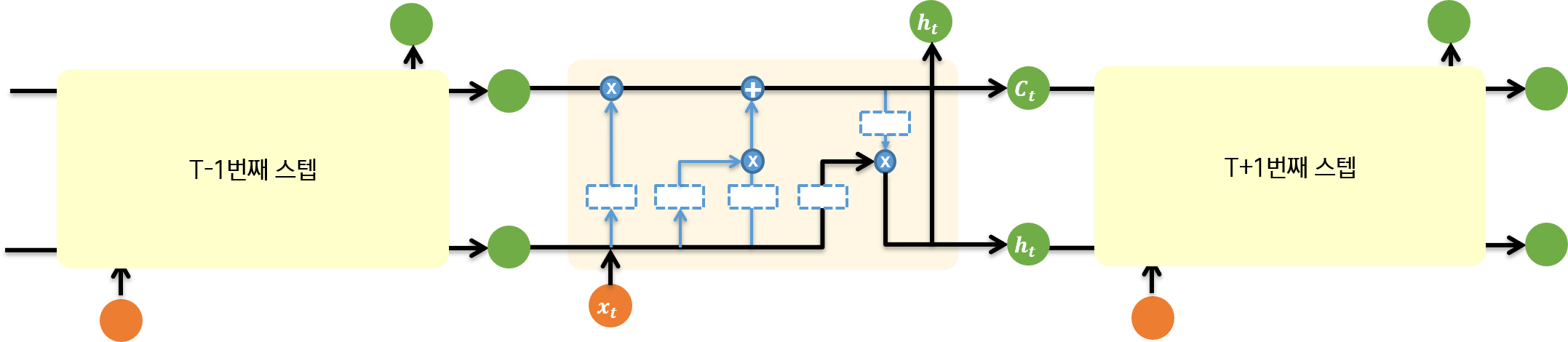
2.1. 뉴런 내부 흐름

t번째 스텝에 LSTM 뉴런 내부에서 무슨 일이 일어나는지 살펴 보자.

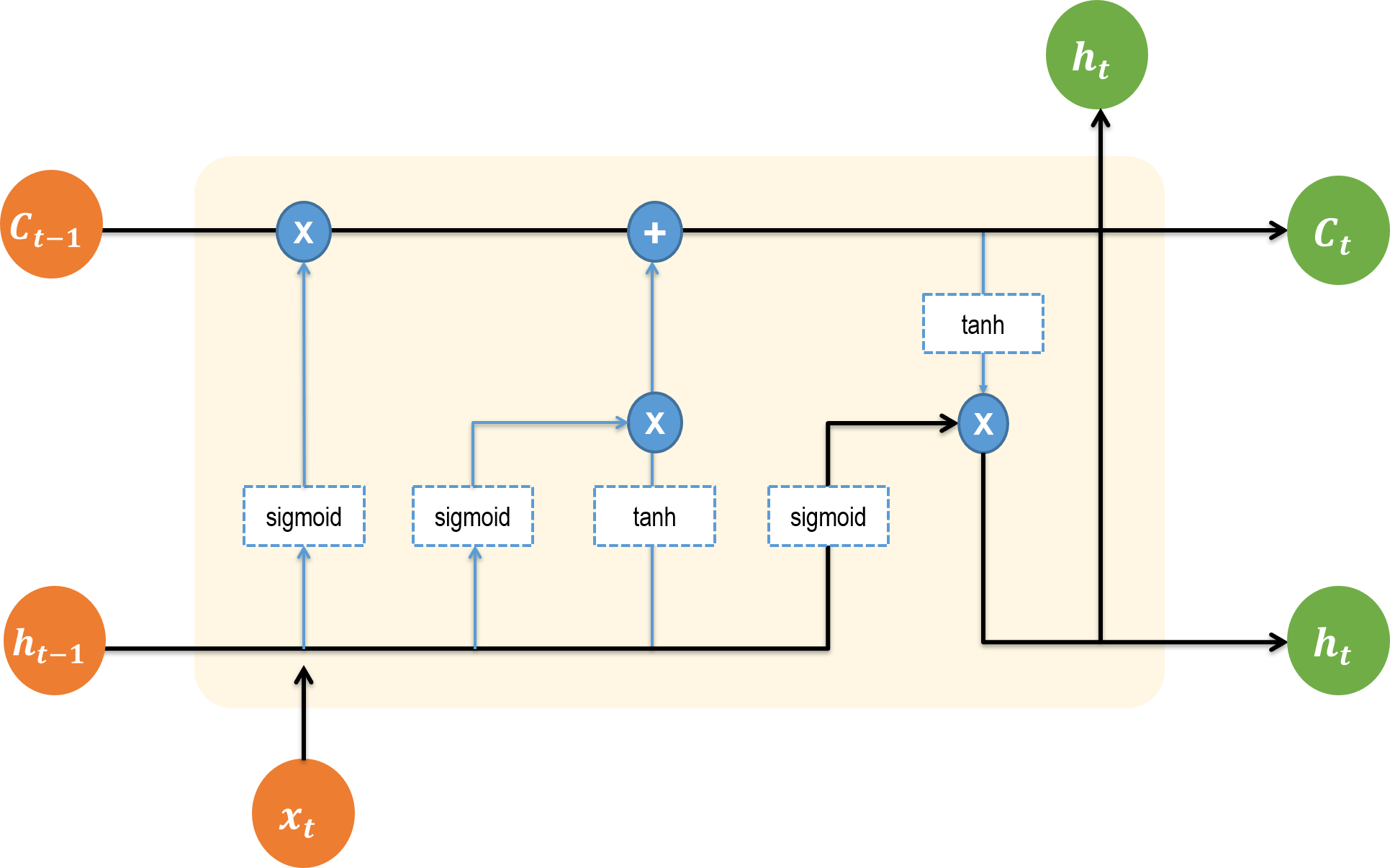
입력과 출력을 먼저 확인하자. 입력으로 들어오는 데이터는 주황색 원으로 표현했다. 입력되는 데이터는 이전 단계에서의 출력값 h와 이전 단계의 cell state인 C이다. 그리고 현재 스텝에서 출력값 사용에 활용할 데이터 x도 입력된다. 해당 뉴런에서 연산을 거치고 나면 두 가지의 출력값이 나온다. 초록색 원으로 표현된 값들이다. 현재 상태를 기억할 정도인 Cell state인 C와 현재 시퀀스 스텝에서의 출력값 h이다.

위의 입출력을 바탕으로 중요하게 이해해야 할 커다란 흐름을 검정색 화살표로 표현했다. 흐름에서 잡고 가야 할 것은 다음의 두 가지다.

• 현재 뉴런에서의 출력값은 출력값대로 나온다. 맨 위에 있는 초록색 원이다.
• 현재 뉴런에서의 출력값 h와 C는 다음 뉴런의 입력값으로 사용된다. 연결되는 맨 오른쪽 두 개의 원이다. 다음 단계의 뉴런에서는 해당 값들이 그림 왼쪽의 주황색 원이 될 것이다.

2.2 뉴런 네트워크 내부 연산

^{강사님의 강의 외에, 이 글도 참고했다.}

LSTM 뉴런의 내부 연산도 모두 네트워크 구조이기 때문에, 각각의 하위 네트워크들로 나누어 단계별로 어떤 연산이 일어나는지 톺아보자.

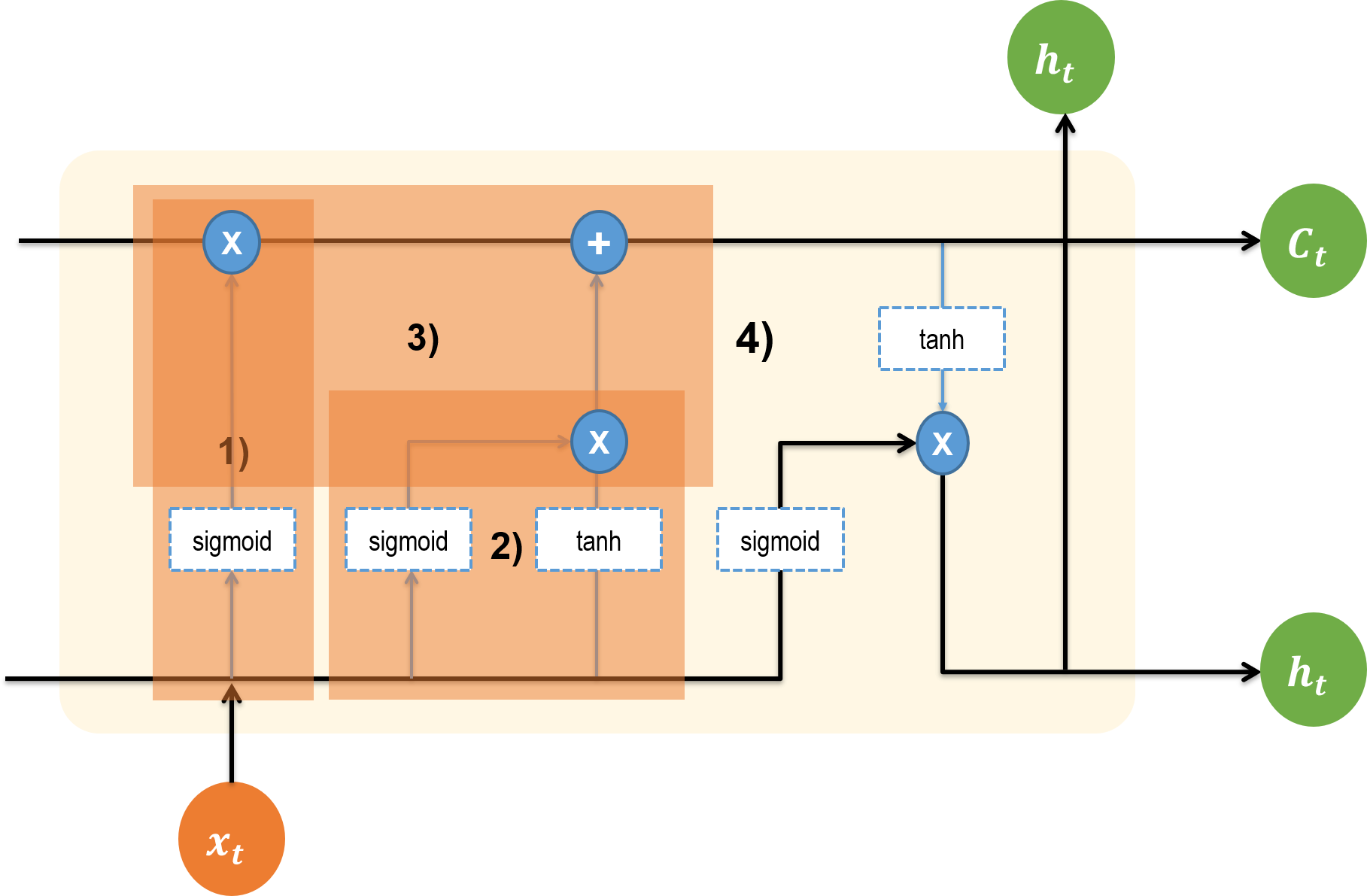
그림 설명

• 파란색 원 : 연산을 나타낸다. X는 일반적인 행렬곱이 아니라 elementwise 연산을 나타낸다.
• 파란색 사각형 : 각 단계에서의 활성화 함수이다. LSTM에서는 sigmoid와 hyperbolic tangent 함수가 사용된다.
• 파란색 화살표 : LSTM 뉴런 안의 하위 네트워크에서 결과 값들이 이동하는 흐름을 나타낸다.

1) Forget Gate: 얼마나 잊어버릴 지 결정

1)에 해당하는 부분은 입력으로 들어 온 h(t-1)이 f 함수와 만나는 지점이다. f 함수는 얼마나 잊어버릴 지를 결정하는 함수로, 다음과 같다.

\[𝑓𝑡 = 𝜎 (𝑊_f \cdot x_t + 𝑈𝑓 \cdot h_{t-1} + b_f)\\ (\sigma = Sigmoid)\]

Sigmoid 함수 안에 있는 식을 통해 잊어버릴 정도를 결정한다. 그 내용이 무엇인지 파악하는 것은 범위를 넘으므로 설명하지 않는다. (강사님 말씀에 의하면 f 안에 또 다른 파라미터가 있어서, 그 파라미터가 잊어 버릴 강도를 결정하는 역할을 한다고…)

중요한 것은 Sigmoid 함수를 취한다는 점이다. 이전 셀의 출력값을 잊어버릴 정도를 정했는데 그 값에 Sigmoid 함수를 취했으므로, 이 단계의 네트워크에서는 다음과 같은 결론을 얻을 수 있다.

“1이면 모든 정보를 일단 가져 가고 봐!”

“0이야? 그럼 갖다 버려.”

결과적으로 Forget Gate에서 활성함수로 Sigmoid를 사용했기 때문에, 그 결과가 0이면 이전의 Cell State 값이 앞으로의 모든 내부 연산에 전혀 영향을 미치지 않는다. 반대로 그 결과가 1이면 앞으로의 모든 내부 연산에 이전의 Cell State 값을 그대로 유지시킨다.

2) Input Gate: 임시 Cell State 만들기

1)과는 별개로, 해당 단계에서 들어오는 새로운 정보 중 어떤 정보를 지금 단계의 C에 저장할지 정한다. 수식으로 살펴 보면 다음과 같다.

\[i_t = \sigma (W_i \cdot x_t + U_t \cdot h_{t-1} + b_t) \\ \tilde{C}_t = tanh(W_C \cdot x_t + U_c \cdot h_{t-1} + b_c)\\\]

이전 단계에서 입력으로 받은 h 값과 지금 스텝에서 입력으로 받은 x에 각각 Sigmoid, Hyperbolic Tangent 활성화 함수를 취하고, 각각을 i, 임시 C라 하자.

3) Input Gate: 현재 Cell State 업데이트

이전 단계에서 만들어 놓은 i 와 C 값을 바탕으로 현재 스텝에서의 Cell State를 만든다.

\[C_t = (f_t ⨂ C_{t-1}) + (i_t ⨂ \tilde{C}_t)\]

1)에서 f가 얼마나 잊어버릴지를 결정하는 함수라고 했다. 이전 스텝의 출력이자 현재 스텝의 입력으로 들어 온 이전 상태의 Cell State와 f의 연산을 한다. 그렇게 해서 진짜로 이전 상태의 Cell State를 잊어 버린다(..!). 그리고 i와 2)에서 만든 임시 Cell State와 X 연산을 한다.

“forget x 예전 Cell State + input x 지금 Cell State 구조네?”

“과거 상태와 현재의 상태에 가중평균 해서 얼마나 먼 기억까지 기억해야 할지 결정한다.”

이 단계의 연산이 의미하는 바를 이해하는 것이 중요하다. 결국 1)에서 이전 스텝의 출력을 기억할지 잊을지 정했고, 2)에서 1)과는 다른 맥락으로 과거의 상황과 현재의 상황을 어느 정도 비중으로 기억할지를 결정하는 임시 cell state를 만들었다. 이후 두 값을 합해서 과거에서 현재로 넘어갈 때 어떤 정보를 얼마나 저장해야 할지를 정한다.

결과적으로 Input Gate에서는 지금의 입력과 이전의 출력으로 얻어진 값을 얼마나 현재의 Cell State 값에 반영할지 결정한다.

4) Output Gate: 현재 스텝의 출력 결정

이제 현재 뉴런에서 출력될 h 값을 결정한다.

\[O_t = \sigma(W_o \cdot x_t + U_o \cdot h_{t-1} + b_o) \\ h_t = O_t ⨂ tanh(C_t)\]

입력 값으로 들어 온 x 데이터가 가중치 행렬과 곱해지고, 그 값에 Sigmoid를 취한다. 이를 O라고 하자. 그리고 3)에서 결정한 현재 상태의 Cell State 값과 O 값에 Hyperbolic Tangent 활성화 함수를 취해 -1과 1 사이의 값을 받는다. 이렇게 얻은 두 값에 X 연산을 한다. 그 결과가 현재 스텝의 출력 h를 결정한다.

“output(-1 ~ 1) x 현재 Cell state 구조이다.”

“최종적으로 얻어진 cell state 값을 얼마나 gate에 통과시킬 때 얼마나 output에 적용해줄 지 결정하는구나!”

2.3. 요약

이러한 내부 연산 과정을 거쳐 얻은 h와 C 값을 이후 스텝에 넘긴다. Recurrent한 구조가 된다는 의미다.

(솔직히 내부 연산을 전부 다 수식적으로 이해하기는 힘들고)

• 기존 RNN 네트워크에서와 달리 더하기 연산을 사용하고,
• 활성화 함수로 tanh를 사용하여 그래디언트 소실 문제를 해결했다는 점에,

주목하자.

3. 내 마음대로 이해하기

이전의 댓글 분석 프로젝트 에서 어려움을 겪었던 댓글을 참고해서 (마구잡이로) 위의 구조를 이해해 보자.

해당 단계에서 라벨링 및 예측에 어려움을 겪었던 댓글은 다음과 같다.

사무직은 초근도 못하고, 추가 수당도 없고, ... 헬입니다.
( 중략 )
그런데 생산직은 좋겠죠.

주 52시간 근무제에 대한 댓글을 감성분석하는데, 부정으로 예측하기를 원했던 댓글이었지만, 모델이 예측한 결과는 계속해서 긍정이었다. 물론 댓글을 쓴 사람이 사무직에 종사하고 있음을 우리는 알 수 있고, 관련 정보를 모델이 학습할 수 있는 부분도 없었다.

그러나 순전히 학습 목적에서 RNN 모델이 이 문장의 뒤에 있는 정보를 중시해서 앞에 있는 정보를 잊어버린 것은 아닐까 궁금증이 생겼다. 그래서 저 댓글이 LSTM 아키텍쳐를 통과하면 어떤 식으로 예측이 나오게 될지 이해해 보기로 했다.

3.1. Forget Gate

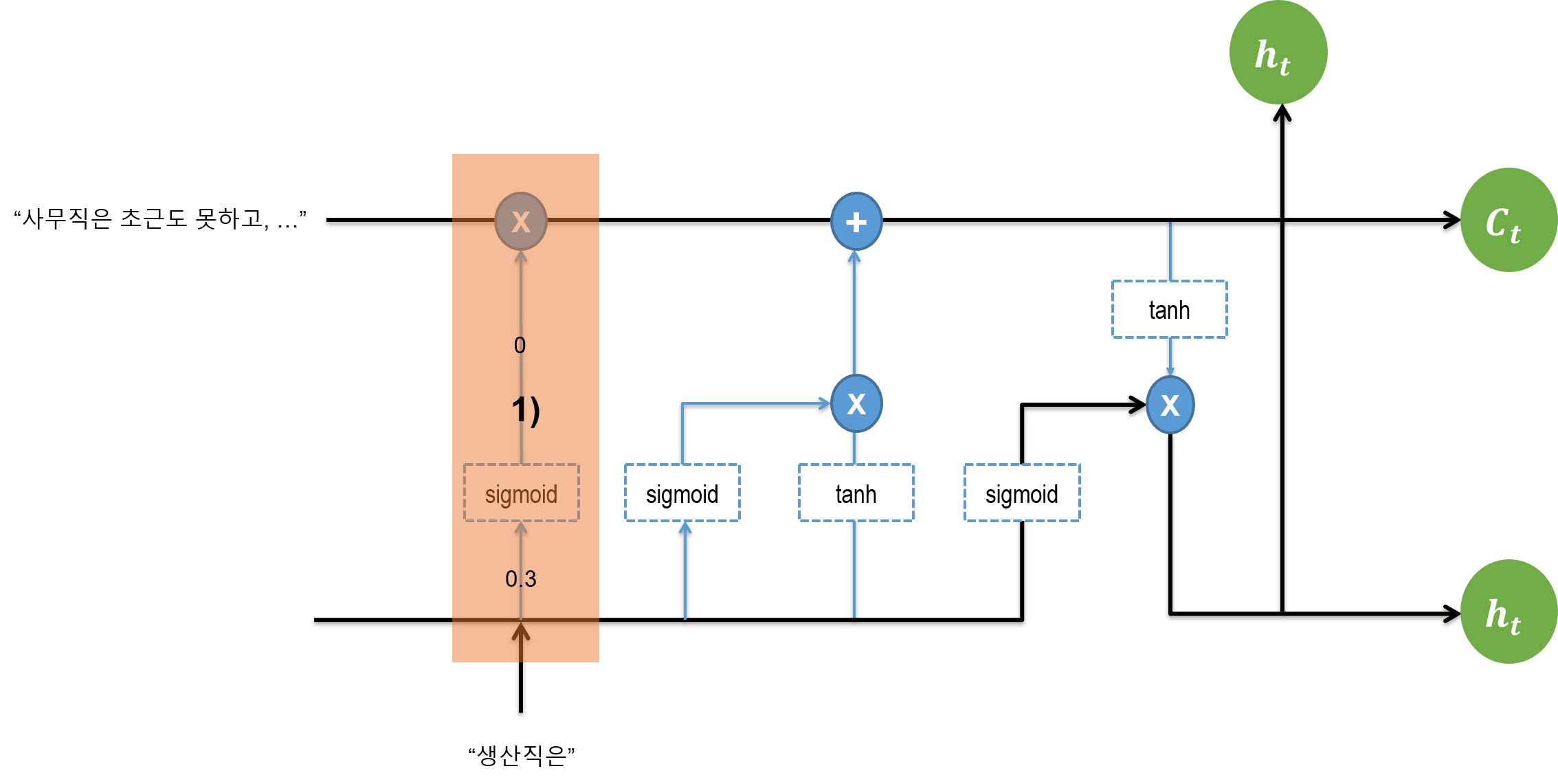
잊는 메커니즘부터 보자. 과거의 문장이 “사무직은 초근도 못하고, …＂이 이전 Cell State에 들어 있다. 이 Cell State가 입력되고, 한편으로 이전 스텝에서의 출력값 h와 , 새로운 문장의 첫 단어인 “생산직은”이 들어온다. 이전 스텝의 출력 h와 해당 스텝의 입력 간 Sigmoid를 취한 값이 0.3이 나온다고 하자. Sigmoid 값이 취해지면서 0.3은 0이 되고, 이 값이 화살표를 따라 올라간다.

이전의 cell state인 C(t-1) 값이 있다. 0이 위로 올라가면서 C(t-1)과 만나 elementwise 연산이 취해지면서 이전의 C값도 사라진다. 예전 state를 잊어버리라는 메커니즘을 수학적으로 구현한 것이다.

3.2. Input Gate

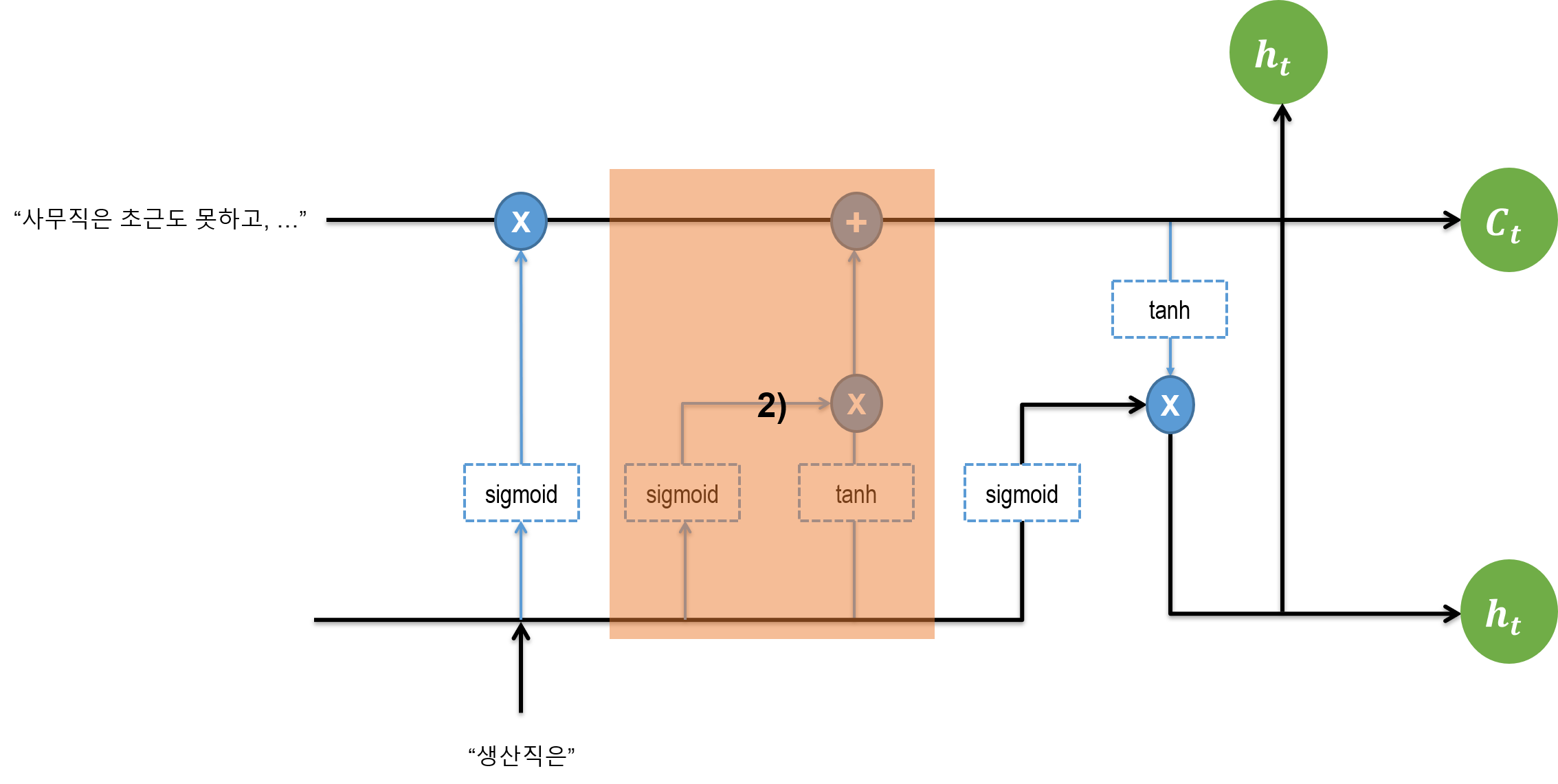
현재의 정보가 들어와서 각각 sigmoid, tanh 함수를 거친 뒤 elementwise연산이 된다. 이게 현재 정보가 된다.

이후 이게 위로 올라가면서 과거의 Cell State 정보에 더한다. 과거의 Cell State에서 넘어온 정보가 0이므로, 새로운 정보가 그대로 보존된다. 정보를 더해준다는 점이 중요하다. 곱하기 연산을 했더라면 현재 정보도 0이 되어 버린다.

3.3. Output Gate

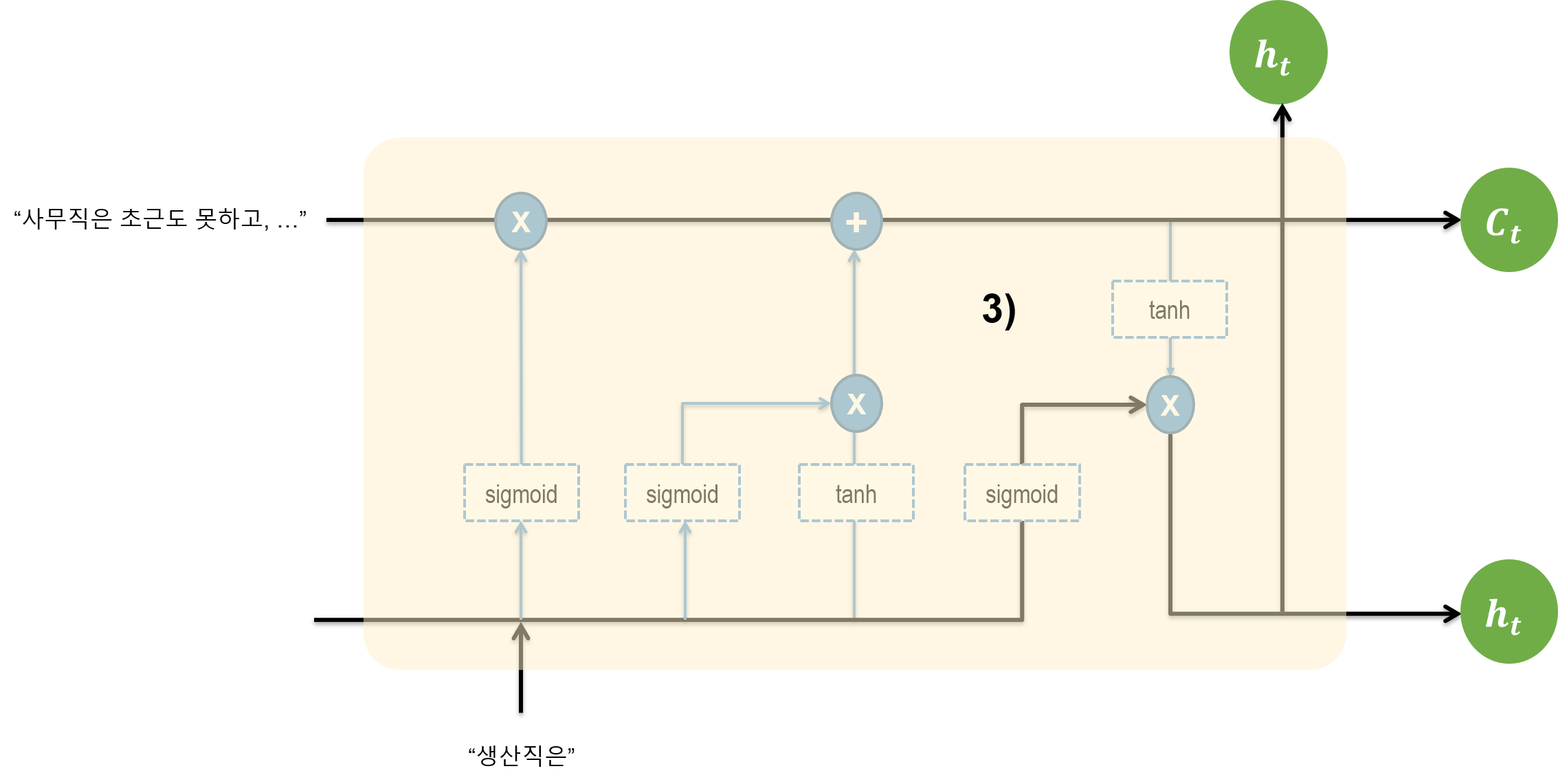
출력되는 부분을 보자. 이전 단계에서까지 더해져서 저장되어 있는 정보가 tanh 함수를 거쳐 넘어 온다. 그리고 이전 스텝에서의 h와 현재 정보가 sigmoid 함수를 거쳐 활성화 값으로 변경된다. tanh 함수를 취한 값과 sigmoid 함수를 취한 값을 서로 elementwise 연산한다. 이 값이 output이다.

-1과 1 사이의 값, 그리고 0과 1 사이의 값이 곱해지므로, 현재 셀의 값이 -1과 1 사이의 값으로 나온다. 다음 스텝으로 넘어가더라도 미분값이 sigmoid 함수보다는 크기 때문에, 그래디언트 소실 문제가 완화된다.