[DL] LSTM_3.단방향 모델 구현
출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo
Tensorflow : 2.2.0
단방향 LSTM 구현
시계열에 따른 트렌드와 노이즈를 동시에 갖는 Sine 곡선 데이터를 LSTM 모델을 활용해 예측한다.
먼저 필요한 모듈을 불러 온다.
# module import
import numpy as np
from tensorflow.keras.layers import Input, Dense, LSTM
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
1. Many-to-One
1.1. 데이터 생성
데이터 범위(X_data)와 시퀀스 길이(step)를 인자로 받아, 데이터 범위를 step 만큼 잘라 시계열 데이터를 생성하는 함수를 만든다.
함수의 반환 값은 LSTM 모델에 입력 데이터로 활용될 3차원 배열 X와 2차원 배열 Y이다.
def createData(X_data, step):
m = np.arange(len(X_data)-step)
X, Y = [], []
for i in m:
# X 데이터 생성
a = X_data[i:(i+step)]
X.append(a)
# 라벨 생성
b = X_data[i+1:(i+1+step)]
Y.append(b[-1])
# LSTM 모델 입력 형태에 맞게 변환
X = np.reshape(np.array(X), (len(m), step, 1))
Y = np.reshape(np.array(y), (len(m), 1))
return X, Y
LSTM 모델에서 텐서의 차원이 매우 중요하다.
일단 입력(Many)에 해당하는 X 데이터를 보자. 입력 형태에 맞게 변환하기 전까지, X에는 step의 크기만큼 잘려진 data가 들어가 있다. 이 데이터를 데이터의 개수를 D0 축으로, 시퀀스의 개수인 step을 D1 축으로, 숫자 1개만 있으므로 feature 수인 1을 D2 축으로 하여 3차원으로 변환한다.
출력(One)에 해당하는 Y 데이터를 보자. 입력으로 들어갈 X 데이터 각각에 대해 라벨이 한 개씩만, 데이터 개수만큼 있으면 되기 때문에 2차원으로 변환한다.
이후 Sine 함수를 생성하기 위한 X 데이터를 만든다. 기본 Sine 함수의 식을 np.sin(2 * np.pi * 0.03 * np.arange(1001))로 하여 1부터 1001까지의 X에 대해 Sine 함수의 값을 적용한 데이터를 만든다. 여기에 0.01의 기울기를 주어 우상향하는 추세를 만들고, random 모듈을 활용해 무작위의 노이즈를 더한다.
# 노이즈 포함한 시계열 sine 데이터
data = np.arange(1001)*0.01 + np.sin(2*np.pi*0.03*np.arange(1001)) + np.random.random(1001)
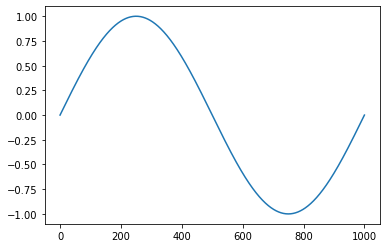
참고 : 노이즈가 없는
Sine함수기본
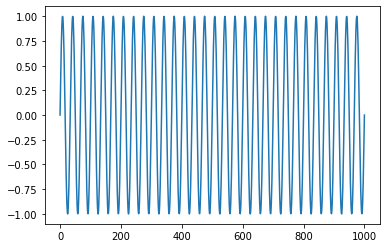
Sine함수에서 0.03을 바꿔줌에 따라 다음과 같이 그래프 모양이 변한다.
0.001 0.03 0.05 1
이후 분석할 기간의 수를 설정하고, 데이터 생성 함수에 따라 LSTM 모델에 입력으로 활용될 데이터를 만든다. 연습을 위해 분석할 step은 20으로 설정한다.
# step 수 설정
n_step = int(input('분석할 step(기간) 수를 설정하세요: '))
# 시계열 데이터 생성
x, y = createData(data, n_step)
print(f"X 데이터: {x.shape}, y 데이터: {y.shape}")
데이터의 shape을 확인하면, X 데이터의 경우 (981, 20, 1), Y 데이터의 경우 (981, 1)이다. 의도한 대로 잘 나왔다.
1.2. LSTM 모델 생성 및 학습
Keras의 LSTM 층을 활용해 모델을 생성한다. 회귀 모델이기 때문에 loss 함수로 mse를 사용한다. 옵티마이저는 Adam으로, 학습률은 0.01로 설정한다. Feed Forward Network에서 사용될 hidden neuron의 수는 (임의로) 50으로 설정한다.
# 파라미터
n_input = 1
n_output = 1
n_hidden = int(input('hidden node 뉴런 수를 설정하세요: '))
EPOCHS = int(input('학습 횟수를 설정하세요: '))
BATCH = int(input('배치 사이즈를 설정하세요: '))
# LSTM 모델
x_Input = Input(batch_shape=(None, n_step, 1))
x_Lstm = LSTM(n_hidden)(X_input)
x_Output = Dense(n_output)(x_Lstm)
# 모델 컴파일
model = Model(x_Input, x_Output)
model.compile(loss='mse', optimizer=Adam(lr=0.01))
모델 구조를 확인하면 다음과 같다.
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 20, 1)] 0
_________________________________________________________________
lstm (LSTM) (None, 50) 10400
_________________________________________________________________
dense (Dense) (None, 1) 51
=================================================================
Total params: 10,451
Trainable params: 10,451
Non-trainable params: 0
_________________________________________________________________
None
Latent Feature 확인하기
FFN의 입력으로 올라가기 위해 활용될 Latent Feature를 확인하고 싶다면, 다음의 코드를 추가하자.
# latent 모델 생성
latent = Model(x_Input, x_Lstm)
latent_feature_ex = latent.predict(x[0].reshape(1, 20, 1))
print(f"Latent Feature: {latent_feature_ex}") # 차원 (20, ) 벡터 나옴.
Latent Feature는 LSTM의 출력이자 FFN의 입력이므로, 원래의 입력 데이터를 받아 LSTM 층을 거쳐 나온 벡터가 바로 Latent Feature이다.
Latent Feature를 출력하는 모델을 같이 생성하고, .predict를 통해 결과를 확인하면 다음과 같다.
Latent Feature: [[-0.15437411 0.09811269 -0.06606248 -0.16670185 0.11857421 0.03450212
0.09432313 -0.02546505 0.07041353 -0.01460967 0.01453727 0.09675641
0.15000826 -0.15780826 -0.06214479 0.1056202 -0.09427217 -0.03775409
-0.10479715 0.0232797 0.12839638 0.11829324 -0.06036636 -0.08706245
-0.0134191 0.12812625 0.08649176 -0.04048675 -0.0753432 0.0574959
0.00338942 0.17463613 0.09240186 -0.05440873 0.05007684 0.14306481
0.08155994 0.05440356 0.0579774 0.00674061 -0.00307704 -0.08242744
-0.01699892 -0.14912902 0.07336432 0.08721713 0.00470186 0.01463581
-0.16035978 0.05487374]]
위의 feature가 FFN으로 올라가서 Dense 층을 거치게 된다.
이제 모델을 학습한다. 학습 시 X 데이터 각각은 서로에 대해 독립적이므로, shuffle=True 옵션을 준다.
hist = model.fit(x, y, epochs=EPOCHS, batch_size=BATCH, shuffle=True)
Train Loss의 변화 추이를 그려 보자. 첫 epoch에 loss가 너무 크기 때문에, epoch 1을 제외하고 다시 그려 보았다.
| 모든 epoch | epoch 1 ~ |
|---|---|
 |
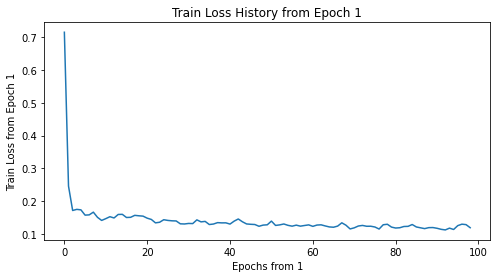 |
1.3. 예측
이제 학습된 모델을 가지고 예측하자. 예측을 위한 구조는 다음과 같다.
- 예측할 주기를
n이라고 하자. - 원래 데이터의 마지막
n주기를 가져와 그 다음 주기의 데이터를 예측한다. - 예측된 데이터를 원래 데이터에 추가한다.
- 다시 원래 데이터의 마지막
n주기를 가져와 그 다음 주기의 데이터를 예측한다.
예측하고 싶은 기간의 수치를 모두 예측할 때까지 위의 작업을 반복한다.
다만, 여기서는 데이터 개수가 너무 많기 때문에, 원래 데이터를 다 가져오지 않고, 마지막 100개의 데이터만 가져와서 예측에 활용한다. 어차피 1.2. 까지의 단계에서 모든 모델 학습이 완료되었으므로, 예측에 활용할 데이터의 수는 모델 성능과 무관하다.
예측할 미래 기간의 수를 설정하고, 예측치를 저장할 배열을 만든다. 이 때 예측치를 저장할 배열의 초깃값은, 기존 데이터의 맨 마지막 값으로 초기화한다.
# 예측 기간 설정
n_future = int(input('예측할 미래 기간 수를 설정하세요: '))
# 데이터 개수 많을 때 마지막 100일만 가져 오기
if len(data) > 100:
last_data = np.copy(data[-100])
else:
last_data = np.copy(data)
# 예측에 사용할 데이터
X_pred = np.copy(last_data)
# 예측한 애들 저장할 배열
estimate = [X_pred[-1]] # 예측 처음에 마지막 1일부터 시작하게 초기화.
참고
굳이 예측에 사용할 데이터를
copy하는 이유는, 마지막 100일 간의 데이터를 나중에 그림을 그릴 떄 활용하기 위해서이다. 그림을 그리지 않을 것이라면, 그냥 바로last_data를 사용해도 좋다.
이제 기존 데이터의 마지막 n_step만큼을 가져 와서 그 다음 데이터를 예측한다. 그리고 이것을 예측할 주기인 n_future만큼 반복한다.
반복하는 과정에서 예측된 데이터를 기존 데이터에 업데이트한다. 이 과정에서 np.insert 함수를 사용한다. 이후 예측 과정에서 이전 단계의 예측값이 활용된다.
# n_future 만큼 반복하여 예측
for _ in range(n_future):
x = X_pred[-n_step:].reshape(1, n_step, 1)
y_hat = model.predict(x)[0][0]
estimate.append(y_hat) # 추정값 저장
X_pred = np.insert(X_pred, len(X_pred), y_hat)
1.4. 결과
예측된 결과를 시각화하여 확인하자. 시각화 코드는 다음과 같다. 중간에 수직선을 긋고, 기존 데이터를 파란 색으로, 설정한 예측 기간 동안의 예측치를 빨간색으로 나타낸다.
ax1 = np.arange(1, len(last_data)+1) # 원래 데이터
ax2 = np.arange(len(last_data), len(last_data) + len(estimate)) # 예측치
plt.figure(figsize=(8, 3))
plt.plot(ax1, last_data, 'b-o', color='blue', markersize=3, label='Original Time Series')
plt.plot(ax2, estimate, 'b-o', color='red', markersize=3, label='Estimates')
plt.axvline(x=ax1[-1], linestyle='dashed', linewidth=1)
plt.legend()
plt.show()
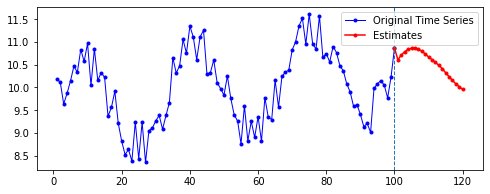
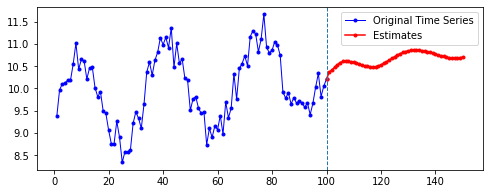
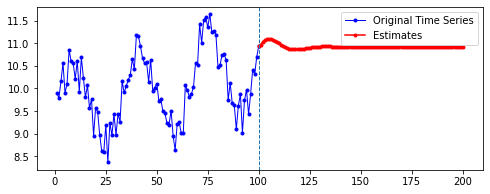
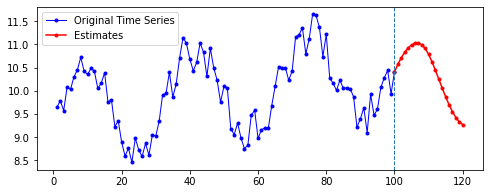
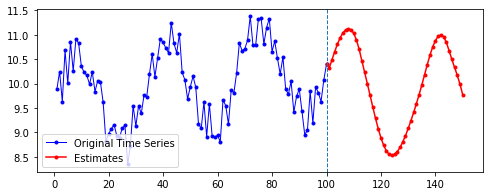
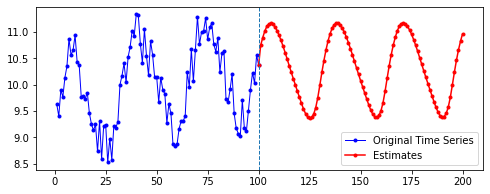
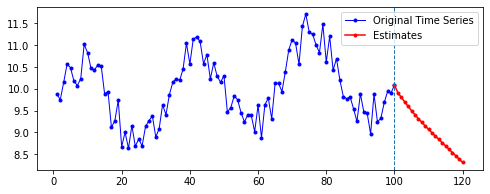
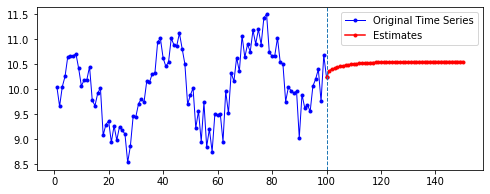
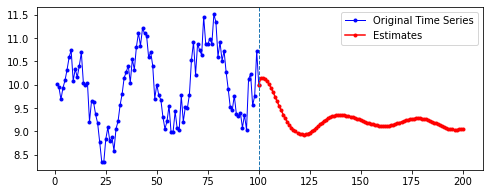
아래는 다른 파라미터를 모두 고정한 채로, 시퀀스의 길이(n_step)와 예측할 기간(n_futures)만 변경시키며 시각화한 결과를 비교한 것이다.
고정한 파라미터
n_hidden= 50EPOCHS= 100BATCH= 100
행 방향이 시퀀스의 길이, 열 방향이 예측 기간이다.
| 10 | 20 | 50 | 100 | |
|---|---|---|---|---|
| 10 | 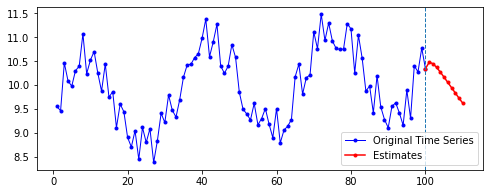 |
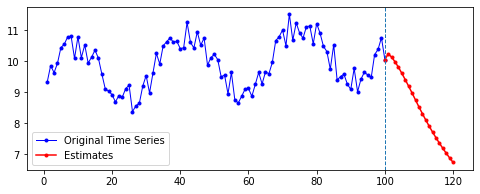 |
 |
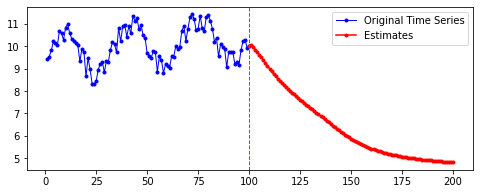 |
| 20 | 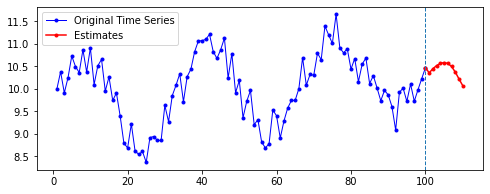 |
 |
 |
 |
| 50 | 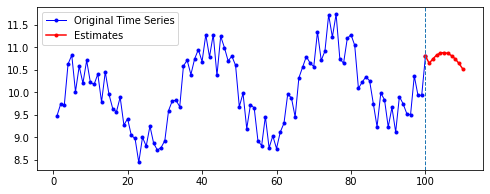 |
 |
 |
 |
| 100 | 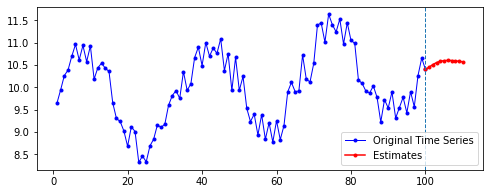 |
 |
 |
 |
아래는 개인적으로 위의 결과를 해석해본 것이다. 강사님의 지도를 받은 부분이 아니기에 틀릴 수 있다.
첫째, 공통적으로, 파란색으로 나타난 학습 데이터에 대한 패턴 예측은 Sine 함수 모양을 띤다. 그 분산이나 모양 정도에 차이가 있을 수는 있겠지만, 규칙적인 곡선 패턴 모양을 잘 보여 준다. 생각보다 별로 한 게 없는데도 잘 예측하는 모습이다.
둘째, n_step에 따라 열 방향으로 보면, 해당 n_step에서는 모양이 비슷비슷하게 나타나는 것 같기도 하다. 그런데 확실히 n_step이 커질수록 패턴이 더 규칙적이고 안정화되게 형성된다.
셋째, 확실히 파란색보다는 빨간색으로 나타난 예측 데이터의 패턴이 다르다.
확실히 n_step의 길이가 작을수록 이후 데이터 예측이 직전(혹은 최근)의 패턴에 영향을 많이 받는 듯하다. n_step이 클수록 이전의 데이터에 대해 규칙적으로 학습했기 때문인 것으로 보인다.
이것이 꼭 좋은지는 모르겠다. 예컨대, 주식 시장 상황을 생각해 보자. 잡음 제거하고, 추세 잘 예측해서 너무나도 규칙적인 패턴을 얻고, 그 결과를 바탕으로 주가를 예측할 수 있을 것이다. 그런데 예상치 못한 잡음(지금의 코로나처럼)이 생긴다면, 꼭 n_step을 길게 잡아서 규칙적인 패턴을 학습하는 것만이 좋다고 볼 수는 없을 것이다. (어떻게 보면 자기 예전 데이터에 너무 과적합되는 것이라고도 할 수 있을 것 같다)
위와 관련해 한 가지 더 생각할 수 있는 것은, 애초에 데이터를 구성할 때 (1.1. 단계) 잡음과 추세를 어떻게 설정하느냐에 따라 달라질 수도 있을 것 같다. 그런데 또 여기에 대해 너무 모델링을 하다 보면, 그것은 머신러닝의 LSTM 분석이라기 보다는 통계학적인 시계열 분석 모델링이 되어버리지 않을까 싶기도 하다.
넷째, n_futures가 n_step보다 클 때(표로는 대각선을 기준으로 오른쪽 위를 보면 된다. 예컨대 내가 학습한 시퀀스 길이보다 예측해야 할 시퀀스 길이가 더 긴 경우이다.)는 모델의 예측값이 자신의 예측값에도 영향을 받는 것으로 보인다.
요컨대, 예측해야 할 시퀀스의 길이가 자신이 학습한 시퀀스 길이를 넘어가는 순간부터는 자기 자신이 예측한 데이터에도 영향을 받는 것이다. 시퀀스 학습 길이보다 예측해야 할 패턴의 길이가 더 길기 때문에, 예측을 위해 자신의 예측값을 활용해야 한다. 이런 경우라면, 기존에 학습한 패턴이 더 규칙적일 수록 더 규칙적이고 전체 패턴에 맞는 예측이 나올 수도 있을 것이라 보인다. 기존의 패턴이 규칙적이면, 예측 패턴 역시 규칙적일 수밖에 없기 때문이다.
+) 첨언
위의 해석이..
n_step= 100인 경우를 추가하기 전까지는 그럴 수 있다고 생각하고 해석한 것이었는데, 복습하면서n_step이 100인 경우를 다시 그려 보니 전혀 맞지 않는 측면이 있는 것 같다(ㅇ_ㅇ..) 내일 다시 강사님께 질문하고 혜안을 얻어야 겠다.
+) 추가
강사님께 여쭤본 결과, 확실하게 꼬리가 길게 쳐진 것은 좀 잘못된 것이라고 하신다. 단순히
n_step,n_futures의 문제가 아니라 파라미터를 고정시켜 놓고 보다 보니,n_step,n_futures를 변화시킬 때 다른 파라미터도 함께 변화시켜서 모델 최적화시켜야 하는데, 그게 간과되었을 수도 있다고.결과 해석에 있어서는 크게 의미 부여하지 말고, 어느 정도 규칙적으로 패턴이 형성된 것을 보아야 한다. 어느 정도 규칙적으로 나온 패턴도 처음에는 구불구불하다가 나중에 패턴이 달라지게 된다. 예측값을 바탕으로 이후의 예측을 하다 보니, 이전 예측 단계에서의 오차가 계속 전파된다.
지금 단계에서 시계열 패턴을 예측하고 해석하는 데에 너무 공들이지는 말고 큰 개념을 가져 가자.
2. Many-to-Many
위의 코드에서 몇 가지 부분만 달라진다.
첫째, 데이터 생성 함수가 변한다. 이제는 X 데이터의 시퀀스를 이루는 각각에 대해 Y 라벨 값이 나와야 하므로, Y 데이터 역시 3차원이 된다.
둘째, 모델 layer 설정이 달라진다. return_sequences = True 옵션과 TimeDistributed 함수가 추가되었다. 둘을 추가하면, LSTM이 Many-to-Many 방식으로 작동한다.
전체 결과 해석 등을 위와 같은 방식으로 하지는 않는다. 다만 전체 코드를 올려 놓고, 1) 전체 코드 흐름을 파악하고, 2) 추가된 옵션이나 바뀐 부분이 의미하는 것이 무엇인지 파악하는 데에 더 주안점을 둔다.
바뀐 부분의 의미를 naive하게 설명하면 다음과 같다.
-
return_sequences = True: 중간 단계마다 모두 sequence들을 반환한다. 그러면 LSTM 뉴런이 중간 값을 모두 포함하고 있다.Many-to-One방식에서는return_sequences=False가 default로 설정되어 있다. -
TimeDistributed: 각 단계마다 Feed Forward 네트워크를 모두 둔다. 각 시간축마다 모두 feed forward 네트워크를 작동시킨다.위와 같이 중간 중간에 나와야 할 y값을 알려주어야 중간 단계마다 모두
Feed Forward네트워크가 작동할 수 있다. 이를 위해 데이터 생성 함수를 바꿔준 것이다.
이제 전체 코드를 확인해 보자.
# module import
from tensorflow.keras.layers import Dense, Input, LSTM, TimeDistributed
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
import numpy as np
import matplotlib.pyplot as plt
def createData(X_data, step):
m = np.arange(len(X_data) - step)
x, y = [], []
for i in m:
a = X_data[i:(i+step)]
x.append(a)
b = X_data[i+1:(i+1+step)]
y.append(b) # 바뀐 부분
X = np.reshape(np.array(x), (len(m), step, 1))
Y = np.reshape(np.array(y), (len(m), step, 1)) # 바뀐 부분
return X, Y
data = np.arange(1001)*0.01 + np.sin(2 * np.pi * 0.03 * np.arange(1001)) + np.random.random(1001)
# parameters
n_input = 1
n_output = 1
n_step = int(input('분석할 step(기간) 수를 설정하세요: '))
n_hidden = int(input('hidden node 뉴런 수를 설정하세요: '))
EPOCHS = int(input('학습 횟수를 설정하세요: '))
BATCH = int(input('배치 사이즈를 설정하세요: '))
# 시계열 데이터 생성
x, y = createData(data, n_step)
print(f"X 데이터: {x.shape}, y 데이터: {y.shape}")
# LSTM 모델 생성
x_Input = Input(batch_shape=(None, n_step, 1))
x_Lstm = LSTM(n_hidden, return_sequences=True)(x_Input) # 바뀐 부분
x_Output = TimeDistributed(Dense(n_output))(x_Lstm) # 바뀐 부분
model = Model(x_Input, x_Output)
# latent feature 확인
latent = Model(x_Input, x_Lstm)
latent_ex = latent.predict(x[0].reshape(1, 20, 1))
print(f"Many-to-Mant Latent Feature: {latent_ex}")
model.compile(loss='mse', optimizer=Adam(lr=0.01))
print(model.summary())
# 학습
hist = model.fit(x, y, epochs=EPOCHS, batch_size=BATCH, shuffle=True)
# plot history
plt.figure(figsize=(8, 4))
plt.plot(hist.history['loss'])
plt.title('Train Loss History')
plt.xlabel('Epochs')
plt.ylabel('Train Loss')
plt.show()
# 처음에 너무 loss 커서 빼고 그린다.
plt.figure(figsize=(8, 4))
plt.plot(hist.history['loss'][1:])
plt.title('Train Loss History from Epoch 1')
plt.xlabel('Epochs from 1')
plt.ylabel('Train Loss from Epoch 1')
plt.show()
# 예측 기간 수
n_future = int(input('예측할 미래 기간 수를 설정하세요: '))
if len(data) > 100:
last_data = np.copy(data[-100:])
else:
last_data = np.copy(data)
X_pred = np.copy(last_data)
# 예측값 저장 배열
estimate = [X_pred[-1]]
# n_future 기간 만큼의 예측
for _ in range(n_future):
x = X_pred[-n_step:].reshape(1, n_step, 1)
y_hat = model.predict(x)[0][-1][0] # 바뀐 부분
estimate.append(y_hat)
X_pred = np.insert(X_pred, len(X_pred), y_hat)
# plot
ax1 = np.arange(1, len(last_data)+1)
ax2 = np.arange(len(last_data), len(last_data) + len(estimate))
plt.figure(figsize=(8, 3))
plt.plot(ax1, last_data, 'b-o', color='blue', markersize=3, label='Original Time Series', linewidth=1)
plt.plot(ax2, estimate, 'b-o', color='red', markersize=3, label='Estimates')
plt.axvline(x=ax1[-1], linestyle='dashed', linewidth=1)
plt.legend()
plt.show()
모델 구조를 확인하면 다음과 같다.
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) [(None, 20, 1)] 0
_________________________________________________________________
lstm_2 (LSTM) (None, 20, 50) 10400
_________________________________________________________________
time_distributed_2 (TimeDist (None, 20, 1) 51
=================================================================
Total params: 10,451
Trainable params: 10,451
Non-trainable params: 0
2.1. Latent Feature
(1, 20, 50) 형태의 Latent Feature가 Feed Forward 네트워크로 전달된다.
1차원으로 평활화된 벡터가 각 시퀀스마다 20개가 있다. 그리고 그것이 hidden neuron의 수만큼 존재한다.
[[[-9.25148465e-03 2.40807571e-02 4.11372073e-03 -3.08826379e-03
-1.34491650e-02 -3.41277313e-03 7.62031833e-03 -8.08595680e-03
1.16554992e-02 1.68455914e-02 1.88495149e-04 -2.30593663e-02
3.13225342e-03 -2.17099600e-02 -2.39688400e-02 1.60198156e-02
-2.57393178e-02 -8.14876799e-03 -1.92884367e-03 2.39006002e-02
2.29536835e-03 1.78462565e-02 1.94627307e-02 1.92031171e-02
2.35425308e-03 -8.14874377e-03 -2.24701185e-02 1.31234620e-02
1.55245094e-02 1.26299858e-02 -2.19104299e-03 -3.76234623e-03
2.62713619e-02 3.30625684e-04 2.60724017e-04 2.39332914e-02
-7.89631531e-03 -1.18797254e-02 -1.44105516e-02 -2.11090110e-02
-2.38088891e-02 9.61423284e-05 -8.53901822e-03 -2.33045202e-02
-1.40177850e-02 7.36078434e-03 1.97146405e-02 7.30795506e-03
1.61902774e-02 2.07320731e-02]
...
[ 2.42188349e-02 9.41959321e-02 -9.54313055e-02 1.36666661e-02
2.87160967e-02 -5.24720550e-02 4.43686619e-02 1.66658945e-02
-1.69516597e-02 5.36630750e-02 6.01577424e-02 -1.06316186e-01
-1.97960623e-03 -1.38270184e-01 -2.58456543e-02 4.59064841e-02
-1.00109704e-01 -2.69792248e-02 -5.92217073e-02 1.43015683e-01
-5.04165469e-03 7.05343559e-02 7.70838261e-02 1.31910563e-01
-2.85066036e-03 -5.18555753e-02 -1.17357098e-01 2.91179530e-02
7.37582818e-02 -5.94193414e-02 -1.72935869e-03 -5.33339307e-02
4.59628813e-02 -3.78671288e-02 -2.63924897e-02 1.26934960e-01
-5.99848293e-03 2.82309651e-02 -9.85971987e-02 -8.84828866e-02
-1.42655551e-01 2.94372234e-02 -7.79921785e-02 -1.69591099e-01
-9.54225808e-02 6.44402653e-02 1.12806130e-02 -6.28129318e-02
1.36089191e-01 9.24586430e-02]]]
2.2. TimeDistributed
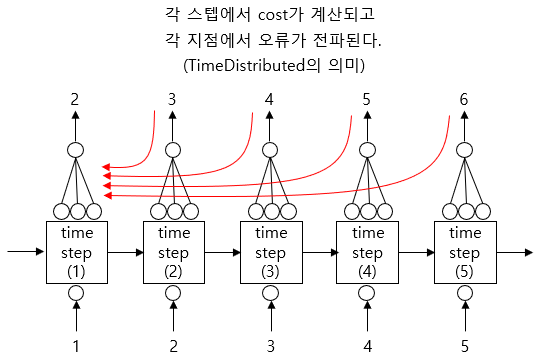
기본적으로 TimeDistributed 함수는 각 스텝마다 cost를 계산해서 하위 스텝으로 전파하여 가중치를 업데이트하는 역할을 한다. 다시 말해, 그것을 사용하지 않았을 때, 즉, Many-to-One 방식에서라면 마지막 단에서 한 번에 계산되었을 오류를 각 시퀀스 단계로 분배시키라는 의미이다.
각각의 sequence input에 대해서 결과를 돌려 주고, 각 출력(Many)별로 cost를 계산하겠다는 게 Many-to-Many 방식이 의도하는 계산 과정이다.
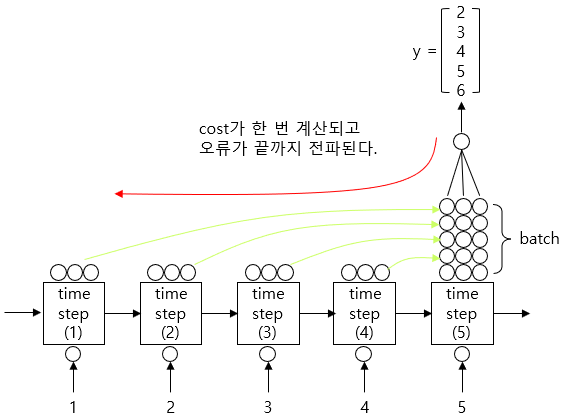
TimeDistributed 함수를 사용하지 않아도 모델이 돌아 가기는 한다. 모델의 구조를 파악하면 쉽게 알 수 있다.
그러나 의미가 달라진다. 각 sequence에 대한 각각의 출력 결과가 나오는데, 마지막에 다 몰려 버린다. return_sequences=True로 인해 LSTM의 중간 출력이 모두 사용되지만, TimeDistributed()가 사용되지 않았기 때문에 오류가 시간 축으로 분산되지 않는다. 이 경우, 모든 중간 출력에 대해 마지막 스텝에서 cost가 계산되고, 마지막 스텝에서부터 계산된 오류가 전파된다.
강사님의 자료를 참고하자.
| 잘된 사용 | 잘못된 사용 |
|---|---|
 |
 |


댓글남기기