이레이저

이레이저

[DL] CNN_1.개념 (확장)

7 분 소요

 출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo

Tensorflow : 2.2.0

CNN 모델 개념

CNN 모델의 주요 개념 은 이전에 문쌤이랑 공부할 때 한 번 훑어 보았기 때문에, 추가하여 배운 내용을 위주로 CNN을 다시 이해해 보자.

1. 주요 개념 추가

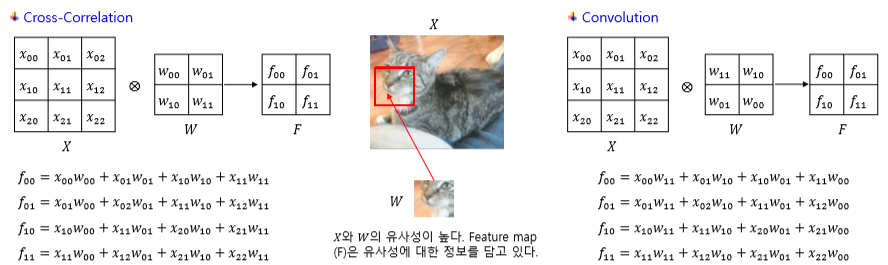
  • Convolution을 통해 생성된 Feature Map은 입력 데이터(이미지) X와 가중치 행렬 W 간의 내적과 같은 개념이(라고 한)다. 두 벡터의 내적은 두 벡터의 상관성과 밀접한 관계가 있으므로, 서로 겹치는 부분일수록 Convolution 값이 크고, 이미지와 필터 간 상관성이 높다.
  • 알고 보니, Convolution은 Filter가 뒤집힌 상태를 적용한다. Tensorflow의 Convolution은 계산의 용이성을 위해 Cross-Correlation 방식을 사용한다고 한다(…!). 계산 원리 자체는 비슷한 듯하다.

image-20200716133841614


  • Pooling layer은 non-trainable layer로서 down sampling을 하기 위한 크기만 지정한다. 데이터 소실의 우려도 있지만, 반대로 입력 데이터의 특정 부분이 약간 틀어지거나 위치가 변하더라도 동일한 결과를 얻기 위해 사용한다. 고양이 코의 위치가 달라져도 고양이 코라고 인식할 수 있다. 이미지의 일부분이 변형되더라도 그 특징을 통해 정상적으로 인식할 수 있는, 시각 불변성 특성을 보존하기 위해서이다.
  • Feature Map의 벡터들은 특징이 추출되어 원본 데이터의 잠재된 특징을 내재하고 있는 Latent Feature로 볼 수 있다.

2. CNN 네트워크와 데이터 구조

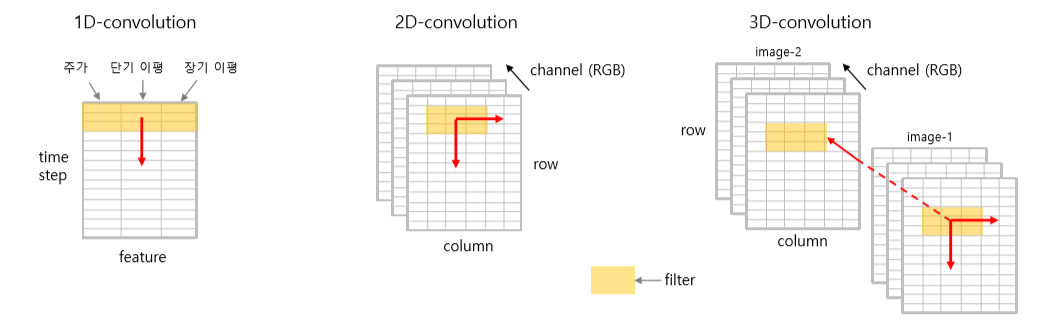
image-20200716135039164

Tensorflow에 구현되어 있는 Convolution 함수를 보면 1D, 2D, 3D 등 차원이 붙어 있다. 이는 Filter가 이동하는 차원을 나타낸다. Filter의 이동에 따라 데이터의 shape을 맞춰 주는 일이 매우 중요하다.

  • 1D Convolution : (batch, time-step, feature)

Filter가 한 방향으로 이동한다. 시계열, 음성, 문장 등 한 방향으로 이동하면 되는 데이터의 경우 사용한다. 지난 시간에 배운 RNN, LSTM 등과 동일한 구조이다. 입력 데이터의 shape은 3차원이다.

  • 2D Convolution : (batch, row, column, channel)

Filter가 두 방향으로 이동한다. 이미지 한 장 등과 같은 데이터에 사용한다. 입력 데이터의 shape은 4차원이다.

  • 3D Convolution : (batch, dim1, dim2, dim3, channel)

Filter가 세 방향으로 이동한다. 동영상 한 부분, 이미지 여러 장 등과 같은 데이터에 적용한다. 필터의 이동 방향에 time 축이 추가된다. 참고로, 컬러 이미지의 경우는 필터의 채널이 3일 뿐, 세 방향으로 이동하는 것이 아니다. 입력 데이터의 shape은 5차원이다.

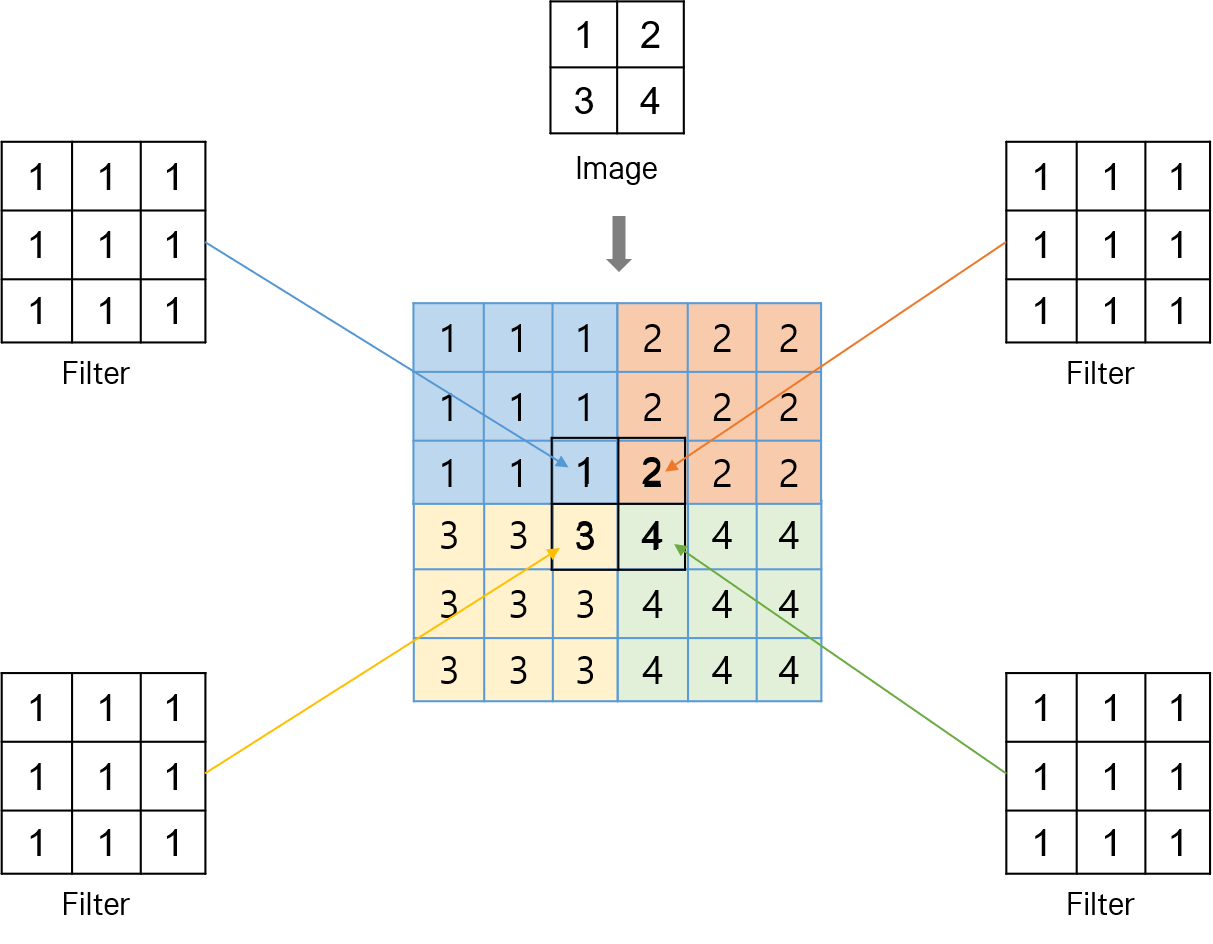
3. 오류 역전파 알고리즘

일반적인 다중 레이어 인공신경망의 back propagation 알고리즘과 크게 다르지 않다. 아래 그림과 같이 3x3 이미지 데이터에 2x2 필터를 적용해 2x2 Feature Map을 생성하는 네트워크를 생각해 보자.

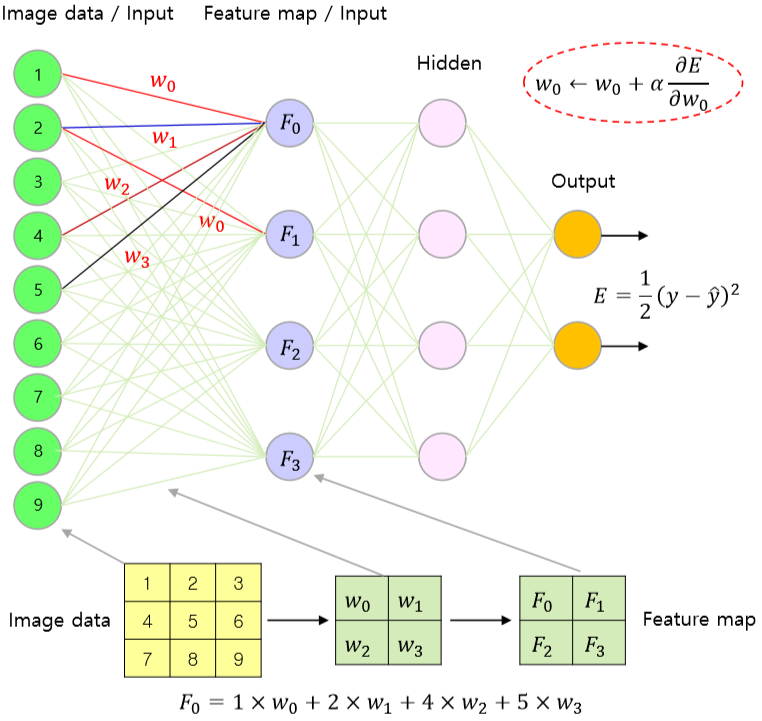
image-20200716140519522

Convolution하여 Feature Map을 생성해 내는 과정 자체를 레이어 간 connection으로 보고, 최종 output layer에서의 에러에 chain rule을 적용하여 Convolution Layer까지 에러를 역전파한다.

4. Upsampling

이미지의 차원을 줄이는 것이 아니라, 반대로 늘려주는 방법이다. Transposed Convolution이라고도 한다. 고정된 값 필터를 사용할 수도 있고(이 경우, 해당 레이어는 non-trainable layer가 된다.), Convolution 레이어처럼 weight와 bias를 설정하여 학습 가능하게 만들 수도 있다.

이전까지의 Convolution, Pooling 등이 모두 차원을 줄여 특정 부분의 feature를 강조하고, 계산 속도를 빠르게 하기 위한 Downsampling이었다면, Upsampling은 원래 이미지 크기로 복원하고 싶은 경우 사용한다. 단, 이미 소실된 feature나 유실된 데이터를 복원할 수는 없다. 이후 배울 AutoEncoder 모델에서 유용하게 사용될 것이므로 그 작동 원리를 잘 기억해 두자.

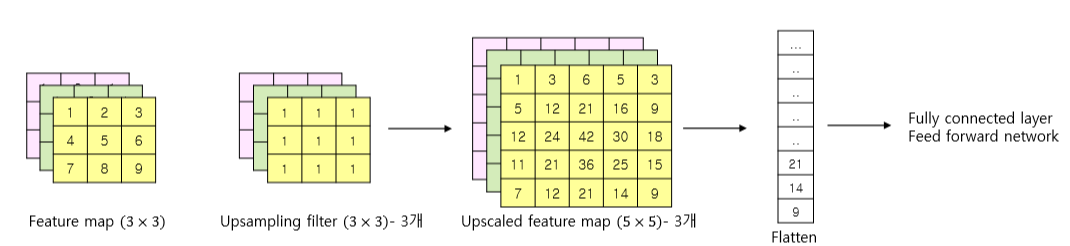
image-20200716141546360

아래 엑셀 실습 파일의 이미지를 통해, upsampling을 거쳤음에도 불구하고 원래의 입력 이미지가 변형되었음을 확인하자.

image-20200716141805047

5. 코드 구현


0713 추가 : Conv2DTranspose 작동 원리

오토 인코더 강의 때 집단 지성으로 Tensorflow에서 Transposed Convolution이 어떻게 작동하는지 알아 냈다! 유레카!

2차원 Conv2DTranspose를 예로 들어 결과가 어떻게 도출되는지 살펴보자. 중점적으로 알아보고자 하는 것은 다음의 2가지이다.

  • stride 크기의 의미
  • padding 옵션과 stride 크기의 관계

차원이 축소된 원래의 이미지에 3 x 3 크기의 1로 구성된 고정 값 필터를 적용해 upsampling한다고 하는 상황을 가정하자. 해당 필터를 원래 이미지 한 칸씩을 적용해 가며 map (정확한 용어를 모르겠다) 을 만든다.

stage1

이제 이 상태에서 stride 크기를 2로 한다. 각각의 map을 1번 map, 2번 map, 3번 map, 4번 map이라고 한다. 1번 map에서 2칸을 이동해 2번 map을 겹치고, 아래 쪽으로 내려가 1번 map에서 2칸을 이동해 3번 map을 겹친다. 이제 3번 map에서 오른쪽으로 2칸을 이동해 4번 map을 겹친다. 그러면 아래와 같이 가운데 십자가 부분이 겹친 map을 얻을 수 있다.

stage2

여기서 padding으로 SAME 옵션을 주면 transpose 결과 이미지가 원본 이미지의 stride 배가 되라고 하는 의미이다. 따라서 결과 이미지가 4 x 4 크기가 되도록 이미지를 끝에서부터 자르고, 겹친 부분은 더한다.

반면 padding으로 VALID 옵션을 주면, transpose 결과 이미지를 그대로 두라는 의미이다. 가운데 겹쳐진 숫자를 더하는 것은 마찬가지이다.

만약 stride를 3으로 준다면 어차피 각각의 필터를 적용해 map을 적용한 뒤 3칸을 이동하기 때문에 겹치는 부분이 없을 것이다. 따라서 패딩 옵션에 상관 없이 동일한 결과가 나온다.


0726 추가

Covid-19 예측 과제 에서 직렬 모델을 구성하다가 shape 안 맞는 문제로 몇 시간을 고민했다. 결국 Padding과 Convolution 레이어에서 Padding, Stride의 의미를 뜯어 보았다. 노가다 결과물


이해한 바로는, Convolution 레이어에서나, Pooling 레이어에서나 padding, strides 옵션이 작동하는 원리 자체는 동일하다. 가져가야 할 큰 그림은 다음과 같다.

  1. 옵션 적용 순서 : padding → strides
  2. 연산 전후 사이즈 변화 : \({(N+2P-F)/stride}+1\)

이 내용을 이해하는 데 한해, 머릿속에서 용어를 다음과 같이 정의했다.

  • 연산: Convolution 혹은 Pooling 과정.

  • 입력 : 연산을 적용하기 전의 데이터(주로 이미지).

  • 중간 출력 : Padding 옵션에 따라 입력 데이터를 바꾼 데이터. 아직 연산을 적용하기 전 상태.
  • 출력 : Padding, Strides 옵션 등을 모두 적용해 연산을 적용한 결과 데이터.


Padding 작용 원리

SAME의 경우, 입력과 중간 출력에서 각 변(편의상 이렇게 지칭하지만, 사실은 각 축의 데이터 길이가 될 것이다)의 사이즈가 같아지도록 입력 데이터에 패딩을 붙인다. documentation, 소스 코드를 조금 더 뜯어 봐야 하겠지만, 일단 지금 단계에서 naive하게 이해하기로는, 공식 \({(N+2P-F)}+1\)을 따를 때 중간 출력의 한 변과 입력의 한 변의 사이즈가 같아지도록 P를 찾아 각 변에 패딩을 붙이는 듯하다.

VALID의 경우, 패딩을 붙이지 않는다. 공식에서 P를 0으로 적용하는 것이라 이해했다. 따라서 VALID 옵션이 적용되면, 중간 출력의 한 변의 사이즈가 \({(N-F)}+1\)이 된다.


Stride 작용 원리

위에서 패딩 옵션에 따라 패딩을 적용한 후, 각 변의 사이즈 내에서 커널을 움직일 수 있는 범위 한도 내에서 strides를 적용한다. 이렇게 커널을 움직여 가며 연산을 진행하고, 맞지 않는 사이즈의 data는 drop(혹은 crop)한다.


예시

import numpy as np
import tensorflow as tf
from tensorflow.keras.layers import Conv2D, MaxPooling2D

k_size = 4 # 컨볼루션 커널 사이즈
p_size = 2 # 풀링 커널 사이즈
sample_data = tf.constant(np.arange(1.0, 201.0).reshape(-1, 20, 10, 1), dtype=tf.float32)

위와 같이 샘플 데이터, 컨볼루션 및 풀링 커널 사이즈를 설정하고, 다양한 조합을 실험해 보자. 원래 샘플 데이터의 shape은 (1, 20, 20, 1)이 된다. 데이터 개수와 채널을 나타내는 맨 앞과 뒤의 1은 생략하고, 가운데 이미지 크기를 나타내는 부분만 봐서 그 동작 원리를 이해해 보자.


# conv padding same
sample_conv = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=1, padding='same', activation='linear')(sample_data) # 1) (1, 20, 10, 1)
sample_conv2 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=2, padding='same', activation='linear')(sample_data) # (1, 10, 5, 1)
sample_conv3 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=3, padding='same', activation='linear')(sample_data) # (1, 7, 4, 1)
sample_conv4 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=4, padding='same', activation='linear')(sample_data) # 2) (1, 5, 3, 1)

Convolution에서 padding 옵션이 SAME일 때는 중간 출력 이미지 사이즈가 원본과 동일하게 (20, 10)이다. 이 상태에서,

  • 1) : strides = 1이므로 중간 출력 사이즈와 동일하게 컨볼루션 연산이 적용된다.
  • 2) : strides = 4이므로 중간 출력 사이즈에서 strides가 적용될 수 있는 부분은 인덱스 기준 가로 0, 4, 8, 12, 16, 세로 0, 4, 8이다. 따라서 최종 출력 이미지 사이즈는 (5, 3)이다.


# conv padding same
sample_conv = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=1, padding='valid', activation='linear')(sample_data) # 1) (1, 17, 7, 1)
sample_conv2 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=2, padding='valid', activation='linear')(sample_data) # (1, 9, 4, 1)
sample_conv3 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=3, padding='valid', activation='linear')(sample_data) # 2) (1, 6, 3, 1)
sample_conv4 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=4, padding='valid', activation='linear')(sample_data) # (1, 5, 2, 1)
sample_conv5 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=5, padding='valid', activation='linear')(sample_data) # (1, 4, 2, 1)

Convolution에서 padding 옵션이 SAME이므로 공식에 의해 중간 출력 이미지 사이즈는 17(= 20-4+1) x 7(= 10-4+1) 이 된다. 이 상태에서,

  • 1) : strides = 1이므로 최종 출력 형태는 (17, 7)이다.
  • 2) : strides = 3이므로 strides가 적용될 수 있는 부분은 인덱스 기준 가로 0, 3, 6, 9, 12, 15, 18, 세로 0, 3, 6, 9이다. 따라서 최종 출력 이미지 사이즈는 (6, 3)이다.


# conv padding same + pooling padding same + stride 1 고정
sample_conv = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=1, padding='same', activation='linear')(sample_data) # (1, 10, 4, 1)
sample_pool = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='same')(sample_conv) # (1, 10, 4, 1)
sample_conv2 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=2, padding='same', activation='linear')(sample_data) # (1, 5, 2, 1)
sample_pool2 = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='same')(sample_conv2) # (1, 5, 2, 1)

Convolution 레이어의 출력 shape 계산은 위와 동일한 원리이다. Pooling 레이어는 convolution 레이어의 출력을 입력으로 받는다. pooling 레이어의 padding을 SAME으로 설정했으므로, convolution 레이어의 출력이자 pooling 레이어의 입력 사이즈가 그대로 유지되도록 pooling 레이어의 중간 출력에 패딩이 붙는다. 이 상태에서 strides가 1이므로, 결과적으로 입력과 출력 데이터의 shape이 동일해진다.


# conv padding same + pooling padding same + pooling stride 변화
sample_conv = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=1, padding='same', activation='linear')(sample_data) # (1, 10, 4, 1)
sample_pool = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='same')(sample_conv) # (1, 10, 4, 1) 
sample_conv2 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=2, padding='same', activation='linear')(sample_data) # (1, 5, 2, 1)
sample_pool2 = MaxPooling2D(pool_size=(p_size, p_size), strides=2, padding='same')(sample_conv2) # 1) (1, 3, 1, 1)
sample_conv3 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=3, padding='same', activation='linear')(sample_data) # (1, 4, 2, 1)
sample_pool3 = MaxPooling2D(pool_size=(p_size, p_size), strides=3, padding='same')(sample_conv3) # 2) (1, 2, 1, 1)

strides 옵션이 변화하면, convolution 레이어에서와 마찬가지로 움직일 수 있는 곳까지 pooling 커널이 이동하며 연산이 이루어진다.

  • 1) convolution 레이어의 중간 출력 사이즈인 (5, 2)가 유지되도록 패딩이 붙는다. 그리고 strides가 2이므로 인덱스 기준 가로 0, 2, 4로 이동, 세로 0으로 이동할 수 있다. 따라서 출력 결과 shape은 (3, 1)이 된다.
  • 2) convolution 레이어의 중간 출력 사이즈인 (4, 2)가 유지되도록 패딩이 붙는다. 그리고 strides가 3이므로 인덱스 기준 가로 0, 3으로 이동, 세로 0으로 이동할 수 있다. 따라서 출력 결과 shape은 (3, 1)이 된다.


# conv padding same + pooling padding valid + pooling stride 1 고정
sample_conv = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=1, padding='same', activation='linear')(sample_data) # (1, 10, 4, 1)
sample_pool = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='valid')(sample_conv) # (1, 9, 3, 1)
sample_conv2 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=2, padding='same', activation='linear')(sample_data) # (1, 5, 2, 1)
sample_pool2 = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='valid')(sample_conv2) # (1, 4, 1, 1)
sample_conv3 = Conv2D(filters=1, kernel_size=(k_size, k_size), strides=3, padding='same', activation='linear')(sample_data) # (1, 4, 2, 1)
sample_pool3 = MaxPooling2D(pool_size=(p_size, p_size), strides=1, padding='valid')(sample_conv3) # (1, 3, 1, 1)

convolution 레이어의 출력이 pooling의 입력으로 들어 오고, 중간 출력에서 사이즈가 감소한다. pooling 레이어의 stride는 1이므로, pooling 중간 출력 사이즈가 그대로 유지된다.

태그: ,

카테고리:

업데이트:



hit count image

댓글남기기

참고