[DL] CNN_2.구현
출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo
Tensorflow : 2.2.0
CNN 모델 구현
시계열에 따른 트렌드와 노이즈를 동시에 갖는 Sine 곡선 데이터를 CNN 모델을 활용해 예측한다. 이미지가 아니라 시계열 데이터라는 점에 주목한다.
1. Convolution 1D
개념 강의에서도 살펴 봤듯, 시계열 데이터의 경우 필터가 한 방향으로 이동하기 때문에 1D- Convolution을 적용하는 것이 일반적이다.
입력 데이터의 형태는 LSTM 모델과 마찬가지로 3차원이다.
강사님의 조언
시계열, 문자 등의 데이터에 CNN 모델을 적용할 수 없다는 생각은 하지 말자. 이미지 데이터에서 좋은 성과를 내기는 하지만, 다른 데이터에도 충분히 적용할 수 있다.
한편으로는 입력 데이터의 shape이 3차원인 경우 LSTM, CNN 모델을 사용하기 적합하다. 4차원 이상인 경우에는 CNN 컨볼루션 필터가 이동하는 차원에 맞게 모델을 다르게 선택해주면 된다.
# 모듈 불러오기
import numpy as np
from tensorflow.keras.layers import Inout, Conv1D, Dense, MaxPooling1D, Flatten
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
# data 생성
def createData(X_data, step):
m = np.arange(len(X_data) - step)
x, y = [], []
for i in m:
a = X_data[i : i+step]
b = X_data[i+1 : i+1+step]
x.append(a)
y.append(b[-1]) # 예측해야 할 데이터
X = np.reshape(np.array(x), (len(m), step, 1)) # 입력 데이터 3차원 형태로 만들기
Y = np.reshape(np.array(y), (len(m), 1)) # 라벨 2차원 형태로 만들기
return X, Y
# 시계열 Sine 데이터 생성
n_step = int(input('스텝 설정: '))
n_features = int(input('피쳐 수 설정: ')) # 1
data = np.sin(2*np.pi*0.03*np.arange(1001)) + np.random.random(1001) + np.arange(1001)*0.03 # 노이즈 포함된 Sine 곡선
X_data, y_data = createData(data, n_step)
# Conv1D CNN 모델 구성
X_input = Input(batch_shape=(None, n_step, n_features))
X_conv = Conv1D(filters=30, kernel_size=8, strides=1, padding='valid', activation='relu')(X_input)
X_pool = MaxPooling1D(pool_size=4, strides=1, padding='valid')(X_conv)
X_flat = Flatten()(X_pool)
y_output = Dense(1, activation='linear')(X_flat)
model = Model(X_input, y_output)
model.compile(loss='mse', optimizer=Adam(learning_rate=0.001))
print(model.summary())
# 모델 학습
EPOCHS = int(input('학습 횟수 설정: '))
BATCH = int(input('배치 사이즈 설정: '))
hist = model.fit(X_data, y_data,
epochs = EPOCHS,
batch_size = BATCH)
# loss 시각화
plt.figure(figsize=(8, 4))
plt.plot(hist.history['loss'])
plt.xlabel('Epochs')
plt.ylabel('Train Loss')
plt.title('Loss Function')
plt.show()
# 예측
n_future = int(input('예측할 기간 설정: '))
last_data = np.copy(data[-100:])
X_test = np.copy(last_data) # 예측 데이터
estimates = [X_test[-1]]
for _ in range(n_futures):
x = X_test[-n_step:].reshape(-1, n_step, n_features) # 입력 shape 맞추기
y_pred = model.predict(x)[0][0] # 예측값
estimates.append(y_pred)
X_test = np.insert(X_test, len(X_test), y_pred)
# 예측 시각화
ax1 = np.arange(1, len(last_data)+1)
ax2 = np.arange(len(last_data), len(last_data)+len(estimate))
plt.figure(figsize=(8, 3))
plt.plot(ax1, last_data, markersize=3, color='blue', label='Original Time Series', linewidth=1)
plt.plot(ax2, estimates, markersize=3, color='red', label='Estimated Time Series')
plt.axvline(ax1[-1], linestyle='dashed', linewidth=1)
plt.legend()
plt.show()
다른 부분은 이전 LSTM 모델 구현과 동일하므로, CNN 모델 구성에 주목하자. model.summary()를 통해 확인한 모델 구조는 다음과 같다.
odel: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 20, 1)] 0
_________________________________________________________________
conv1d_1 (Conv1D) (None, 13, 30) 270
_________________________________________________________________
max_pooling1d_1 (MaxPooling1 (None, 10, 30) 0
_________________________________________________________________
flatten (Flatten) (None, 300) 0
_________________________________________________________________
dense (Dense) (None, 1) 301
=================================================================
Total params: 571
Trainable params: 571
Non-trainable params: 0
_________________________________________________________________
None
shape만 잘 맞춰주면 된다. 각 층을 거치면서 shape이 어떻게 변화하는지에도 주목하자. 예컨대, Pooling 레이어에서는 $(13-4+1) * (13-4+1) $ 의 과정을 거쳐 한 변의 길이가 10이 됐다.
MaxPooling1D 레이어를 통과한 뒤, Dense 레이어에 연결되기 전에 텐서를 평활화해주어야 한다. 이후 Dense 층에서는 예측한 값을 그대로 출력해야 하기 때문에, linear 활성화 함수를 사용한다.
결과는 다음과 같다.
| Loss 추이 | 예측 결과 |
|---|---|
 |
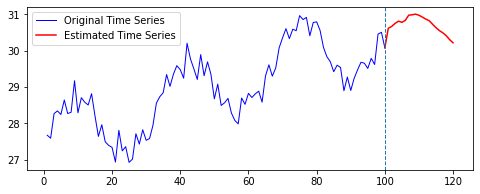 |
2. Convolution 2D
사실 시계열 데이터는 1D-Convolution을 적용해 분석하는 것이 일반적이지만, 연습 차원에서 시계열 데이터를 2차원 데이터로 인식하고 CNN 모델을 구성해 본다. 위에서와 달리, 2개의 Convolution 및 2개의 Pooling 레이어를 구성한다.
# 모듈 불러오기
import numpy as np
from tensorflow.keras.layers import Input, Conv2D, Dense, MaxPooling2D, Flatten
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
# data 생성
def createData(X_data, step, features, channel):
m = np.arange(len(X_data)-step)
np.random.shuffle(m)
x, y = [], []
for i in m:
a = X_data[i : i+step]
b = X_data[i+1 : i+1+step]
x.append(a)
y.append(b[-1])
X = np.reshape(np.array(x), (len(m), step, features, channel)) # 3차원 + channel
Y = np.reshape(np.array(y), (len(m), 1))
return X, Y
# 시계열 Sine 데이터 생성
n_step = int(input('스텝 설정: '))
n_features = int(input('피쳐 수 설정: ')) # 1
n_channel = int(input('채널 축 설정: ')) # 1
data = np.sin(2*np.pi*0.03*np.arange(1001)) + np.random.random(1001) + np.arange(1001)*0.03
X_data, y_data = createData(data, n_step, n_feature, n_channel)
# Conv2D CNN 모델 구성
X_input = Input(batch_shape = (None, n_step, n_feature, n_channel))
X_conv_1 = Conv2D(filters=30, kernel_size=(8, 1), strides=1, padding='same', activation='relu')(X_input)
X_pool_1 = MaxPooling2D(pool_size=(2, 1), strides=1, padding='valid')(X_conv_1)
X_conv_2 = Conv2D(filters=10, kernel_size=(8, 1), strides=1, padding='same', activation='relu')(X_pool_1)
X_pool_2 = MaxPooling2D(pool_size=(2, 1), strides=1, padding='valid')(X_conv_2)
X_flat = Flatten()(X_pool_2)
y_output = Dense(1, output='linear')(X_flat)
model = Model(X_input, X_output)
model.compile(loss='mse', optimizer=Adam(learning_rate=0.001))
print(model.summary())
# 모델 학습
EPOCHS = int(input('학습 횟수 설정: '))
BATCH = int(input('배치 사이즈 설정: '))
hist = model.fit(X_data, y_data,
epochs = EPOCHS,
batch_size = BATCH)
# loss 시각화
plt.figure(figsize=(8, 4))
plt.plot(hist.history['loss'])
plt.xlabel('Epochs')
plt.ylabel('Train Loss')
plt.title('Loss Function')
plt.show()
# 예측
n_future = int(input('예측할 기간 설정: '))
last_data = np.copy(data[-100:])
X_test = np.copy(last_data) # 예측 데이터
estimates = [X_test[-1]]
for _ in range(n_futures):
x = X_test[-n_step:].reshape(-1, n_step, n_features) # 입력 shape 맞추기
y_pred = model.predict(x)[0][0] # 예측값
estimates.append(y_pred)
X_test = np.insert(X_test, len(X_test), y_pred)
# 예측 시각화
ax1 = np.arange(1, len(last_data)+1)
ax2 = np.arange(len(last_data), len(last_data)+len(estimate))
plt.figure(figsize=(8, 3))
plt.plot(ax1, last_data, markersize=3, color='blue', label='Original Time Series', linewidth=1)
plt.plot(ax2, estimates, markersize=3, color='red', label='Estimated Time Series')
plt.axvline(ax1[-1], linestyle='dashed', linewidth=1)
plt.legend()
plt.show()
일단 시계열 데이터에 channel 축을 추가한다. 원래 이미지라면 어떤 색 공간에 위치해 있는가에 따라 달라지겠지만, 시계열 데이터이므로 channel을 1로 설정한다.
이제 필터가 2개의 방향으로 움직이기 때문에 가로로 몇 칸 움직일지, 세로로 몇 칸 움직일지를 생각해 kernel_size에 지정한다. 이전에 이미지로 CNN 모델 구성했을 때와 동일한 원리이다. Pooling 레이어에서도 pool_size를 2차원으로 지정한다.
모델 전체 구조는 다음과 같다.
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 20, 1, 1)] 0
_________________________________________________________________
conv2d (Conv2D) (None, 20, 1, 30) 270
_________________________________________________________________
max_pooling2d (MaxPooling2D) (None, 19, 1, 30) 0
_________________________________________________________________
conv2d_1 (Conv2D) (None, 19, 1, 10) 2410
_________________________________________________________________
max_pooling2d_1 (MaxPooling2 (None, 18, 1, 10) 0
_________________________________________________________________
flatten (Flatten) (None, 180) 0
_________________________________________________________________
dense (Dense) (None, 1) 181
=================================================================
Total params: 2,861
Trainable params: 2,861
Non-trainable params: 0
_________________________________________________________________
None
결과는 다음과 같다.
| Loss 추이 | 예측 결과 |
|---|---|
 |
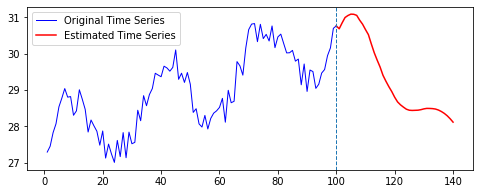 |


댓글남기기