[DL] DARNN_1. 논문 리뷰

^{논문( 출처 ): A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction} 

A Dual-Stage Attention-Based Recurrent Neural Network for Time Series Prediction

시계열 데이터 예측에 두 단계의 attention을 적용한 논문이다. 해당 논문에서 적용한 Dual-Stage Attention의 개념이 무엇인지 알아보자.

1. Introduction

시계열 예측을 수행하기 위해 많은 연구가 이루어져 왔다. 그 중에서도 예측하고자 하는 변수(이하 target series)와 외생 변수(이하 driving series)들을 함께 사용하여 비선형 mapping function을 학습하고자 하는 NARX(Nonlinear Autoregressive Exogenous) 모델에서는 attention 기법을 사용한 RNN 기반의 인코더-디코더 네트워크가 SOTA라고 알려져 있다.

Typically, given the previous values of the target series, \(i.e. (y_1, y_2, …, y_{t-1})\) with \(y_{t-1} \in \mathbb{R}\), as well as the current and past values of \(n\) driving (exogenous) series, \(i.e. (\mathbf{x}_1, \mathbf{x}_2, …, \mathbf{x}_t)\) with \(\mathbf{x}_t \in \mathbb{R^{n}}\), the NARX model aims to learn a nonlinear mapping to the current value of target series \(y_t\), \(i.e. \ \hat{y_{t}} = F(y_1, y_2, …, y_{t-1}, \mathbf{x}_1, \mathbf{x}_2, …, \mathbf{x}_t)\), where \(F(\cdot)\) is the mapping function to learn.

(…)

Therefore, it is natural to consider state-of-the-art RNN methods, \(e.g.,\) encoder-decoder networkss[Cho \(et \ al.\), 2014b; Sutskever \(et \ al.\), 2014] and attention based encoder-decoder networks [Bahdanau \(et \ al.\), 2014], for time series prediction.

그러나 해당 논문은 시계열 예측에 있어 위의 SOTA NARX 모델이 다음과 같은 문제를 갖는다고 지적한다.

첫째, RNN 기반의 인코더-디코더 네트워크는 input sequence가 길어질수록 모델의 성능이 하락한다는 문제가 있다. 특히 target series와 driving series의 길이가 상대적으로 긴 시계열 예측에서는 이 문제가 더 부각될 수 있다. 둘째, 시계열 예측에 있어 복수의 driving series 변수들 중 target series를 예측하는 데 있어 중요한 driving series 변수가 무엇인지 파악할 수 없다.

위와 같은 문제를 해결하기 위해 이 논문은 DA-RNN(dual-stage attention-based recurrent neural network)이라는 두 단계의 attention 메커니즘을 제안한다. 이 attention 메커니즘을 RNN 기반 인코더-디코더 네트워크에 적용함으로써, 시계열 예측 분야에 있어 더 나은 성능을 얻을 수 있다는 것이다.

2. Dual-Stage Attention-Based RNN

논문에 소개된 모델의 전체 개요는 다음과 같다.

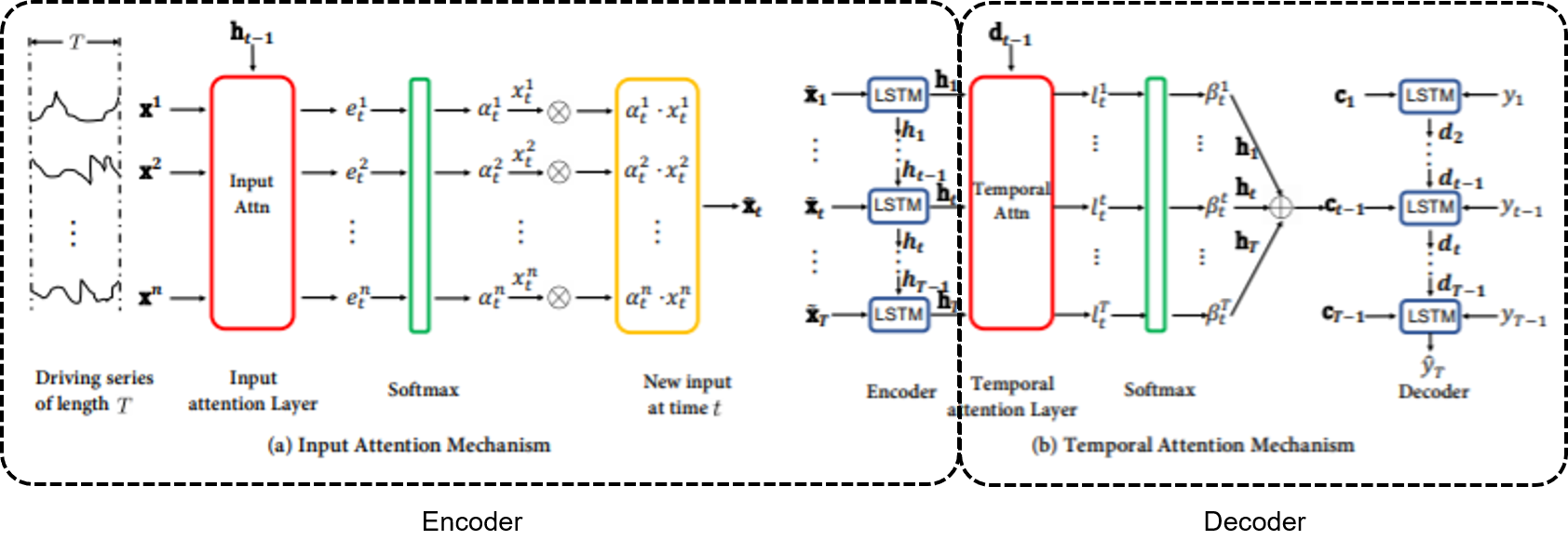
• 순환신경망(논문에서는 LSTM을 사용했다) 네트워크 기반의 인코더-디코더 네트워크이다.
• 인코더는 이전 인코더의 은닉 상태를 참고하여 각 시점(timestep)에서 target series와 연관이 가장 큰 driving series를 파악하는 attention 스코어를 계산(그림 a)한다.
• 디코더는 이전 디코더의 은닉 상태를 참고하여, 전체 시점 중 target series와 연관이 가장 큰 인코더 은닉 상태가 무엇인지 파악하는 attention 스코어를 계산(그림 b)한다.

인코더에서 relevant driving series를 선택하기 위해 이루어지는 attention 메커니즘을 Input Attention, 디코더에서 relevant encoder hidden state를 선택하기 위해 이루어지는 attention 메커니즘을 Temporal Attention 메커니즘이라 한다.

참고 : 인간의 attention 메커니즘

논문에서는 위와 같이 두 단계로 이루어지는 attention 메커니즘이 인간의 그것을 닮은 novel(이라는 단어를 참 좋아하는 듯하다) 메커니즘이라고 한다.

Some theories of human attention [Hubner \(et \ al.\), 2010] argue that behavioral results are best modeled by a two-stage attention mechanism. The first stage selects the elementary stimulus features while the second stage uses categorical information to decode the stimulus. Inspired by these theories, we propose a novel dual-stage attention-based recurrent neural network for time series prediction. In the encoder, we introduce a novel input attention mechanism that can adaptively select the relevant driving series. In the decoder, a temporal attention mechanism is used to automatically select relevant encoder hidden states across all time steps.

논문에서는 실험을 위해 SML 2010 dataset과 NASDAQ 100 Stock dataset을 사용했는데, 그 중 후자를 사용한 실험이 앞으로 내가 진행하고자 하는 연구와 비슷하다. 따라서 해당 데이터(출처: cseweb.edu)를 사용해 모델 아키텍쳐를 톺아 보기로 했다.

2.1. Notation and Problem Statement

예측하고자 하는 target series는 NASDAQ 100 index(NDX)이고, 해당 지수를 예측하기 위해 사용할 driving series는 NASDAQ 100 index에 편입되어 있는 104개 회사들의 주가이다. 이 데이터를 이용해 논문에서의 notation을 다음과 같이 나타낼 수 있다.

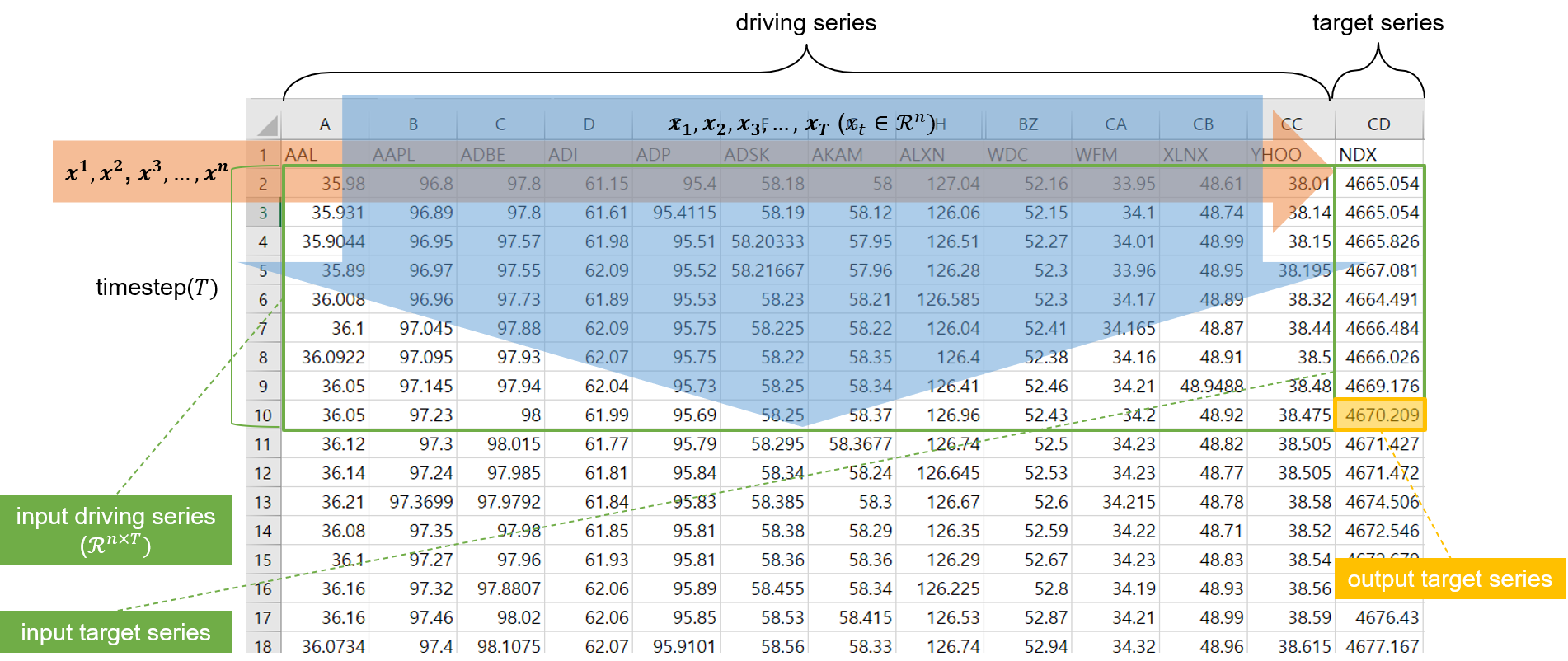
• input data: \(T\) timestep 동안의 \(n\)개의 driving series와 \(n-1\)개의 target series로 이루어진 텐서.
  • 위 첨자: driving series의 순서.
  • 아래 첨자: timestep의 순서.
• output data: \(T\) timestep에서의 target series.

이 때, 논문에서의 시계열 예측 모델이 학습해야 할 mapping function \(F\)는 다음과 같다.

\(\\ \\ \hat{y_T} = F(y_1, y_2, ..., y_{T-1}, \mathbf{x}_1, \mathbf{x}_2, …, \mathbf{x}_t)\)

즉, 이 모델이 해결해야 할 문제는, 1) $n$개의 driving series와 2) $n-1$개의 target series가 주어졌을 때, 3) 그 다음 step에서의 target series가 무엇이 될지 예측하는 회귀 문제이다. 이 문제를 풀기 위해 해당 모델은 두 단계의 attention 메커니즘을 적용할 것이며, 회귀 문제를 풀어야 하기 때문에 loss function으로 MSE loss를 사용한다.

2.2. Model

Encoder

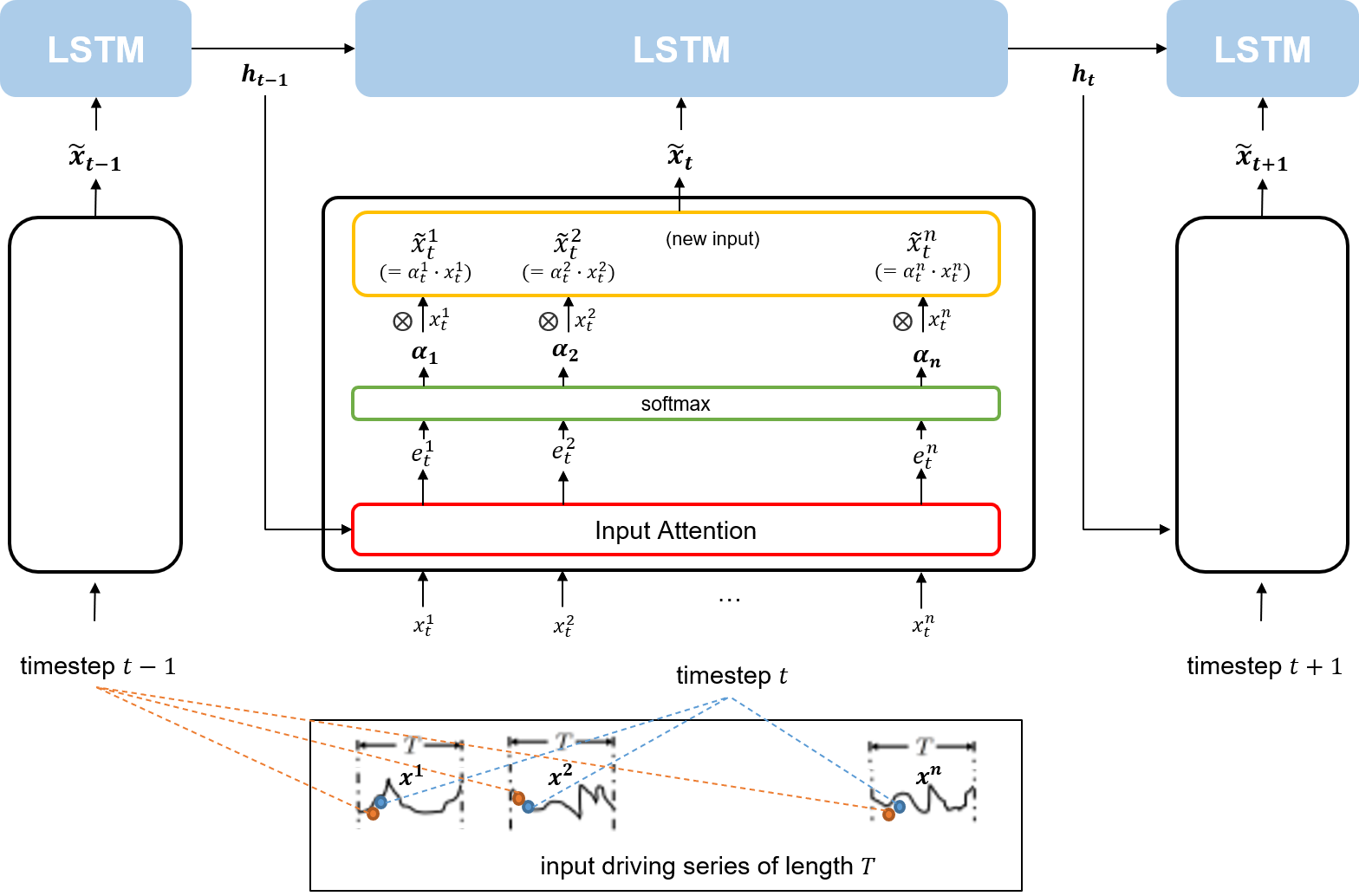
인코더에는 $T$만큼의 timestep 길이를 갖는 $n$개의 driving series가 input으로 들어간다. 이후 인코더는 각 timestep에서 $n$개의 driving series를 대상으로 Input Attention 메커니즘을 적용한 새로운 input vector(\(\tilde{x}_t\))를 만들어 LSTM 셀에 주입한다. 이 때, 만들어진 새로운 input vector는 이전 인코더의 LSTM 셀에서의 hidden state를 참고해 attention weight을 적용한 것이다. 즉, 직전 timestep에서의 hidden state와 연관성이 얼마나 높은지가 새로운 input vector에 적용되어 있는 것이다.

Decoder

^{원 논문에서는 인코더와 디코더에서의 attention weight 계산 과정을 다르게 보여주기 위해 다른 notation을 사용했다.}

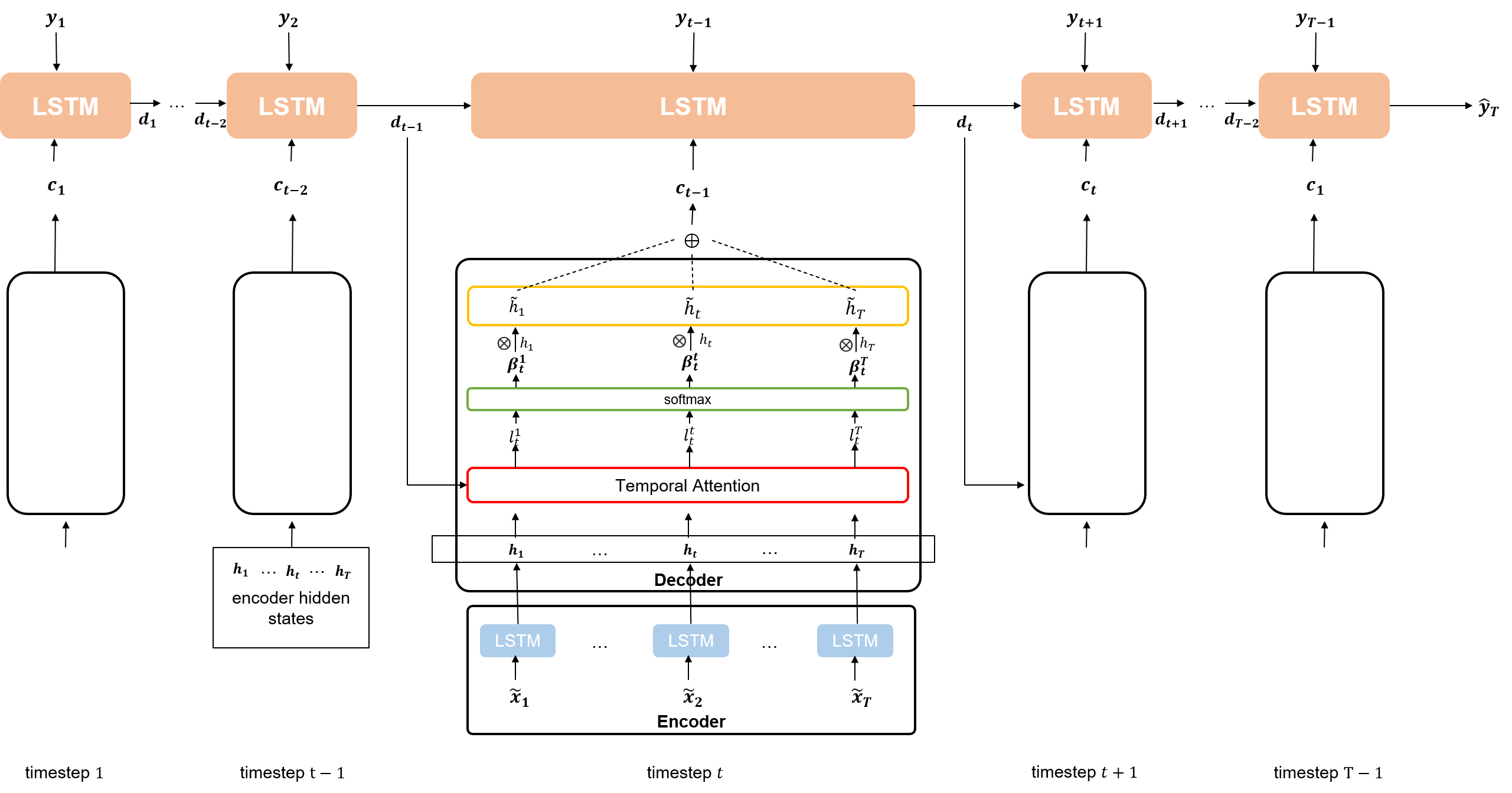
디코더는 인코더의 LSTM에서 나오는 각각의 hidden state($h_i, where \ i \in {1, 2, …, T}$)에 대해 Temporal Attention 메커니즘을 적용한 새로운 context vector($c_1, c_2, …, c_{T-1}$)를 만든다. 그리고 주어진 $T-1$개의 target series와 context vector를 concat하여 LSTM 셀에 주입한다. 이 때, 만들어진 새로운 context vector는 이전 디코더의 LSTM 셀을 참고해 \(T\)개의 인코더 hidden state 중 어떤 것이 가장 연관성이 높은지를 계산한 attention weight을 적용한 것이다. 즉, 직전 timestep에서의 디코더 hidden state와 얼마나 연관성이 높은지가 context vector에 적용되어 있는 것이다.

결과적으로 이렇게 디코더에서 context vector와 previous target series를 concat해 LSTM 셀에 주입함으로써 $T$ 시점에서의 target series를 예측할 수 있게 된다.

3. Experiments

결과적으로는 시계열 예측에서 Dual-Stage Attention 모델을 사용하였을 때 아래와 같이 더 좋은 결과를 거두었다고 한다.

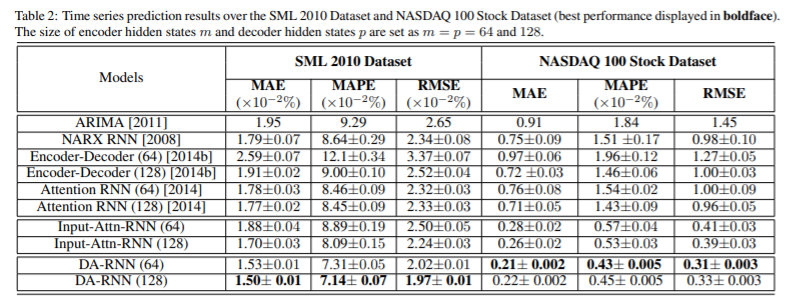
4. 결론

시계열 예측 모형을 개발할 때 참고하기 좋은 논문이라고 보여 리뷰했다. attention 메커니즘이 두 번 적용되는 만큼 구현 시에는 Tensor shape을 잘 보아야 할 것이라 생각된다. 지수 예측 연구를 진행하며, 예측하고자 하는 지수에 어떠한 driving series가 영향을 미치는지 시각화할 수 있는 방법도 고민해볼 필요가 있다.