[AI] Training Deep AutoEncoders for Collaborative Filtering 리뷰

^{논문( 출처 ) Training Deep AutoEncoders for Collaborative Filtering. 출처가 명시되지 않은 모든 자료(이미지 등)는 원 논문의 것입니다.}

NVIDIA에서 Netflix Prize의 rating prediction 문제를 풀기 위해 deep한 오토인코더 네트워크를 구성한 후 발표한 논문이다. 6개의 층으로 이루어진 깊은 네트워크를 구성함으로써 rating 예측 성능을 높였는데, 깊은 네트워크를 사전학습 없이 구현하기 위해 다양한 딥러닝 기술과 새로운 학습 알고리즘(dense re-feeding)을 도입한 것이 성공 요인이었다.

깊은 오토인코더 네트워크를 어떻게 구현했는지가 핵심이기 때문에, 추천시스템 전반 및 딥러닝을 추천시스템에 적용한 선행 연구를 다룬 Introduction 파트는 생략하고 모델에 대한 파트부터 리뷰하도록 한다.

Model

오토인코더 는 입력 데이터 \(x\)와 인코더와 디코더를 통과하여 나온 \(encoder(decoder(x))\)의 차이가 최소가 되도록 학습하는 네트워크이다. 주로 차원 축소의 목적으로 이용하는데, 인코더의 coding layer를 통과하여 나온 입력 데이터의 축소된 벡터를 얻으려 한다.

추천시스템에서는 협업 필터링의 rating prediction 태스크를 수행하기 위한 목적으로 오토인코더 네트워크를 사용한다. 즉, sparse한 사용자 벡터(\(\in \mathbb{R}^n\) ^{: $n$은 아이템의 개수})를 입력으로 받아 $f(x)$를 출력하는데, 이 $f(x)$는 dense한 벡터로 사용자의 모든 아이템에 대한 rating 예측을 갖고 있다.

Loss Function

오토인코더 네트워크가 유저 벡터에서 이미 0인 rating을 예측하는 것은 적절하지 않으므로, U-Autorec 관련 연구에서 제안한 MMSE를 손실함수로 사용한다.

\[MMSE = \frac {m_i * (r_i - y_i)^2} {\Sigma_{i=0}^{i=n} m_i}\]

• \(r_i\) : 사용자의 \(i\)번째 아이템에 대한 실제 rating
• \(y_i\) : 사용자의 \(i\)번째 아이템에 대한 예측 rating
• \(m_i\) : masking으로, \(r_i\)가 0일 때 0이고, 그렇지 않을 때 1

이 때, \(RMSE = \sqrt {MMSE}\) 의 관계가 있다. (결론적으로 \(RMSE\)를 최소화하기 위해 \(MMSE\)를 최소화해도 된다는 의미인 듯하다.)

학습 알고리즘

해당 논문은 dense re-feeding이라는 새로운 학습 알고리즘을 사용한다. 기존의 forward pass, backward propagation이 한 번씩 이루어지던 과정을 re-feeding을 통해 여러 번 수행하도록 함으로써 예측 성능을 높였다.

아이디어는 다음과 같다. sparse한 입력을 받아 dense한 출력을 내는 오토인코더가 만약 완벽한 예측을 수행한다고 가정해 보자. 그렇다면 오토인코더가 sparse한 사용자 벡터 \(x\)를 입력으로 받아 출력으로 낸 새로운 사용자 벡터 \(f(x)\)는, 사용자가 기존에 평가를 하지 않았던 아이템에 대해 평가를 한 뒤 만들어지는 새로운 사용자 벡터와 같아야 한다. 즉, 이러한 이상적인 시나리오가 성립한다면, \(f(x)\)와 \(f(f(x))\)가 같아야 한다. (=논문에서는 이를 \(y=f(x)\)가 fixed point여야 한다고 기술한다)

이러한 제한을 적용하여 훈련 업데이트를 수행하기 위해서, 각 이터레이션마다 dense re-feeding step(= step 3, 4)를 추가한다.

• step 1: sparse한 사용자 벡터 \(x\)를 입력으로 받아 dense한 사용자 벡터 \(f(x)\) 및 \(MMSE\) loss를 계산 → forward pass 1
• step 2: 그래디언트 계산 후 가중치 업데이트 → backward pass 1
• step 3: 계산된 \(f(x)\)를 다시 입력으로 \(f(f(x))\)를 및 \(MMSE\) 계산 (이 단계에서 \(f(x)\)와 \(f(f(x))\)는 모두 dense한 상태이고, 이를 다시 네트워크에 주입하기 때문에 dense re-feeding이라고 명명한 듯?!) → forward pass 2
• step 4: 그래디언트 계산 후 가중치 업데이트 → backward pass 2

해당 논문에서는 step 3과 step 4를 한 번씩만 넣었는데, 더 넣어도 된다 (computing power 등 여력이 되어야 가능한 일이 아닐까..)

Experiment and Results

유명한 Netflix Prize 문제로, past rating을 이용해 missing rating을 예측하는 문제이고, 평가 지표는 \(RMSE\)다.

Experiment Setup

train, test set 구성은 논문의 표로 대체한다.

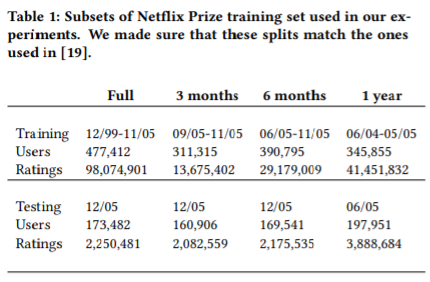
그 외에 실험 초기 조건으로 batch size는 128, momentum 0.9의 SGD, Xavier 초기화를 사용하였다.

Activation Type

어떤 활성화 함수를 사용해야 하는지 판단하기 위해, 다음의 활성화 함수들을 사용했다. 이 때, 테스트 환경은 4개의 은닉층을 가진 오토인코더 네트워크였으며, 각각의 층에서 은닉 노드는 128개였다.

• SIGMOID
• RELU(Rectified Linear Units)
• RELU6(\(max(ReLU(x), 6)\))
• TANH(Hyperbolic Tangent)
• ELU(Exponential Linear Units)
• LRELU(Leaky RELU)
• SELU(Scaled Exponential Linear Units)

실험 환경을 동일하게 설정했으나, rating scale이 1~5이기 때문에, TANH, SIGMOID를 사용한 모델에서는 디코더의 마지막 레이어 활성 함수를 linear로 사용했다. 이외에 다른 모델에서는 모든 레이어마다 동일한 활성화 함수를 적용한다.

아래의 실험 결과를 통해 ELU, SELU, LRELU가 다른 것들에 비해 좋은 성능을 냄을 확인할 수 있다.

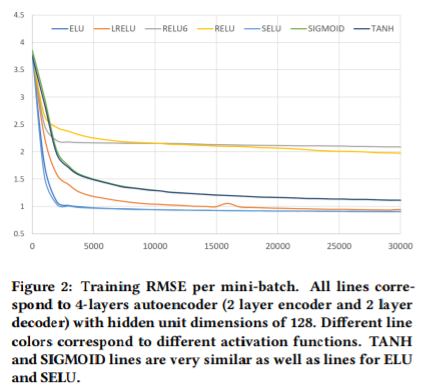
좋은 성능을 내는 활성화 함수의 경우 다음의 특징을 가지고 있었다.

• non-zero negative part
• unbounded positive part

따라서 위의 특성들이 각 레이어의 활성화 함수로 사용될 때 성공적인 학습이 이루어질 수 있다고 판단했고, 논문의 저자들은 SELU 기반 네트워크를 사용한다.

Over-fitting the Data

실험에서 사용할 수 있는 가장 큰 데이터인 Netflix Full 데이터의 경우도, 현대 딥러닝 알고리즘과 하드웨어 환경에서는 small task이다. 따라서 인코더와 디코더의 계층을 1개로 구성할 경우, 은닉 노드 수가 512만 되더라도 과적합이 일어난다. 아래 결과가 이를 증명한다.

^{하나의 레이어 내 은닉 노드 수가 512에서부터 넓어지기만 하더라도 과적합이 일어난다.}

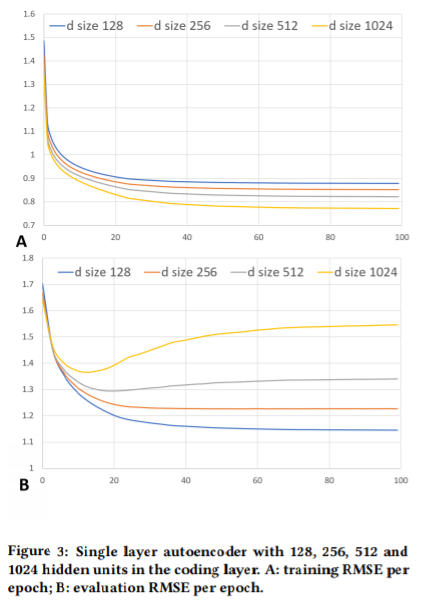
Going Deeper

따라서 더 많은 레이어를 추가해 네트워크를 일반화한다. 과적합을 피하기 위해 각 계층의 은닉 노드 수는 128로 제한(=계층을 넓게 만들어도 훈련 손실은 감소하지만, 위에서 본 것처럼 과적합이 일어날 수 있다)하고, 레이어만 추가함으로써 일반화 성능이 향상되는지 관찰했다.

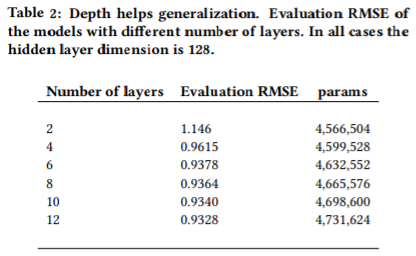
실제로 레이어를 추가할수록 성능이 향상됨을 확인할 수 있다. 다만, 인코더와 디코더 각각을 구성하는 레이어가 4개 이상이 될 경우에는, 표면적으로 봉는 \(RMSE\) 값은 증가하지만, 실제로 반환되는 값이 감소한다.

참고 : diminishing returns의 의미

원문에서는 위의 경우에 대해 ‘After that, blindly adding more layers does help, however it provides diminishing returns.’라고 기술해 놓았다. 처음 팀원과 논의했을 때에는 학습 파라미터 수가 증가함에 비해 \(RMSE\) 성능이 크게 향상되는 것은 아니라고 이해했는데, 포스팅 정리하다 보니 말 그대로 return으로 돌아 오는 rating 값이 감소한다는 의미일 수도 있을 것 같다는 생각이 든다. 어쨌든 맹목적으로 레이어를 늘린다고 계속해서 성능이 좋아지는 것은 아니고, 적정선이 있다는 정도로만 이해하고 넘어간다.

실제 인코더와 디코더를 구성하는 각 레이어가 1개이고, 해당 레이어의 은닉 노드가 256개일 경우는 위의 표에 등장한 것보다 훨씬 많은 9,115,240개의 학습 파라미터를 갖는데, 그럼에도 불구하고 위의 모델들보다 \(RMSE\)가 훨씬 높다고 한다. 이를 통해 레이어를 추가하는 것이 좋다는 것을 알 수 있다.

Dropout

논문의 저자들은 위와 같은 작업을 다양한 하이퍼 파라미터(각 레이어의 은닉 노드 수, 레이어 수 등)에 대해 반복함으로써 모델 아키텍쳐가 \(n, 512, 512, 1024, 512, 512, n\)일 때 가장 좋다는 것을 발견했다. 이 모델에서는 인코더가 3계층을 가지며, 마지막 coding layer가 1024개의 은닉 노드를 갖는다.

해당 모델은 빠르게 과적합되기 때문에, 이를 해결하기 위한 정규화 기술로 dropout을 적용했다. 여러 dropout 비율 중, 높은 편인 0.8이 제일 좋은 성능을 보였다. dropout 비율에 따른 성능은 다음과 같다.

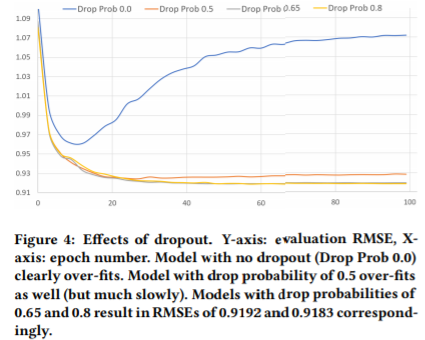
그러나 모든 레이어에 dropout을 적용한다고 성능이 개선되는 것은 아니었다. 인코더의 출력(=마지막 coding 레이어를 통과하여 나온 결과)에만 dropout을 적용할 때 일반화 성능이 좋아졌다.

Dense re-feeding

2.5.까지의 결과에서 찾아낸 최적의 모델 구조는 6개의 레이어로 이루어진 \(n, 512, 512, 1024, dp(0.8), 512, 512, n\)이다. 이러한 모델 구조에 dense re-feeding 학습 알고리즘을 적용했다.

결과적으로, dense re-feeding만을 적용하는 것으로는 성능이 향상되지 않았다. 그러나 높은 학습률(0.5)과 함께 dense re-feeding 학습 알고리즘을 사용하면, 성능이 향상되었다. 그러나 dense re-feeding 학습 알고리즘을 적용하지 않고 높은 학습률을 적용하면, 성능은 향상되지 않는다.

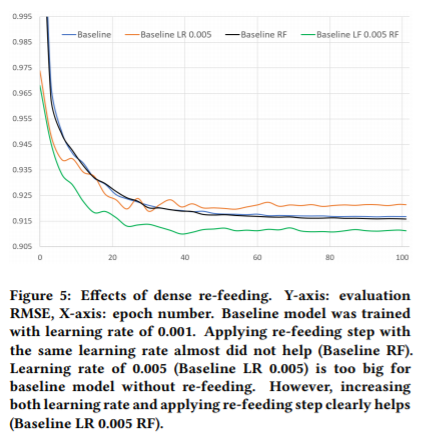
Comparison with other methods

논문의 저자들은 자신들이 찾아낸 best model을 다른 모델들과 비교한다. 다만, 이들의 모델은 temporal dynamics를 고려하지는 않았다. 그럼에도 불구하고 다른 모델보다 더 좋은 성능을 냈다.

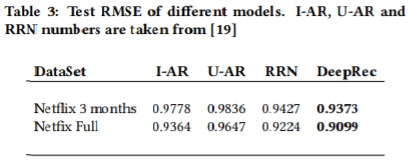
그러나 데이터의 양이 더 적은 Netflix 3 months의 경우, 과적합이 발생했다. 따라서 해당 데이터를 사용하는 경우 모델의 복잡도를 감소시켜야 했다.

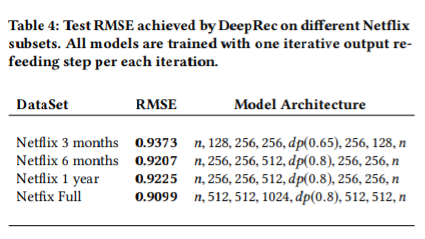
Conclusion

결론적으로 해당 논문은 굉장히 깊은 오토인코더가 적절한 딥러닝 기술 및 (논문이 제안하는) dense re-feeding 학습 알고리즘을 활용한다면, 적은 데이터에도 불구하고 잘 학습되고, 추천시스템의 rating prediction 태스크에서 좋은 성능을 나타낼 수 있음을 보여준다.

결론

GPU의 대명사 NVIDIA답게, deep한 네트워크를 구성하기 위한 기술의 끝판왕을 다룬 느낌이다. 다른 논문들과 달리 novel한 네트워크 아키텍쳐를 제시하기보다는, 네트워크를 어떻게 더 깊이 만들 수 있을지에 집중했다는 점이 신선했다.

더 알아보고 싶거나 궁금했던 점은 다음과 같다.

• context-based는 content-based 추천시스템일까? 도대체 왜 논문마다 추천시스템을 소개하는 부분이 다른 건지..

• 오토인코더는 왜 PCA의 strict generalization인지?
• 좋은 성능을 보인 활성화 함수들은 왜 그랬을까? 특히 이 데이터에 대해 그렇게 좋은 성능이 나타날 수 있는 이유가 있었을까?
• 이 논문은 temporal dynamics를 고려하지 않았는데, 좋은 성적을 거둔 팀의 논문 에서는 그것을 고려하는 것이 중요하다고 했다.
  • temporal dynamics를 고려하는 모델은 무엇인가? 굳이 딥러닝 기반이 아니더라도. 예컨대, TimeSVD++.
  • 해당 논문의 네트워크를 구현한 공개된 코드에서 temporal dynamics를 추가하려면 어떻게 해야 할지?