[DL] GAN_1.개념

^{출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다.}

GAN 이해하기

1. 개요

GAN 모델은 우리 말로 생성적 적대 신경망이라고 번역되는 모델로서, 그 약자를 풀어 쓰면 Generative Adversarial Networks가 된다. 어느 것이든 이름이 중요하지 않은 것은 없겠지만서도, 이 모델은 이름에 모델의 모든 아이디어가 담겨 있다는 점에서 특히 더 이름을 유심히 살펴 봐야 한다고 생각한다.

첫째, Generative는 GAN이 생성 모델이라는 것을 의미한다. 이전에 잠시 개념만 살펴보았던 VAE 나 RBM 과 같이, 데이터를 생성해 낸다.

그렇다면 컴퓨터가 pluasible한 데이터를 생성해 내기 위해 중요한 것은 무엇일까. 수학적으로 학습하는 컴퓨터의 입장에서는 실제 데이터의 분포를 알아 내고, 그와 비슷한 분포로부터 데이터를 만들어 내고자 할 것이다. 따라서 생성 모델은 실제 데이터와 가장 비슷한 분포를 찾아 내고자 한다.

질문: VAE vs. GAN?

VAE와 GAN의 경우, 목적 자체 측면에서 보자면 데이터 생성으로 비슷하다. 그러나 기술적으로는 무관하다. VAE의 경우 가우지안 분포 등 확률 분포를 가정해야 하지만, GAN은 분포에 대한 가정 없이도 비지도학습만으로 데이터를 생성해낼 수 있다.

둘째, Adversarial은 GAN의 학습 방식이 적대적이라는 것을 의미한다. 적대적이라 함이 잘 와닿지 않을 수 있으므로, 원래 논문의 표현을 살펴 봄으로써 그 의미를 이해해 보자.

In the proposed adversarial nets framework, the generative model is pitted against an adversary: a discriminative model that learns to determine whether a sample is from the model distribution or the data distribution.

The generative model can be thought of as analogous to a team of counterfeiters, trying to produce fake currency and use it without detection, while the discriminative model is analogous to the police, trying to detect the counterfeit currency. Competition in this game drives both teams to improve their methods until the counterfeits are indistiguishable from the genuine articles.

다시 말해, GAN에는 Generative Model과 Discriminative Model의 두 가지 모델이 있다. 두 모델은 서로 경쟁하며 발전해 나간다. 각각의 모델을 위조지폐범과 경찰에 비유한 것이 인상적이다. 위조지폐범인 Generative Model은 위조 지폐에 비유할 수 있는 가짜 지폐를 만들어 내고, 경찰인 Discriminative Model은 위조 지폐 구분 기술을 발전시킨다. 그리고 결과적으로는 위조지폐범의 위폐 제조 기술이 계속 발전하여 indistinguishable해질 때까지 두 모델 간 경쟁이 계속 된다.

셋째, Networks는 GAN 모델이 인공신경망 네트워크를 기반으로 하고 있음을 의미한다. 즉, GAN은 데이터를 생성하기 위한 인공신경망 네트워크로서, 학습한 데이터를 모방하여 새로운 데이터를 생성하는 기능을 하는 모델이다. 이제 GAN 모델이 작동할 수 있게 하는 네트워크의 구조와 손실 함수에 대해 알아보자.

2. 구조

^{GAN 모델 구조를 간단히 나타내면 다음과 같다. 위의 모든 네트워크를 총칭해 GAN이라 한다.}

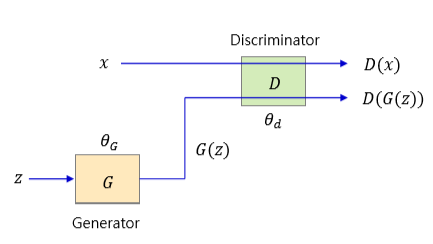
본격적인 네트워크 구조를 살피기에 앞서, 용어에 익숙해지자. 이후 코드 구현 단계에서 동일한 용어를 계속해서 사용하게 될 것이다.

가장 중요한 것으로, 두 가지 모델이 있다.

• discriminator : 실제 데이터, 가짜 데이터를 판별하는 모델.
• generator : 임의의 랜덤 데이터를 받아 들여 진짜 같은 가짜 데이터를 생성하는 모델.

이제 discriminator를 D, generator를 G라 칭한다. 두 모델에 입력되는 데이터로 다음의 두 가지 종류가 있다.

• x : 실제 데이터
• z : 랜덤 데이터

그 중에서도 G가 z를 입력으로 받아 새로이 생성해 낸 데이터를 G(z)라고 한다. 당연히 G(z)의 분포는 x의 분포를 닮아 있을 것이다.

D는 감별사이므로, 실제 데이터가 들어 오면 1, 가짜 데이터가 들어 오면 0을 출력한다. G는 위조 데이터를 만들어 내야 하므로, D가 가짜 데이터가 들어올 때에도 1을 출력하도록 방해한다.

모델의 학습이라는 것은 곧 파라미터를 업데이트하는 것을 의미한다. 위 그림을 다시 보며 학습이 어떻게 이루어지는지 살펴 보자. 실제 데이터 X와 랜덤 데이터 z로부터 G를 거쳐 생성된 G(z)가 D에 입력된다. 그리고 D는 D(x)는 1, D(g(z))는 0이 되도록 자신의 가중치와 bias인 𝜃𝑑를 업데이트한다. 반면, G는 D(g(z))는 1(혹은 그에 가까운 값)이 나오도록 𝜃𝐺를 업데이트한다.

여기서 경제학의 내쉬 균형 개념이 등장한다. (반가워라) GAN 네트워크에서 학습이 완료되는 것은 곧 두 모델이 경쟁을 마치고 내쉬 균형에 도달했음을 의미한다.

GAN 네트워크는 두 모델이 각자 최선의 목적을 달성할 수 있도록 학습시킨다. 결과적으로, 이 싸움에서 내쉬 균형은 G가 최종 승자가 되는 상태이다. 모든 학습이 완료된 후, G는 정말로 진짜를 닮은 가짜 데이터를 생성하게 되며, D는 정말로 진짜와 가짜를 구별하지 못한다. 따라서 내쉬균형 상태에서 D는 어떠한 데이터를 입력 받더라도 0.5 근처의 값을 출력하게 된다.

3. 학습 알고리즘

상술하기를, GAN 네트워크가 D, G 모두가 최선의 목적을 달성할 수 있도록 한다고 했다. 이 말은, GAN 네트워크에서의 학습이 다른 신경망과 달리 한 가지의 최적화(min or max)만을 위한 것이 아님을 드러낸다.

두 모델 간 경쟁을 구현하기 위해 GAN 모델은 다음과 같은 loss function을 사용한다.

\[\min_{G}\max_{D} V(D, G) = E_{x \tilde \ P_{Data}(x)}[logD(x)] + E_{z \tilde \ P_{z}(z)}[1-logD(G(z)]\]

D, G 각자는 V(D, G)라는 목적함수를 가지고 min-max 게임을 한다.

^{아래 원리를 이해하기 위해 꼭 로그 함수의 그래프를 머릿속에 그려 놓자! (출처: 위키피디아)}

먼저 Discriminator의 학습을 보자. D는 V(D, G)를 최대화하도록 학습한다. 따라서,

• D(x)가 1일 때: 진짜 데이터를 진짜라고 판별하고,
• D(G(z))가 0일 때: 가짜 데이터를 가짜라고 판별해야,

자신의 목적을 달성할 수 있다.

다음으로 Generator의 행동 원리를 보자. G는 V(D, G)를 최소화하도록 학습한다. 따라서,

• D(x)는 무관하고: D가 진짜 데이터를 진짜라고 판단하는 것에 개의치 않고,
• D(G(z))가 1일 때: D가 가짜 데이터를 진짜라고 판별해야,

자신의 목적을 달성할 수 있다.

학습이 완료된 후 D는 0.5를 최적의 출력으로 내놓게 된다. 수학적 증명은 논문과 강사님의 자료를 참고하자. 다만 다음의 두 가지를 기억하면 된다.

첫째, 최적의 D 출력값이 나오는 경우이다. G를 고정시킨 상태에서 D를 학습시켰을 때 D의 출력값은 다음과 같다.

\[D^*_G{(x)} = \frac {P_{data}(x)} {P_{data}(x) + P_g(x)}\]

직관적으로 이해했을 때, 위에서 0.5가 나오기 위해서는 실제 데이터의 분포인 Pdata와 G가 만들어 낸 가짜 데이터의 분포인 Pg가 일치해야 한다. 결론적으로,

• G는 실제 데이터 분포를 모방한 가짜 분포를 생성하는 데에 성공했으며,
• D는 실제 데이터와 가짜 데이터의 분포를 구분해 내지 못하고, 0.5만을 출력한다.

둘째, G의 학습을 통해 진짜 데이터와 가짜 데이터의 분포가 유사해져 갈 때, 위의 loss 함수가 수렴해 가는 값이다. 증명을 거쳐 유도된(…) 식에서 결론적으로 위 식의 Global minimum은 값은 -log4, 약 -1.3863 정도에 수렴해 가게 된다.

논문에 소개된 pseudo code를 보면서 GAN 네트워크의 학습이 어떻게 이루어지는지 이해해 보자.

첫째, D의 경우, V(D, G)를 Maximize하기 위해 손실 함수의 그래디언트를 ascending시키는 방향으로 학습이 이루어진다. 그러나 실제 코드로 구현할 때는 편의상 loss function에 -를 붙여 minimize하는 방향으로 학습한다.

참고

실제로 이후 Tensorflow로 low-level GAN 코드를 구현할 것이다. 이 때 D의 loss 함수에 -를 붙이게 되는데, 그러면 손실 함수 식의 값이 1.38 부근에 수렴해 가게 됨을 관찰할 수 있다. 그러면 학습이 잘 된 것이라 판단하면 된다. 다만 Keras에서는 GAN을 다른 방식으로 구현하기 때문에, 그 때의 loss값은 1.38과 관련이 없다.

둘째, G의 경우, V(D, G)를 minimize하기 위해 손실 함수의 그래디언트를 descending시키는 방향으로 학습한다.

다만, G의 손실 함수를 다음과 같이 minimization에서 Maximization 문제로 바꾸기도 한다.

\[\max_{G} = E_{z \tilde \ P_{z}(z)}[logD(G(z)]\]

어차피 로그 함수 형태를 생각하면 둘 다 같은 원리이다. 다만, 0부터 1 사이 구간에서 로그 함수의 그래디언트 변화 양상이 다르기 때문에, 이렇게 바꾸었을 때 초기 학습 효과가 개선된다. _{조삼모사 같지만 원숭이들이 현명했다는 강사님의 띵언…}

In practice, equation 1 may not provide sufficient gradient for G to learn well. Early in learning, when G is poor, D can reject samples with high confidence because they are clearly different from the training data. In this case, log(1−D(G(z))) saturates. Rather than training G to minimize log(1−D(G(z))) we can train G to maximize logD(G(z)). This objective function results in the same fixed point of the dynamics of G and D but provides much stronger gradients early in learning.

셋째, 한 학습의 epoch은 2-step으로 D를 학습시키고 G를 학습시키는 것으로 정의된다. 이 때 한 epoch 내에서 D를 k번 학습시킨 뒤, G를 1번 학습시킨다. 그러나 논문의 저자 여기 편의상 k=1로 설정한다고 한다. 즉, D를 1번 학습시키고 G를 1번 학습시킨다.

4. 결과

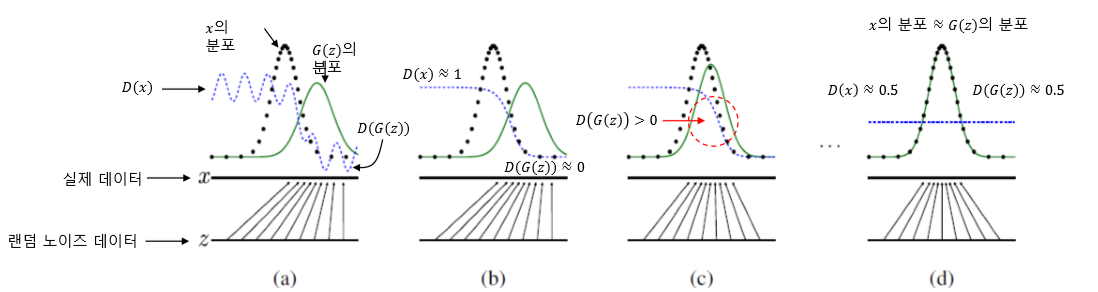
학습이 진행되기 전 (a) 상태를 보자. 실제 데이터 x가 정규 분포 형태를 갖고, 랜덤 데이터 z를 나타냈을 때 위와 같은 분포를 갖는다고 하자.

초기에는 D가 출력해 내는 값이 0과 1로 비교적 잘 구분된다. 그래프 D(x)와 D(G(z))의 분포를 보면, 원래 x의 분포 영역에서는 1에 가까운 값이, G(z)의 분포 영역에서는 0에 가까운 값이 나온다. 두 분포가 겹치는 구역에서는 그래프가 0과 1사이의 영역에 존재한다.

(b)와 (c) 단계는 G가 학습하는 과정을 나타낸다. 상술했듯, 학습을 통해 결과적으로 G가 원래 데이터의 분포를 모방한 분포를 생성해 내기 때문에, G(z)가 점차 원래 데이터의 분포를 닮아 간다. D(G(z))의 값이 점차 커지고, D(x)의 값이 작아지는 것을 그래프로 확인할 수 있다.

학습이 완료된 (d) 단계에서는 마침내 G(z)의 분포와 x의 분포가 동일해지게 된다. D(x)와 D(G(z))도 0.5로 수렴한다. 즉, 임의의 랜덤 데이터를 G에 입력하면 x와 유사한 분포 특성을 갖는 데이터가 출력되며, D는 어떤 데이터가 들어오든 이를 구분하지 못하게 된다!