[DL] GAN_2.구현_정규분포 1

6 분 소요

^{조성현 강사님의 강의 및 강의 자료를 기반으로 합니다.} ^{Github Repo}

^{Tensorflow : 2.2.0}

GAN 구현-정규분포-Tensorflow

1. 모델 아키텍쳐

Tensorflow에서 GAN 모델을 구현하는 것은 비교적 간단하다. 구현할 모델의 아키텍쳐를 간단히 나타내면 다음과 같다.

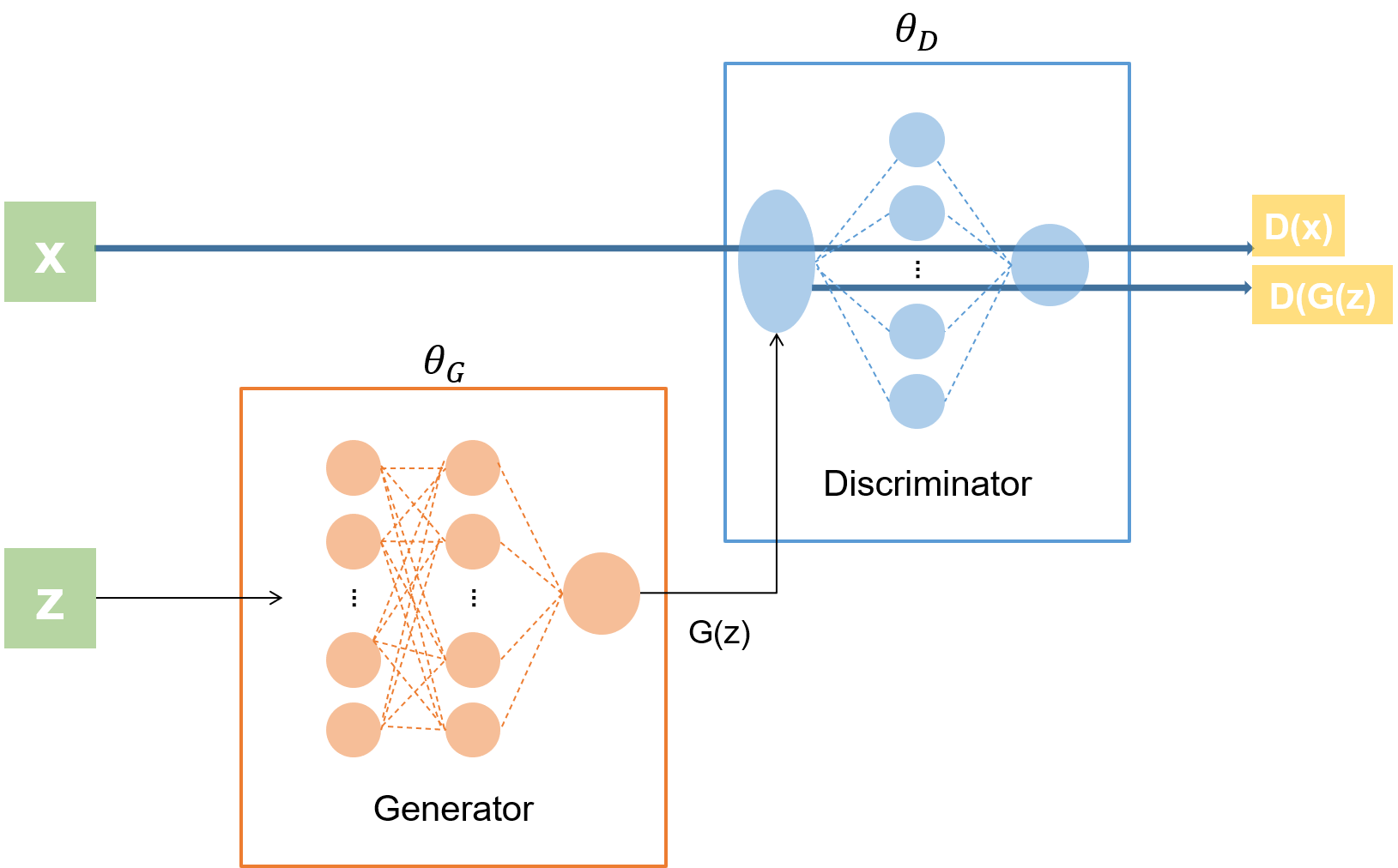
GAN-TF

진짜 데이터 x와 가짜 데이터 z가 있고, G가 가짜 데이터로부터 특정 확률 분포를 따르는 G(z)를 만들어 낸다. x와 G(z)가 D로 입력된다.

모델을 설계할 때 가장 중요한 것은 다음의 두 가지이다.

D의 출력 노드는 무조건 1개이며, 활성화 함수는 sigmoid이다.
G의 출력 노드는 D의 입력 노드 수와 같아야 한다. G의 출력을 통해 만들어진 가짜 데이터가 D로 입력되기 때문이다.

2. 구현

정규분포를 따르는 실제 데이터 x를 샘플링한다. -1과 1 사이의 uniform 분포로부터 아무 데이터 z를 샘플링하고, G가 x의 분포를 모방한 분포를 만들어내도록 한다. low-level 코딩에서 GAN 모델의 알고리즘이 어떻게 수식 및 레이어로 변환되는지에 중점을 맞추어 살펴 보자.

# 모듈 불러오기
import numpy as np
import tensorflow as tf
from tensorflow.keras.optimizers import Adam
import matplotlib.pyplot as plt
import seaborn as sns

# 1) 실제 데이터 준비
real_data = np.random.normal(size=1000).astype(np.float32)
real_data = real_data.reshape(real_data.shape[0], 1)
real_data_batch = tf.data.Dataset.from_tensor_slices(real_data)\
			.shuffle(buffer_size=real_data.shape[0])\
    			.batch(batch_size=300)

# 2) KL Divergence 계산 함수
def calc_KL(P, Q):
    hist_P, bins_P = np.histogram(P)
    hist_Q, bins_Q = np.histogram(Q)
    
    # 확률 분포 정규화
    pdf_P = hist_P / (np.sum(hist_P) + 1e-8)
    pdf_Q = hist_Q / (np.sum(hist_Q) + 1e-8)
    
    # KL Divergence 공식에 맞춰 계산
    kld_PQ = np.sum(pdf_P * (np.log(pdf_P + 1e-8) - np.log(pdf_Q + 1e-8)))
    
    return pdf_P, pdf_Q, kld_PQ

# log 클리핑
def clip_log(x):
    return tf.math.log(x + 1e-8)

# 3) Discriminator 네트워크 설정
d_input = real_data.shape[1]
d_hidden = int(input('Discriminator 은닉 노드 수 설정: '))
d_output = 1 # 주의

d_Wh = tf.Variable(tf.random.normal(shape=[d_input, d_hidden]), name='D_hidden_weight')
d_Bh = tf.Variable(tf.random.normal(shape=[d_hidden]), name='D_hidden_bias')
d_Wo = tf.Variable(tf.random.normal(shape=[d_hidden, d_output]), name='D_output_weight')
d_Bo = tf.Variable(tf.random.normal(shape=[d_output]), name='D_output_bias')

theta_D = [d_Wh, d_Bh, d_Wo, d_Bo]

# 4) Generator 네트워크 설정
g_input = int(input('Generator 입력 노드 수 설정: '))
g_hidden = int(input('Generator 은닉 노드 수 설정: '))
g_output = d_input # 주의

g_Wh = tf.Variable(tf.random.normal(shape=[g_input, g_hidden]), name='G_hidden_weight')
g_Bh = tf.Variable(tf.random.normal(shape=[g_hidden]), name='G_hidden_bias')
g_Wo = tf.Variable(tf.random.normal(shape=[g_hidden, g_output]), name='G_output_weight')
g_Bo = tf.Variable(tf.random.normal(shape=[g_output]), name='G_output_bias')

theta_G = [g_Wh, g_Bh, g_Wo, g_Bo]

# 5) Discriminator 함수
def Discriminator(data):
    d_Hidden = tf.nn.relu(tf.matmul(data, d_Wh) + d_Bh)
    d_Out = tf.nn.sigmoid(tf.matmul(d_Hidden, d_Wo) + d_Bo)
    return d_Out

# 6) Generator 함수
def Generator(data):
    g_Hidden = tf.nn.relu(tf.matmul(data, g_Wh) + g_Bh)
    g_Out = tf.matmul(g_Hidden, g_Wo) + g_Bo # 주의
    return g_Out

# 가짜 데이터 생성
def makeZ(m, n=g_input):
    z = np.random.uniform(-1.0, 1.0, size=[m,n]).astype(np.float32)
    return z

# 7) Discriminator loss 함수
def loss_Discriminator(x, z):
    Dx = Discriminator(x) # Discriminator가 판별한 x 데이터
    Gz = Generator(z) # Generator가 z로 만들어 낸 데이터
    DGz = Discriminator(Gz) # Discriminator가 판별한 Gz 데이터
    
    loss = tf.reduce_mean(clip_log(Dx) + clip_log(1-DGz))
    return -loss

# 8) Generator loss 함수
def loss_Generator(z):
    Gz = Generator(z)
    DGz = Discriminator(Gz)
    
    loss = tf.reduce_mean(clip_log(1-DGz))
    return loss 

# 9) 학습
opt = Adam(learning_rate=0.0005)

loss_D_hist = []
loss_G_hist = []
KLdivergence_hist = []

EPOCHS = int(input('학습 횟수 설정: '))

for epoch in range(EPOCHS): 
    for X_batch in real_data_batch: # 미니 배치 업데이트
        Z_batch = makeZ(m=X_batch.shape[0], n=g_input)        
        
        opt.minimize(lambda: loss_Discriminator(X_batch, Z_batch), var_list=theta_D)
        opt.minimize
    
    if epoch % 10 == 0:
        loss_D_hist.append(loss_Discriminator(X_batch, Z_batch))
        loss_G_hist.append(loss_Generator(Z_batch))
        P, Q, kld = calc_KL(X_batch, Generator(Z_batch))
        KLdivervenge_hist.append(kld)
        
        print("Epoch %d : loss-D %.4f, loss-G %.4f, KLdivergence: %.4f" % (epoch, loss_D_hist[-1], loss_G_hist[-1], kld))
        

# loss 시각화
plt.figure(figsize=(6, 4))
plt.plot(loss_D_hist, label='Discriminator Loss', color='red')
plt.plot(loss_G_hist, label='Generator Loss', color='blue')
plt.title('Loss History', size=18)
plt.legend()
plt.grid()
plt.show()

# KLdivergence 시각화
plt.figure(figsize=(6, 4))
plt.plot(KLdivergence_history, label='KL Divergence', color='green')
plt.legend()
plt.grid()
plt.show()

# 학습 완료 후 가짜 데이터 생성해 시각화
z = makeZ(m=real_data.shape[0], n=g_input)
fake_data = Generator(z).numpy() # Tensor -> Numpy array 형태
plt.figure(figsize=(8, 5))
sns.set_style('whitegrid')
sns.kdeplot(real_data[:, 0], color='blue', bw=0.5, label='REAL data')
sns.kdeplot(real_data[:, 1], color='red', bw=0.3, label='FAKE data')
plt.title('REAL vs. FAKE distribution')
plt.legend()
plt.show()

# 학습 완료 후 real data와 fake data 넣었을 때 어떻게 달라지는가?
d_real_values = Discriminator(real_data) # 실제 데이터 판별값
d_fake_values = Discriminator(fake_data) # 가짜 데이터 판별값
print(d_real_values[:10])
print(d_fake_values[:10])

plt.figure(figsize=(8, 5))
plt.plot(d_real_values, label='Discriminated Real Data')
plt.plot(d_fake_values, label='Discriminated Fake Data', color='red')
plt.legend()
plt.show()

1) 실제 데이터 준비

표준 정규분포로부터 1000개의 데이터를 무작위로 샘플링한다. 이를 2차원 형태로 만들어 신경망에 입력할 수 있도록 만든다. 이후 300개씩 미니배치 업데이트할 수 있도록 배치 데이터셋으로 만들어 준다.

2) KL Divergence 계산

사실 GAN 네트워크 구현 자체에서 큰 역할을 하지는 않으나, 강사님께서 연습 삼아 넣은 함수이다. P, Q의 데이터를 histogram으로 만들고, 면적으로 나누어 정규해 pdf로 만든다. 면적으로 나눌 때 분모가 0이 되는 것을 방지하기 위해 1e-8을 더한다.

이후 공식에 맞춰 KL Divergence를 계산한다. 나중에 분포가 얼마나 다른지 수치화하여 확인하기 위한 용도이다.

3), 4) 네트워크 설정

상술했던 주의 사항을 지켜 노드 수를 설정한다. 구현 단계에서는 d_hidden을 8, g_input과 g_hidden을 각각 8, 4로 설정했다. 이처럼 D의 은닉층 노드 수와 G의 입력 및 은닉층 노드 수는 마음대로 설정해도 된다.

이후 학습 시 업데이트 할 가중치를 모두 theta로 묶는다.

5), 6) Discriminator, Generator 구현

D와 G가 데이터를 받아 각각 판별하고, 가짜 데이터를 생성해 내는 함수이다. 둘 모두 은닉층에서는 활성화 함수로 ReLU를 사용한다. Discriminator의 경우 출력층의 활성화 함수가 sigmoid이고, Generator 함수의 경우 출력값이 그대로 D의 입력으로 사용되므로 활성화 함수가 없음 에 주의한다.

7), 8) loss 함수 구현

앞에서 공부한 D와 G의 loss 함수를 코드로 짜면 된다. D의 loss 함수를 minimization 문제로 바꿔 주었다. 둘 모두 log의 진수 값이 0이 되는 것을 방지하기 위해 위에서 정의한 clip_log 함수를 사용해 주었다.

9) 학습

총 학습 에폭 수를 3000회로 설정했다.

1에폭 안의 학습에서 배치 데이터셋으로부터 데이터를 미니 배치 단위(300개)로 넣는다. 미니 배치 데이터 개수만큼 Z 데이터를 생성한다. Adam 옵티마이저를 사용해 D를 먼저 학습하고, 이후 G를 학습한다. 이렇게 미니 배치 단위로 모든 데이터가 입력되고, 가중치가 업데이트 되면 한 에폭의 학습이 끝난 것이다. 이제 10번의 에폭마다 loss, kld를 계산하고 기록한다.

3. 결과

3.1. 기록 확인

기록한 loss 값이 어떻게 변화하는지 추이를 살펴 보자.

Epoch 0 : loss-D 2.5732, loss-G -2.3189, KL-Divergence 1.3767
Epoch 10 : loss-D 2.8022, loss-G -2.5210, KL-Divergence 1.2271
Epoch 20 : loss-D 2.9383, loss-G -2.6476, KL-Divergence 1.1660
Epoch 30 : loss-D 2.8318, loss-G -2.5562, KL-Divergence 0.5509
Epoch 40 : loss-D 2.7600, loss-G -2.5106, KL-Divergence 0.5373
Epoch 50 : loss-D 2.7389, loss-G -2.4951, KL-Divergence 0.2335
Epoch 60 : loss-D 2.5800, loss-G -2.3613, KL-Divergence 0.3635
Epoch 70 : loss-D 2.4390, loss-G -2.2286, KL-Divergence 0.5460
Epoch 80 : loss-D 2.3438, loss-G -2.1425, KL-Divergence 0.5518
Epoch 90 : loss-D 2.0461, loss-G -1.8677, KL-Divergence 0.2627
Epoch 100 : loss-D 1.9032, loss-G -1.7259, KL-Divergence 0.2256
    
(...)

Epoch 2930 : loss-D 1.3758, loss-G -0.7031, KL-Divergence 0.2272
Epoch 2940 : loss-D 1.3958, loss-G -0.7204, KL-Divergence 0.1772
Epoch 2950 : loss-D 1.3843, loss-G -0.6645, KL-Divergence 0.0880
Epoch 2960 : loss-D 1.3896, loss-G -0.6843, KL-Divergence 0.1881
Epoch 2970 : loss-D 1.3844, loss-G -0.7167, KL-Divergence 0.0811
Epoch 2980 : loss-D 1.3846, loss-G -0.7053, KL-Divergence 0.1524
Epoch 2990 : loss-D 1.3736, loss-G -0.6263, KL-Divergence 0.3755

Discriminator의 loss 값이 점차 줄어 1.38에 수렴해 가고 있는 것을 확인할 수 있다. 참고로 확인한 KL divergence 값 역시 초반에 비해 많이 줄어든다. 다만, loss 값처럼 수렴하지는 않고 커졌다 작아졌다 하는 양상을 보인다.

Loss	KL divergence

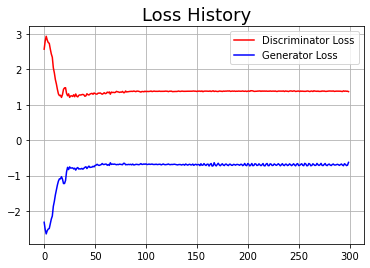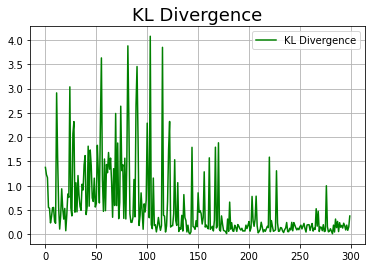3.2. Generator가 만들어 낸 분포 확인

학습 과정을 거쳤기 때문에 G는 어떤 데이터를 받더라도 실제 데이터의 분포를 모사해 낸 분포를 만들어 낼 것이다. 진짜인지 확인하기 위해 임의의 가짜 데이터를 생성한 뒤, Generator 함수에 통과시켜 분포를 확인하자.

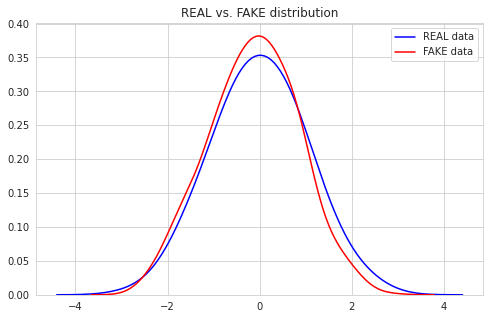
3.3. Discriminator의 판단 확인

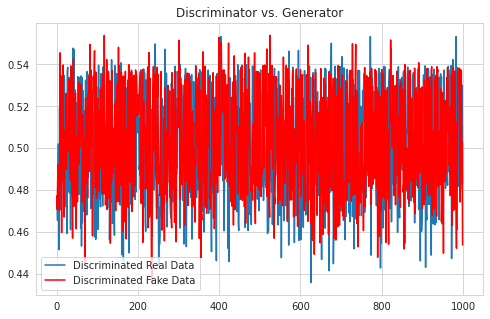
마지막으로 학습 과정이 완료된 상태에서 D의 판별이 어떻게 달라지는지 확인하자. 실제 데이터 real_data와 fake_data를 Discriminator 함수에 통과시킨다. 각각의 결과를 확인하면 다음과 같이 어떤 경우든 0.5의 값이 많이 출력되는 것을 확인할 수 있다.

# real_data 10개 판별
tf.Tensor(
[[0.4773296 ]
 [0.4727556 ]
 [0.46554345]
 [0.48083037]
 [0.5020013 ]
 [0.4765454 ]
 [0.45154893]
 [0.51942885]
 [0.48934934]
 [0.5139421 ]], shape=(10, 1), dtype=float32)

# fake_data 10개 판별
tf.Tensor(
[[0.4769391 ]
 [0.47082454]
 [0.4811762 ]
 [0.49221426]
 [0.49147302]
 [0.4757505 ]
 [0.47056288]
 [0.47033453]
 [0.5455954 ]
 [0.5300759 ]], shape=(10, 1), dtype=float32)

그림으로 확인해 보더라도, 실제로 0.5 부근에서 판별 값의 분포가 형성된다. 심지어, 그 양상마저 비슷하다!

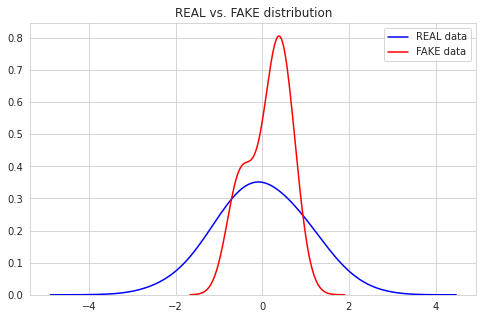
3.4. 학습이 제대로 되지 않았을 경우

처음에 옵티마이저의 학습률을 0.05로 설정했더니, 학습이 제대로 되지 않았다. 이 경우 분포가 어떻게 형성되는지 확인하자.

Twitter Facebook LinkedIn

이레이저

[DL] GAN_2.구현_정규분포 1

GAN 구현-정규분포-Tensorflow

1. 모델 아키텍쳐

2. 구현

3. 결과

3.1. 기록 확인

3.2. Generator가 만들어 낸 분포 확인

3.3. Discriminator의 판단 확인

3.4. 학습이 제대로 되지 않았을 경우

공유하기

댓글남기기

참고

[Go] gin validator 에러 메시지 변경

[AI] SlowFast Demo 실행

[AI] DL GPU 개발환경 구축 - WSL

[k8s] Kubernetes 환경에서 Argo Workflow Artifact 기능 사용하기