[DL] GAN_2.구현_정규분포 2
조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo
Tensorflow : 2.2.0
GAN 구현-정규분포-Keras
1. 모델 아키텍쳐
Keras에서 functional API를 이용해 GAN 모델을 구현한다. 본래 Keras의 경우 Supervised Learning 방식의 모델 설계에 특화되어 있기 때문에, Unsupervised Learning 방식의 GAN 모델을 설계하기 위해서는 labeling을 통해 Supervised Learning 방식의 이진 분류 문제로 바꿔 주어야 한다
구현할 모델의 아키텍쳐를 나타내면 다음과 같다.
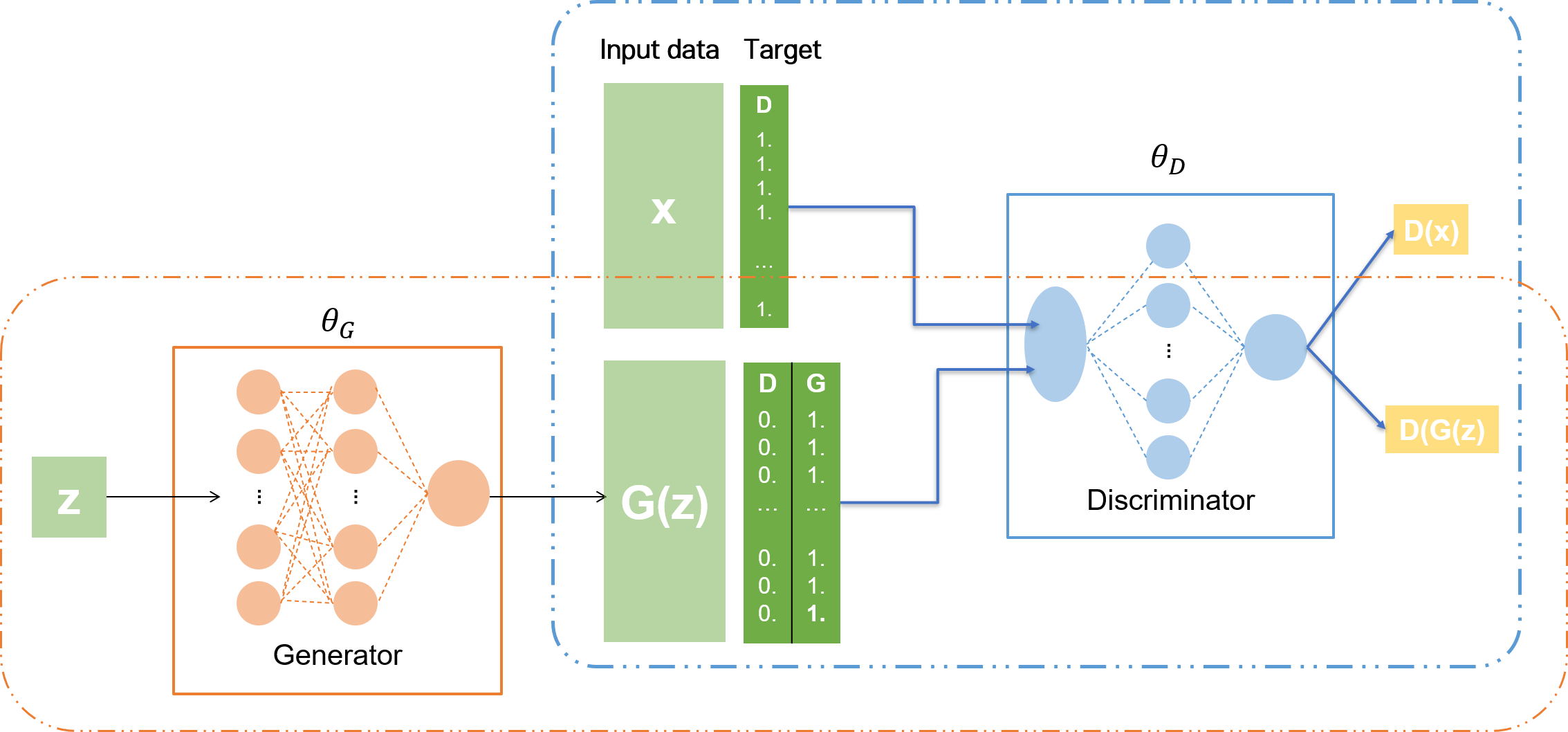
Tensorflow 구현과 달라지는 점은 크게 다음과 같다.
첫째, 학습 데이터를 만든다. 실제 데이터(real_data)와 가짜 데이터(fake_data)를 따로 만들고, 여기다가 라벨을 붙인다. Discriminator가 학습할 라벨은 real_data가 1.0, fake_data가 0.0이다. 반면 Generator는 fake_data를 만들어 내고, Discriminator로 하여금 fake_data에 대한 출력값이 1.0이 나오도록 방해한다.
둘째, loss function이 사라진다. 이진 분류 문제로 바꿔 주는 순간, 논문에서 제안한 GAN 모델의 loss function을 사용하지 않아도 된다. 일반적으로 이진 분류 문제에서 사용하는 binary crossentropy 함수를 loss function으로 사용하면 된다.
셋째, 네트워크 구조가 달라진다. Discriminator 모델과 Generator 모델을 만든다. 두 모델은 각각 Tensorflow에서 구현한 것과 같이 레이어로 이루어져 있다. 그리고 두 모델을 연결한 GAN 모델을 만든다. GAN은 두 모델을 연결하는 네트워크이기 때문에, 레이어가 아니라 모델로 구성되어 있다. 각각의 작동 방식은 다음과 같다.
Discriminator모델은Discriminator모델 네트워크 내에서 학습한다.Generator모델은 가짜 데이터를 만들어 내기만 한다.GAN네트워크는Discriminator와Generator를 입력으로 받고, 두 네모델을 연결한 후, 원하는 목적을 달성하도록Generator만 학습시킨다.
Keras에서 구현하는 방식을 보니 확실히 GAN 모델의 승자는
G라는 것이 실감이 나는 듯하다. GAN 네트워크를 빌드할 때 핵심은D가 아니라G이다.
넷째, 에폭 설정 및 배치 구현이 달라진다. 기존에 Keras에서 에폭을 설정하던 방식으로 에폭을 설정하면, D 100번, GAN 100번의 방식으로 학습이 이루어진다. 따라서 반복문을 통해 D 가중치 1번 업데이트, G 가중치 1번 업데이트가 이루어지도록 하고, 그 안에서 직접 미니 배치를 수동으로 구현해 주어야 한다. 첫째에서 기술한 학습 데이터 생성 역시 미니 배치를 구현하는 현재 단계에서 이루어진다.
2. 구현
Keras에서 GAN 모델 구현하는 데에 집중하기 위해, KL Divergence는 계산하지 않는다. 노드 수 설정 등은 Tensorflow로 구현했을 때와 비슷하다. 옵티마이저, 학습률 등은 강사님께서 참고하신 소스에서 성능이 좋은 것이라 하므로, 지금 단계에서 집중하지는 않고, 나중에 바꿔보도록 한다.
# 모듈 불러오기
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.models import Model
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras import backend as K
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import tensorflow as tf
# 5) eager execution 기능 끄기
tf.compat.v1.disable_eager_execution()
# 실제 데이터 준비
real_data = np.random.normal(size=1000)
real_data = real_data.reshape(real_data.shape[0], 1)
# 가짜 데이터 생성
def makeZ(m, n):
z = np.random.uniform(-1.0, 1.0, size=[m, n])
return z
# 모델 파라미터 설정
d_input = real_data.shape[1]
d_hidden = 32
d_output = 1 # 주의
g_input = 16
g_hidden = 32
g_output = d_input # 주의
# 옵티마이저 설정
def myOptimizer(lr):
return RMSprop(learning_rate=lr)
# 1) Discriminator 모델
def build_D():
d_x = Input(batch_shape=(None, d_input))
d_h = Dense(d_hidden, activation='relu')(d_x)
d_o = Dense(d_output, activation='sigmoid')(d_h)
d_model = Model(d_x, d_o)
d_model.compile(loss='binary_crossentropy', optimizer=myOptimizer(0.001))
return d_model
# 2) Generator 모델
def build_G():
g_x = Input(batch_shape=(None, g_input))
g_h = Dense(g_hidden, activation='relu')(g_x)
g_o = Dense(g_output, activation='linear')(g_h) # 주의
g_model = Model(g_x, g_o) # 주의
return g_model
# 3) GAN 네트워크
def build_GAN(discriminator, generator):
discriminator.trainable = False # discriminator 업데이트 해제
z = Input(batch_shape=(None, g_input))
Gz = generator(z)
DGz = discriminator(Gz)
gan_model = Model(z, DGz)
gan_model.compile(loss='binary_crossentropy', optimizer=myOptimizer(0.0005))
return gan_model
# 4) 학습
K.clear_session() # 5) 그래프 초기화
D = build_D() # discriminator 모델 빌드
G = build_G() # generator 모델 빌드
GAN = build_GAN(D, G) # GAN 네트워크 빌드
n_batch_cnt = int(input('입력 데이터 배치 블록 수 설정: '))
n_batch_size = int(real_data.shape[0] / n_batch_cnt)
EPOCHS = int(input('학습 횟수 설정: '))
for epoch in range(EPOCHS):
# 미니배치 업데이트
for n in range(n_batch_cnt):
from_, to_ = n*n_batch_size, (n+1)*n_batch_size
if n == n_batch_cnt -1 : # 마지막 루프
to_ = real_data.shape[0]
# 학습 데이터 미니배치 준비
X_batch = real_data[from_: to_]
Z_batch = makeZ(m=X_batch.shape[0], n=g_input)
Gz = G.predict(Z_batch) # 가짜 데이터로부터 분포 생성
# discriminator 학습 데이터 준비
d_target = np.zeros(X_batch.shape[0]*2)
d_target[:X_batch.shape[0]] = 0.9
d_target[X_batch.shape[0]:] = 0.1
bX_Gz = np.concatenate([X_batch, Gz]) # 묶어줌.
# generator 학습 데이터 준비
g_target = np.zeros(Z_batch.shape[0])
g_target[:] = 0.9 # 모두 할당해야 바뀜.
# discriminator 학습
loss_D = D.train_on_batch(bX_Gz, d_target) # loss 계산
# generator 학습
loss_G = GAN.train_on_batch(Z_batch, g_target)
if epoch % 10 == 0:
z = makeZ(m=real_data.shape[0], n=g_input)
fake_data = G.predict(z) # 가짜 데이터 생성
print("Epoch: %d, D-loss = %.4f, G-loss = %.4f" %(epoch, loss_D, loss_G))
# 학습 완료 후 데이터 분포 시각화
z = makeZ(m=real_data.shape[0], n=g_input)
fake_data = G.predict(z)
plt.figure(figsize=(8, 5))
sns.set_style('whitegrid')
sns.kdeplot(real_data[:, 0], color='blue', bw=0.3, label='REAL data')
sns.kdeplot(fake_data[:, 0], color='red', bw=0.3, label='FAKE data')
plt.legend()
plt.title('REAL vs. FAKE distribution')
plt.show()
# 학습 완료 후 discriminator 판별 시각화
d_real_values = D.predict(real_data) # 실제 데이터 판별값
d_fake_values = D.predict(fake_data) # 가짜 데이터 판별값
plt.figure(figsize=(8, 5))
plt.plot(d_real_values, label='Discriminated Real Data')
plt.plot(d_fake_values, label='Discriminated Fake Data', color='red')
plt.title("Discriminator vs. Generator")
plt.legend()
plt.show()
1), 2) Discriminator, Generator 모델 빌드
각 모델을 빌드한다. 은닉층 활성화 함수, 출력층 활성화 함수 모두 Tensorflow 구현과 동일하다. 다만, Tensorflow에서 Generator 출력층에 활성화 함수를 적용하지 않았던 것이 Keras에서는 linear 함수로 바뀌었음에 주의한다.
Discriminator는 모델을 빌드하면서 바로 학습한다. 따라서 모델 빌드 함수 내에서 compile한다. 이진 분류 문제로 변형해서 풀기 때문에, loss 함수는 binary crossentropy가 된다. Generator는 Discriminator 학습이 완료된 후, 뒤에 빌드할 GAN 네트워크에서 compile 한다.
3) GAN 네트워크 빌드
Generator와 Discriminator를 이어 준다. Discriminator가 DGz를 판별할 때 1에 가까운 값이 나오도록 해야 한다. 여기서 Discriminator는 학습되지 않는다. Generator만 학습시킨다. 따라서 가중치 업데이트가 Discriminator에 전달되지 않도록, Discriminator를 freeze한다. trainable = False 옵션으로 구현한다. 그리고 모델을 compile 한다.
4) 학습
먼저 미니 배치 업데이트를 위해 배치 사이즈를 설정해 데이터를 불러 온다. n_batch_cnt로 배치 횟수를 설정하고, n_batch_size에 배치 사이즈를 설정한다. from_, to_를 사용해 데이터를 끊어서 가져온다. 이 때, 마지막 배치에서는 끝의 데이터까지 모두 가져오도록 조건을 설정한다. (PyTorch의 drop_last 옵션이랑 비슷한 듯?)
배치 사이즈를 설정한 뒤, 학습 데이터를 준비한다. 가져 온 X_batch와 같은 개수의 가짜 데이터 Z_batch를 만든다. 빌드한 Generator가 Keras의 모델 객체이므로, .predict를 사용해야 데이터가 만들어 진다!
이제 각 모델이 학습할 데이터셋을 만든다. Discriminator의 경우 실제 데이터 X_batch와 가짜 데이터 Z_batch를 모두 입력으로 받아야 하므로, 두 데이터를 묶어 준다. 이와 쌍이 되는 라벨의 경우 X_batch에 대해 0.9를, Z_batch에 0.1을 할당한다. 1.0이나 0.0을 할당하지 않는 이유는, 1.0이나 0.0보다 0.9, 0.1의 약간은 벗어난(?) 값을 설정할 때 더 학습 성능이 좋다고 알려졌기 때문이라고. Generator의 경우도 똑같다. 그러나 Z_batch에 대해서 만, 라벨을 0.9로 설정한다는 점에만 주의하자.
학습하고 loss를 계산한다. 이 때 .fit이 아니라 .train_on_batch를 사용한다. .fit은 에폭과 batch_size마다 연산을 한다. 반면 .train_on_batch는 batch마다 연산을 한다. 후자의 연산 속도가 더 빠르다.
참고
단순히 연산 속도만 차이가 있을까 싶어 documentation을 살펴 보았다.
fit
fit(x=None, y=None, batch_size=None, epochs=1, verbose=1, callbacks=None, validation_split=0.0, validation_data=None, shuffle=True, class_weight=None, sample_weight=None, initial_epoch=0, steps_per_epoch=None, validation_steps=None)정해진 수의 세대에 걸쳐 모델을 학습시킵니다 (데이터셋에 대해 반복).
- batch_size: 정수 혹은
None. 경사 업데이트 별 샘플의 수. 따로 정하지 않으면,batch_size는 디폴트 값인 32가 됩니다.- epochs: 정수. 모델을 학습시킬 세대의 수. 한 세대는 제공된 모든
x와y데이터에 대한 반복입니다.initial_epoch이 첫 세대라면,epochs는 “마지막 세대”로 이해하면 됩니다. 모델은epochs에 주어진 반복의 수만큼 학습되는 것이 아니라, 단지epochs색인의 세대에 도달할 때까지 학습됩니다.train_on_batch
train_on_batch(x, y, sample_weight=None, class_weight=None)하나의 데이터 배치에 대해서 경사 업데이트를 1회 실시합니다.
물론
fit의 경우epoch과batch_size를 모두 받고,train_on_batch의 경우 한 번의 배치에 대해서만 그래디언트를 계산하기 때문에 연산이 빠르다. 그러나 연산 속도 측면 외에 논리적으로도 배치 사이즈마다 GAN 모델이 데이터를 넘겨 받고, 그 배치 사이즈의 데이터가 업데이트될 때마다 모델이 업데이트되도록 구성했기 때문에, 후자를 사용하는 것이 더 맞다고 판단된다.
5) Keras 기능 주의
이전에는 사용하지 않던 기능을 두 가지 사용했다.
첫째, eager_execution 기능을 해제했다. Tensorflow 2.x 버전으로 넘어 오면서 Session 객체를 없애고, 그래프 생성과 동시에 실행되도록 하는 eager_execution 모드를 사용한다. 그러나 위에서 구성한 코드는 반복문을 통해 에폭을 구현하고, 한 에폭 안에서 배치 사이즈마다 train_on_batch를 통해 그래프를 계속해서 그리고 동시에 실행해야 한다. 결과적으로, 속도가 늦어진다. 따라서 1.x 버전에서처럼 그래프 객체를 모두 생성해 놓고, 그 안에서 실행하도록 잠시 eager mode 기능을 해제한다.
둘째, clear_session 기능을 사용했다. (예전에 문쌤이랑 했을 때 eager mode 해제하고, 계속 실행하다 보면 이전 결과가 남아 있어서 그래프가 제대로 그려지지 않을 수 있으므로, backend 기능을 사용해 실행할 때마다 global_variables_initializer()이랑 비슷한 듯)안전하게 세션을 정리해 주자.
이 코드 없으면 어떻게 되는지 확인해 보고 싶다면, 실제로 주석 처리하고 실행하면서 모델 summary를 확인해 보자. layer 뒤에 붙는 수가 계속해서 커진다!
3. 결과
Tensorflow 구현에서와 달리 loss 값이 특정 값으로 수렴했을 때 학습이 잘 된다는 기준은 없다. loss function이 binary crossentropy이기 때문이다. 그래프로 시각화한 결과를 통해 Generator가 잘 모방하고 있고, Discriminator가 제대로 판별하지 못하고 있음을 확인할 수 있다.
| distribution | discriminated values |
|---|---|
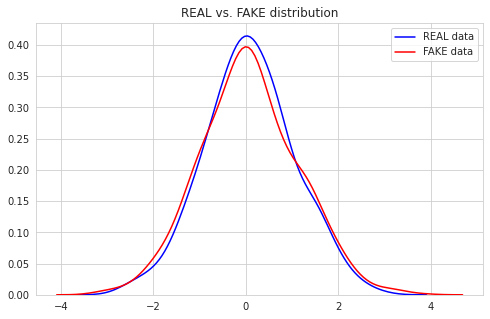 |
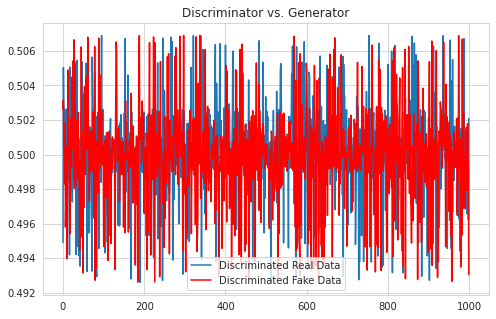 |
GAN 모델 구조만 확인해 보자. 모델 안에 모델이 들어 있다. 코드 상에서 가장 마지막에 빌드되는 모델이기 때문에, 모델의 순번이 2로 붙어 있음도 깨알 같이 기억하자.
Model: "model_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) [(None, 16)] 0
_________________________________________________________________
model_1 (Model) (None, 1) 577
_________________________________________________________________
model (Model) (None, 1) 97
=================================================================
Total params: 674
Trainable params: 577
Non-trainable params: 97
_________________________________________________________________
None
4. 변형
두 개의 정규 분포를 합쳤을 때 GAN 모델이 데이터를 잘 생성해내는지도 확인해 보자. 분포가 복잡해 졌기 때문에 노드 수만 조금 더 늘려서 네트워크를 복잡하게 구성했을 뿐, 나머지는 다 동일하다.
# 실제 데이터 준비
real_data_1 = np.random.normal(size=1000)
real_data_2 = np.random.normal(5, 2, size=1000) # 또 다른 분포
real_data = np.hstack([real_data_1, real_data_2]) # 분포 합치기
real_data = real_data.reshape(real_data.shape[0], 1)
분포가 달라졌기 때문에 어떻게 생겼는지 확인하면 다음과 같다.
| distribution | 합친 분포 |
|---|---|
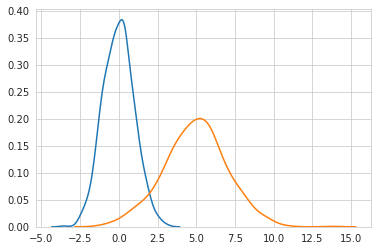 |
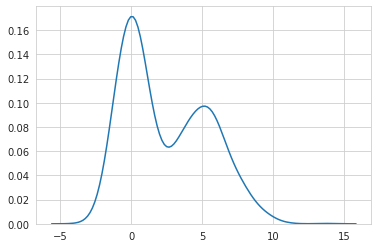 |
학습 횟수를 1500, 배치 블록 수를 5로 하여 학습한 결과이다. 모델 구조와 결과를 첨부한다.
Model: "model_2"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_3 (InputLayer) [(None, 32)] 0
_________________________________________________________________
model_1 (Model) (None, 1) 2177
_________________________________________________________________
model (Model) (None, 1) 193
=================================================================
Total params: 2,370
Trainable params: 2,177
Non-trainable params: 193
_________________________________________________________________
None
Model: "model_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_2 (InputLayer) [(None, 32)] 0
_________________________________________________________________
dense_2 (Dense) (None, 64) 2112
_________________________________________________________________
dense_3 (Dense) (None, 1) 65
=================================================================
Total params: 2,177
Trainable params: 2,177
Non-trainable params: 0
_________________________________________________________________
None
Model: "model"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_1 (InputLayer) [(None, 1)] 0
_________________________________________________________________
dense (Dense) (None, 64) 128
_________________________________________________________________
dense_1 (Dense) (None, 1) 65
=================================================================
Total params: 386
Trainable params: 193
Non-trainable params: 193
_________________________________________________________________
None
| distribution | discriminated values |
|---|---|
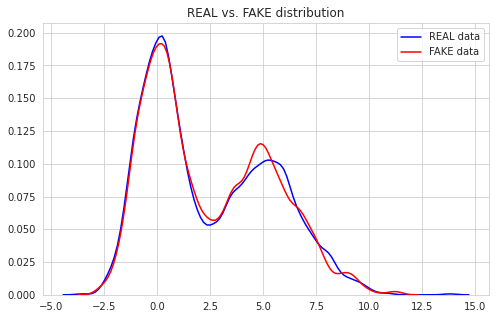 |
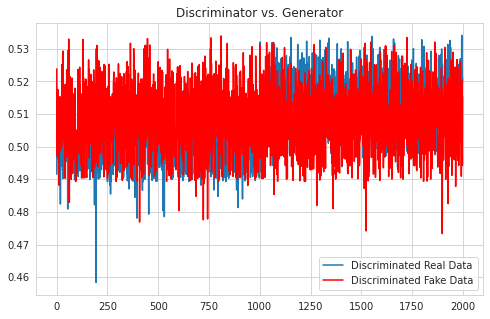 |


댓글남기기