[ML] KMeans_1.개념

^{출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다.}

^{Github Repo}

군집 분석(Clustering)은 각 데이터 간 특성에 따라 유사한 데이터를 ‘군집’으로 묶고, 각 군집 별로 특징을 분석하는 분석 방법이다. 정답에 해당하는 target class 없이 데이터 간 유사성을 바탕으로 군집으로 분류하기 때문에, 비지도 학습 방법이다. 대표적인 군집 분석의 알고리즘으로는 K-Means, H-Cluster, DBSCAN 등이 있다.

그 중에서도 가장 대표적인 K-Means 알고리즘에 대해 정리하고자 한다. 다른 클러스터링 기법에 대한 학습은 Github 저장소 및 강의 자료를 참고하자.

K-Means 알고리즘

1. 개념

K개의 중심점을 찍은 후, 중심점에서 각 점 간 거리의 합이 최소가 되는 중심점의 위치를 찾고, 그 점에서 가까운 점들을 묶는 클러스터링 알고리즘이다.

구체적인 수행 방식은 다음과 같다.

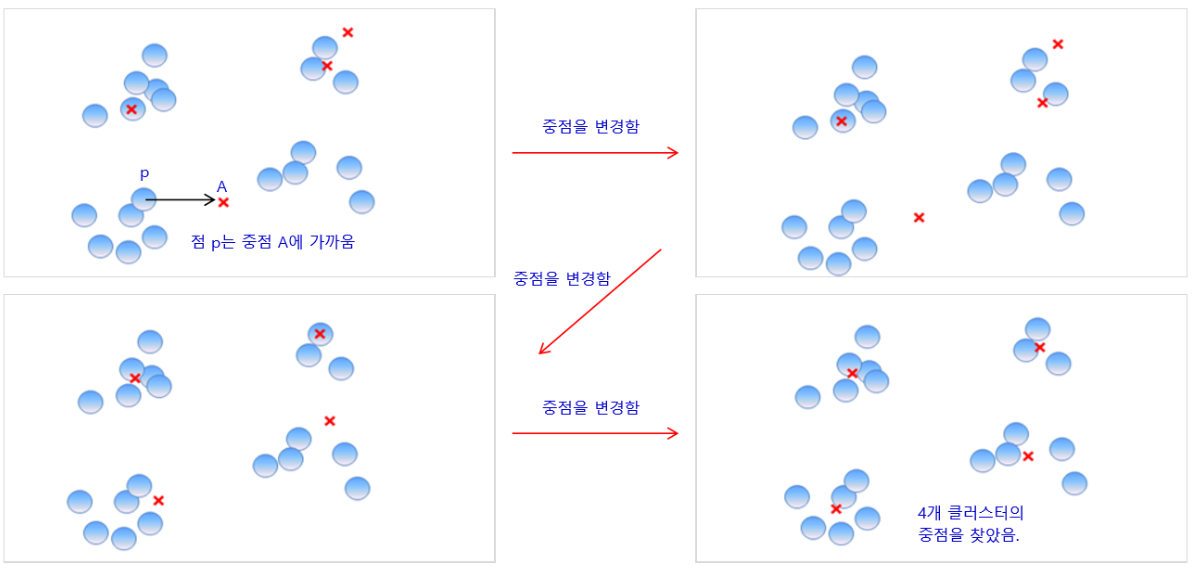
1. 분류할 군집의 수(K)를 결정한다.

2. K개의 초기 중점(Centroid)을 설정한다. 일반적으로는 임의의 방식으로 초기 중점을 선택한다.

3. 분류 대상이 되는 모든 데이터에 대해 가장 가까운 초기 중점을 찾아 cluster label을 부여한다.

4. 같은 cluster label을 가진 데이터의 평균 벡터를 구하여 초기 중점의 좌표를 변경(혹은 업데이트)한다.

5. 새로운 데이터가 들어오면, 군집 중점과의 거리를 계산하여 가장 가까운 군집의 라벨을 부여한다.

2.에서 4.에 해당하는 군집화 과정은 EM 알고리즘의 원리를 따른다. EM 알고리즘은 Expectation과 Maximization을 반복하며 수렴 조건을 만족하는 해를 찾아 나가는 방법인데, 그 자세한 수학적 원리까지는 들어가지 않는다.

이 알고리즘이 K-Means 클러스터링에 적용될 때, 찾고자 하는 최적의 해는 군집 중점의 좌표이다. 각 데이터에서 중점까지의 거리를 최소화하고자 하는 문제를 풀고자 한다. Expectation 단계에서 각 데이터를 군집에 가장 가까운 점에 할당하고, Maximization 단계에서 데이터와 할당된 중점까지의 거리를 계산하여 그 거리가 최소화되도록 군집의 중점을 변경 한다.

이렇게 중점의 좌표를 변경해 나가다, 중점의 좌표가 더 이상 변경되지 않는 때가 오면 수렴 조건을 만족했다고 보고, 그 지점을 클러스터의 중점 좌표로 설정한다.

참고

물론, 머신러닝 라이브러리에서 작동할 때에는 수렴 조건을 만족하지 않았더라도, 사용자가 정한 반복 수를 채우게 되면 좌표 업데이트 과정이 종료된다.

5.에 해당하는 예측 단계에서는 군집화 결과를 바탕으로 새로운 데이터와 군집 중점 간 거리를 계산하여 가장 가까운 군집으로 데이터를 할당한다.

2. 군집화 결과 측정

지도 학습과 달리 정답 라벨이 없기 때문에 오류 측정이 불가능하다. 이에 군집화 결과의 품질을 파악하기 위해 다음과 같은 방법이 고안되었다.

2.1. Elbow Method

각 데이터와 중점 까지의 거리 제곱합을 SSE로 사용한다. 클러스터 개수가 많아질수록 각 데이터와 할당된 군집 중점과의 거리 제곱합이 줄어드는 것은 당연하기 때문에, SSE의 감소율을 보고 군집화 결과를 판단한다. SSE의 감소 폭이 가장 줄어들 때의 군집화 품질이 좋다고 보는 것이다.

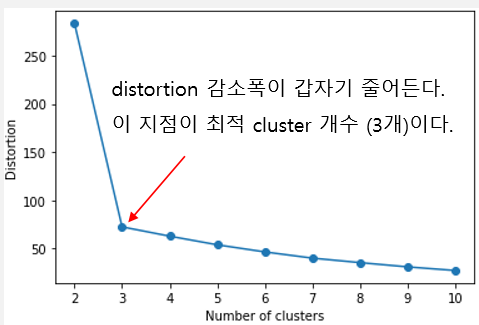
위와 같이 SSE의 감소 폭을 그래프를 통해 판단하면 그 모양이 팔꿈치와 비슷하다고 하여 Elbow Method(이것도 줄이면 EM…) 라고 한다.

2.2 Silhouette Method

군집 간에 분리가 잘 되어 있을수록 군집화 품질이 좋다는 아이디어에서 출발한다.

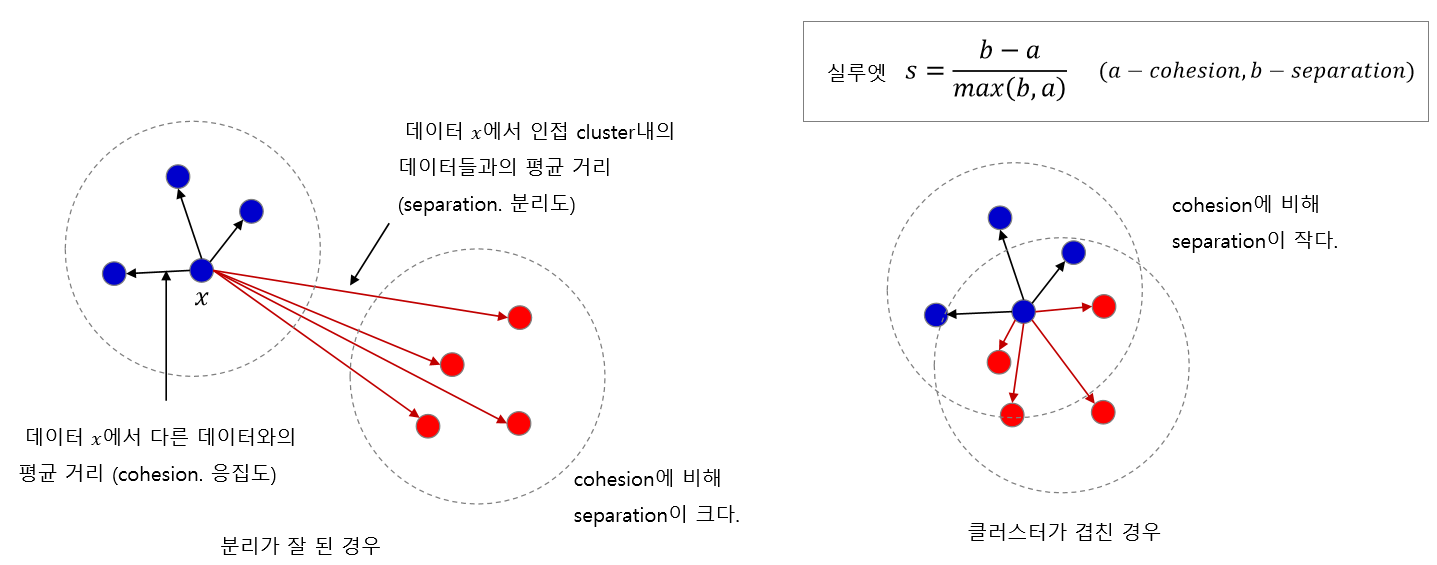
• 응집도(Cohesion)

임의의 데이터와 같은 군집 내에 속해 있는 다른 데이터 간 거리를 구한다. 직관적으로 판단할 때, 군집화가 잘 되어 있을 수록 이 거리는 짧아야 한다. 비슷한 데이터끼리 잘 뭉쳐 있을 것이기 때문이다.

이러한 관점에서 이 거리를 응집도라고 한다. 정확하게 정의하자면, 임의의 데이터 x와 같은 군집에 속한 원소들 간의 평균 거리를 의미한다.

• 분리도(Separation)

반대로, 임의의 데이터와 다른 군집에 속해 있는 데이터 간 거리를 구한다. 응집도 개념과 반대로, 군집화가 잘 되어 있을 수록 다른 집단의 데이터와는 더 멀리 떨어져 있을 것이기 때문에, 이 거리는 커져야 한다.

이러한 관점에서 이 거리를 분리도라고 한다. 정확하게 정의하면, 임의의 데이터 x와 다른 군집 중 가장 가까운 군집에 속한 데이터까지의 평균 거리를 의미한다.

이를 바탕으로 다음과 같이 임의의 데이터 x에 대한 실루엣 계수를 정의한다.

\[S_x = \frac {b_x - a_x} {Max(a_x, b_x)} \\ a_x : 응집도, \ b_x : 분리도\]

군집화 품질이 좋지 않아 군집이 겹칠수록 응집도와 분리도 값이 크게 차이가 나지 않을 것이다. 따라서 실루엣 계수가 1에 가까울수록(클수록) 군집화 결과가 좋다고 본다.

3. K-Means++

K-Means 알고리즘의 가장 큰 단점은 군집 초기 중점의 위치를 어떻게 설정하는가에 따라 군집화 품질이 크게 달라질 수 있다는 것이다. 특히 초기 중점이 데이터가 위치한 유클리디안 공간 내에 고루 위치하지 않고, 한 쪽으로 쏠리게 된다면, local optima 문제가 발생한다고 알려져 있다.

이를 위해 초기에 설정하는 중점들이 가능한 한 멀리 혹은 신중하게 선택되도록 중심점 설정의 방식을 변경한 알고리즘이 생겨나게 되었다.

그 중 가장 대표적인 알고리즘이 K-Means++ 알고리즘이다.

위에서 소개한 K-Means 알고리즘에서 2. 과정이 조금 달라진다.

우선, 무작위로 중심점을 선정하는 것이 아니라, 가지고 있는 데이터 중 무작위로 1개를 선정하여 그 지점을 첫 번째 중심점으로 지정한다.

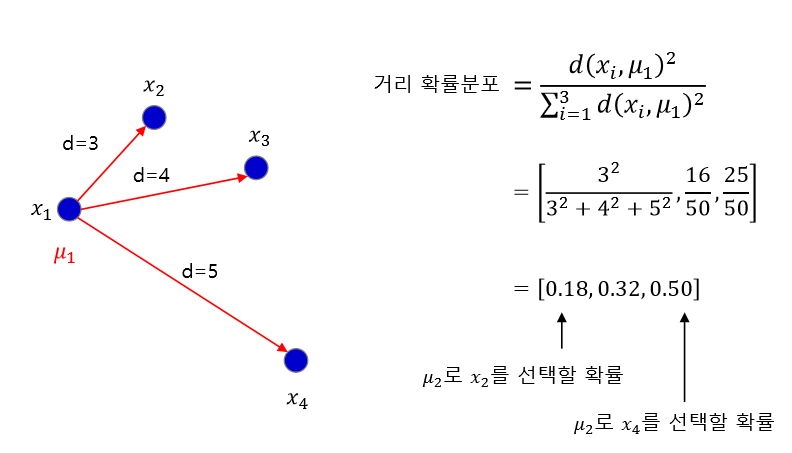
그리고 나머지 데이터들에 대해 첫 번째 중심점으로 지정된 점과의 거리를 계산한다. 그렇게 계산한 거리를 기반으로, 거리 비례 확률에 따라 최대한 멀리 떨어진 데이터 포인트를 다음 중심점으로 선정한다. 중심점이 K개가 될 때까지 위의 과정을 반복하여 초기 중점을 선정한다.

이전 점들과 멀리 떨어진 점들을 선택하다 보면, 자연스럽게 서로 멀리 떨어져 있는 점들이 선택될 것이라는 게 K-Means++ 알고리즘의 아이디어입니다.

_출처: LOVIT x DATA SCIENCE

이 방법을 사용하면 전통적인 K-Means 방법보다 군집화 품질이 더 좋아지며, 수렴 속도가 빨라진다고 알려져 있다.

4. 더 생각해 볼 점

• 기계와 사람의 패턴 인식 차이
• Hybrid Learning(= 주가 패턴 Clustering, 패턴 별 Supervised Learning)을 통한 주가 예측 아이디어
• DBSCAN 알고리즘과의 차이
• MNIST 분류 문제 군집화 성능 향상 방안