[ML] KMeans_2.구현
출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo 1, Github Repo 2
Tensorflow : 2.2.0
K-Means: 코드로 구현하기
1. Scikit-learn
사이킷런으로 K-Means 알고리즘을 구현하는 것은 간단하다. sklearn.cluster에서 KMeans 클래스를 사용하면 된다. 다만, 이전의 이론과 연결하여 parameter를 어떻게 설정해야 하는지, 어떤 메소드를 사용할 수 있는지 기억하는 차원에서 기록하고 넘어가도록 한다.
1.1. parameters
n_clusters: 설정할 군집의 개수(K).init: 초기 중점 설정 방식.random은 전통적인 방식으로 무작위 중심점을 잡는 것이고,k-means++는K-Means++알고리즘을 적용하여 중심점을 설정하는 방식이다. default setting이k-means++이므로, 상당히 편하게 사용할 수 있다.n_init,max_iter: 처음 구현할 때 헷갈렸던 파라미터들이다.n_init: 군집 설정을 위해 몇 번 동안 초기 중심점을 설정할 것인지를 나타낸다.max_iter: 중심점이 수렴하기 까지 몇 번의 중점 업데이트 과정을 거칠 것인지를 나타낸다.
1.2. attributes
cluster_centers_: 중심점의 좌표를 반환한다.labels_: 각 데이터에 부여된 군집의 라벨이다.-
inertia_: 각 데이터에서 중점 좌표까지의 거리 제곱합이다.한편 군집화 결과를 파악하기 위한 실루엣 계수는
sklearn.metrics.silhouette_score클래스를 통해 계산할 수 있다. 사용법은 다음과 같다.
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_samples
km = KMeans(n_clusters=8, init='random', n_init=100, max_iter=300)
km = km.fit(X_data)
y_km = km.predict(X_data)
silhouette_vals = silhouette_samples(X_data, y_km, metric='euclidean')
2. Tensorflow
이제 KMeans 알고리즘을 Tensorflow 코드로 구현해 본다. NumPy 모듈을 이용해 2차원 공간의 데이터를 생성하고, 초기 중심점을 랜덤하게 설정하여 군집화를 수행해 보자.
코드가 좀 어려운 편이다. Tensorflow 사용법과 K-Means 알고리즘의 논리 구현이 어떻게 결합될 수 있는지 확인하는 데에 초점을 맞추자.
참고
강사님의 코드를 함수화하는 과정에서 오류가 있을 수 있다.
2. 1. 모듈 불러오기 및 데이터 준비
# module import
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from matplotlib.pyplot import cm
# create Data
def createData(n):
xy = []
for i in range(n):
if np.random.random() > 0.5:
x = np.random.normal(0.0, 0.9)
y = np.random.normal(0.0, 0.9)
else:
x = np.random.normal(3.0, 0.6)
y = np.random.normal(1.0, 0.6)
xy.append([x, y])
coordinates = np.array(xy, dtype=np.float32)
return coordinates
# 입력 데이터 준비
n = int(input('생성할 좌표의 개수를 설정하세요.: '))
input_data = tf.constant(createData(n))
print(f"입력 데이터(좌표) 형태: {input_data.shape}")
사이킷런의 make_blobs 함수처럼 2차원 공간 내에 좌표 데이터를 만들어 준다. 군집화될 수 있어야 하기 때문에, np.random.random() 조건을 통해 설정되는 x, y 좌표가 따르는 분포가 달라지도록 했다.
공간 상에 뿌려질 데이터의 좌표는 변하면 안 되기 때문에, tf.constant로 선언한다.
2. 2. 군집화
중첩된 for문을 사용해 군집화 과정을 수행한다.
k: 군집 개수.i: 사이킷런에서n_init역할을 한다. 초기 중점을 몇 번 잡을 것인지 결정한다.j: 사이킷런에서max_iter역할을 한다.i의 내부 반복문으로서 중점 업데이트를 몇 번까지 수행할 것인지 결정한다.c: 중점을 업데이트한다.
에러는 각 데이터와 군집 중점까지의 거리 제곱합으로 정의한다.
def kmeans_tf(k, n_init, max_iter, data=input_data, tol=0.0001):
'''
k: 초기 중점의 개수
n_init: 초기 중점 설정 횟수
max_iter: 중점 업데이트 횟수
data: 군집화할 데이터
tol: 최소 에러 감소폭(수렴 판단 위해)
'''
final_error = np.inf # 최종 에러
error_history = [] # 에러 기록
# 1) 중점 설정
for i in range(n_init):
prev_error = 0
# 2) 초기 중점 좌표 설정: 랜덤.
tmp_data = tf.random.shuffle(data)
tmp_cent = tf.slice(tmp_data, [0, 0], [k, -1])
centroid = tf.Variable(tmp_cent)
# 3) 중점 좌표 업데이트
for j in range(max_iter):
exp_data = tf.expand_dims(data, axis=0)
exp_cent = tf.expand_dims(centroid, axis=1)
# 4) 데이터와 중심 좌표 거리 계산
tmp_dist = tf.square(tf.subtract(exp_data, exp_cent))
dist = tf.sqrt(tf.reduce_sum(tmp_dist, axis=2))
error = tf.reduce_sum(dist)
# 5) 중점 할당
assignment = tf.argmin(dist)
# 6) 중점 좌표 계산
for c in range(k):
equal = tf.equal(assignment, c)
where = tf.where(equal)
reshape = tf.reshape(where, [-1])
gather = tf.gather(data, flat)
mean = tf.reduce_mean(gather, axis=0)
# 7) k개의 중점 좌표 모으기
if c == 0: # 0번 라벨 중점
concat_mean = tf.concat(mean, axis=0)
else:
concat_mean = tf.concat([concat_mean, new_mean], axis=0)
# 8) 중점 좌표 2차원 reshape
mean_data = tf.reshape(concat_mean, [k, 2])
# 9) 새로운 중점 업데이트
centroid.assign(mean_data)
# 10) 수렴 조건 설정
if np.abs(error-prev_error) < tol:
break
# 11) 에러 업데이트
prev_error = error
# 12) 기록
if error < final_error:
final_cent = centroid.numpy().copy()
final_cluster = assignment.numpy().copy()
final_error = error
error_history.append(final_error)
print("%d Done" % i)
return final_cent, final_cluster, final_error, error_history
1), 2) 초기 중점 좌표 할당
초기 중점의 좌표를 100번 동안 설정한다.
K-Means++ 알고리즘과 random 방식의 미묘한(?) 조화다. 데이터를 섞은 후, 앞의 k개를 초기 중점으로 설정한다. 이렇게 설정된 초기 중점의 좌표는 계속해서 변할 것이므로, tf.Variable을 활용해 변수로 선언한다.
초기 중점으로 설정하는 과정에서 tf.slice 함수가 사용되었다. 공식 문서와 문서에 등장하는 예제를 통해 확인한 바로는, 각 차원의 위치(첫 번째 인자)에서 두 번째 인자 만큼의 요소를 뽑아내는 함수인 것 같다. -1을 사용할 경우 모든 요소를 다 추출한다.
tf.random.shuffle을 통해 데이터를 섞은 뒤, 앞의 k개를 중점의 좌표로 설정한다.
3), 4) 중점 좌표 할당
중점 좌표를 설정하기 위해 행렬의 차원을 확장하여 계산했다. 3차원 텐서로 차원을 확장하여 계산하는데, 이 과정을 정확하게 수학적으로 이해하는 것은 그 범위를 넘는다고 생각해 다음의 강의 자료로 설명을 대체한다.
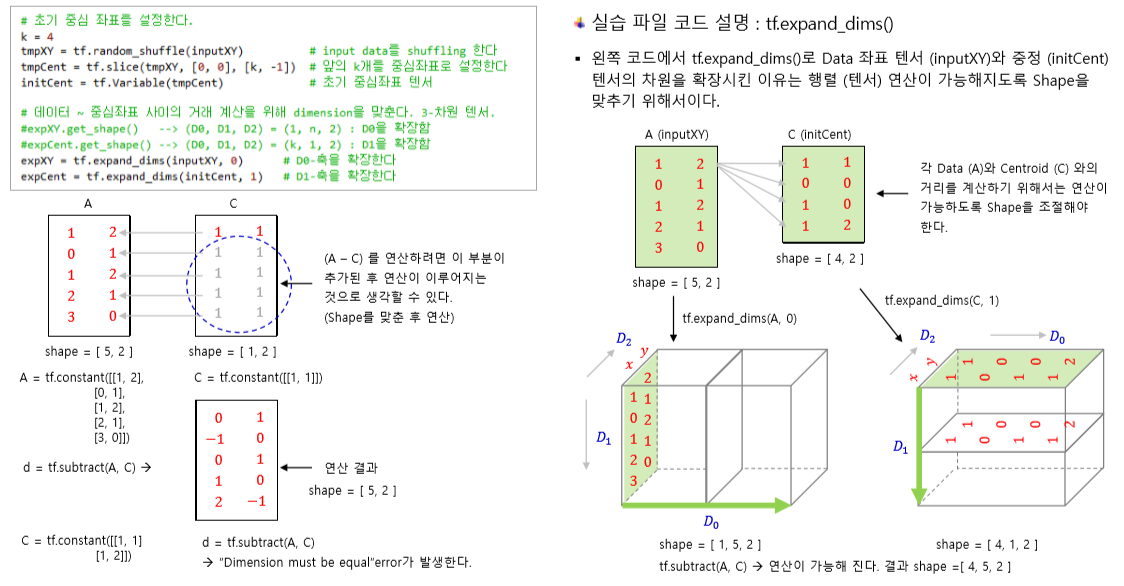
거리 계산은 KNN 알고리즘을 구현하는 로직에서와 동일하게 tf.reduce_sum을 이용한다. 처음 거리 계산을 위해 3차원 텐서로 확장했기 때문에, D2축으로 합치고, 거리의 총합을 계산하기 위해 axis=0 방향으로 합쳐 거리 제곱합을 계산한다.
계산한 에러(error)는 다음과 같은 형태를 갖는데, 사이킷런에서의 inertia_와 동일하다.
tf.Tensor(12909.11937, shape=(), dtype=float32)
5) 중점 할당
위의 과정까지 진행하면 다음과 같이 중점과의 거리가 나오게 된다.
tf.Tensor(
[[5.327714 2.0052502 0. 4.4746113 4.3265786 1.4065863
0.6989805 1.3353246 4.814999 3.8987234 ]
[2.049295 2.368372 4.3265786 1.3150858 0. 3.565032
3.729206 3.0226884 1.6295482 0.66886806]
...
[5.0345163 1.2913861 1.4065863 4.1100655 3.565032 0.
1.4319366 1.35906 4.4964886 3.3272238 ]
[0. 3.7438343 5.327714 0.9313209 2.049295 5.0345163
4.6352916 4.025502 0.5382489 1.8239815 ]], shape=(1000, 10), dtype=float32)
각각에 대해 tf.argmin 함수를 사용해 어떤 중점과의 좌표 거리가 가장 짧은지 계산한다. 그 결과 나온 index가 가장 거리가 짧은 좌표 거리다.
tf.Tensor([4 3 0 2 1 ... 3 0 0 2 1], shape=(1000,), dtype=int64)
6) 중점 평균 좌표 계산
이제 각 중점별로 좌표를 모아서 평균 좌표를 계산한다. tf.equal을 통해 assign된 클러스터 라벨을 확인하고, tf.where과 tf.gather를 이용해 해당 클러스터 라벨에 해당하는 좌표들을 모두 모은다.
모으는 과정에서 tf.reshape을 활용했는데, 별 건 아니다.
# 클러스터 라벨 c = 0인 좌표들을 구하는 과정
# tf.equal 수행 결과
[ True False False False False True True True False False ... ]
# tf.where 수행 결과
[[0] [5] [6] [7]]
tf.where을 수행하고 나면, True가 몇 번째 있는지 그 위치를 반환하게 된다. 그런데 그 결과가 위와 같이 2차원 Tensor이기 때문에, 이를 flatten한 후, 해당 Tensor를 인덱스로 삼아 좌표들을 모아오기 위함이다.
tf.gather를 이용해 각 좌표들을 모아 오고, tf.reduce_mean을 이용해 axis=0 방향으로 평균 거리를 계산해 준다.
7), 8), 9) 중점 좌표 업데이트
이렇게 모인 계산한 평균 좌표들을 모아 2차원 좌표 형태로 reshape한다. 클러스터 라벨이 0일 때의 평균 좌표를 초기값으로 삼고, 이후의 중점 좌표를 tf.concat을 통해 쌓아준 뒤, (k, 2) 형태의 2차원 Tensor로 만들어 준다.
이제 assign을 이용해 이 Tensor를 새로운 중점 좌표로 설정하면 된다.
10) 수렴 조건 설정
EM 알고리즘의 원리에 의해 중점 좌표가 수렴하면(변경되지 않는다면) 업데이트 과정을 중지한다고 했다.
이를 구현하기 위해 error를 활용했다. 에러 변화 폭이 매우 미미하다면(tol 인자로 구현한다.) 중점의 이동폭이 크지 않아 에러 변화가 크지 않았다는 것으로 판단하여 업데이트를 중지하고 반복문 순회를 중지한다.
2. 3. 결과 확인
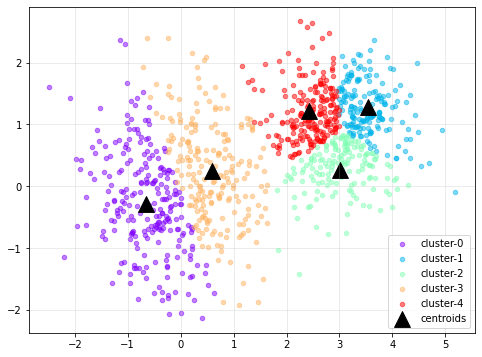
1000개의 데이터에 대해 클러스터의 개수를 5, 초기 중점 설정 횟수를 100, 중점 업데이트 limit을 200으로 하여 K-Means 알고리즘을 Tensorflow로 구현한 결과는 다음과 같다.
| 군집화 결과 | SSE |
|---|---|
 |
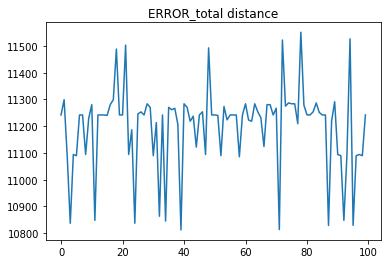 |
데이터 형태를 눈으로만 본다면 군집의 개수가 이보다 적었어야 할 것 같다. 왼쪽 1개, 오른쪽 1개로 2개 정도의 군집을 설정하는 게 더 적당했을 수도 있다.
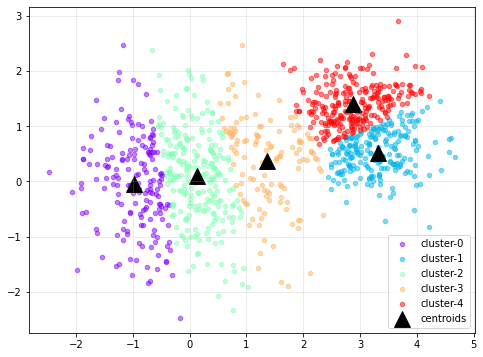
혹시 몰라 한 번 더 수행해 본 결과는 다음과 같다. 역시나(;;) 별로 좋아 보이지는 않는다.
| 군집화 결과 | SSE |
|---|---|
 |
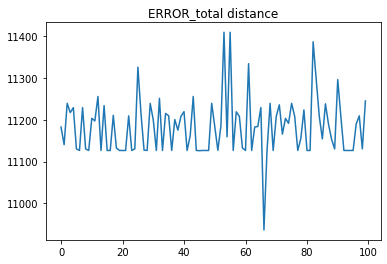 |
Elbow Method를 통해 적당한 군집의 개수를 찾아 보려고 했다. 군집의 개수를 2부터 31사이로 설정해 각 군집 개수 별로 최소 SSE를 기록하고 이를 시각화했다.

음. 뭔가 코드가 이상한 듯하다… elbow는 커녕 직선으로 쭉 올라간다니… 뭐죠? 일단 너무 졸리니까 다음에 다시 확인해 보는 걸로 합시다
결과 확인을 위해 작성한 모든 코드는 다음과 같다.
3.1. k = 5일 때
k = int(input('초기 중점 좌표의 개수를 설정하세요.: '))
n = int(input('초기 중점 설정 횟수를 설정하세요.: '))
iteration = int(input('중점 업데이트 횟수를 설정하세요.: '))
centroid, cluster, error, history = kmeans_tf(k, n, iteration, data=input_data, tol=0.0001)
data = input_data.numpy()
# 군집 시각화
color = cm.rainbow(np.linspace(0, 1, k))
plt.figure(figsize=(8, 6))
for i, c in zip(range(k), color): # 모든 데이터
plt.scatter(data[cluster==i, 0], data[cluster==i, 1],
s=20, color=c, marker='o', alpha=0.5,
label=f'cluster-{i}')
plt.scatter(centroid[:, 0], centroid[:, 1], # 중점
s=250, marker='^', color='black',
label='centroids')
plt.legend()
plt.gird(alpha=0.3)
plt.show()
# SSE 시각화
plt.plot(history)
plt.title('ERROR_total distance')
plt.show()
3.2. k 조정
min_error_history = []
for c_num in range(2, 101):
_, _, error, _ = kmeans_tf(c_num, 100, 200)
min_error_history.append(error)
# 시각화
plt.plot(min_error_history)
뭔가 코드가 이상한 것 같은데, 어디서 이상한지 모르겠다.


댓글남기기