[ML] KNN_2.구현
출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo
Tensorflow : 2.2.0
KNN: 코드로 구현하기
이제 KNN 알고리즘을 머신러닝 코드로 구현해 보자. Scikit-learn으로 구현하면 간단하지만, Tensorflow로는 살짝 복잡해 진다.
대출 신용 평가 데이터를 이용하여 이진 분류(클래스: 0, 1) 작업을 수행한다.
1. 모듈 불러오기 및 데이터 준비
# module import
import pandas as pd
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
# load data
data = pd.read_csv('./dataset/3-4.credit_data.csv')
data = np.array(data)
데이터를 불러온 뒤 2차원 NumPy 배열 형태로 만들어 준다.
2. 데이터 분리
훈련용과 시험용으로 데이터를 분리한다. 훈련용 데이터로 80%를 사용한다. 분리한 뒤, 라벨에 해당하는 데이터를 2차원 배열로 reshape한다.
# split data: train_size 0.8
train_num = int(len(data) * 0.8)
X_train, X_test = data[:train_num, :-1], data[train_num:, :-1]
y_train, y_test = data[:train_num, -1], data[train_num:, -1]
# reshape labels
y_train = y_train.reshape(len(y_train), 1)
y_test = y_test.reshape(len(y_test), 1)
각 데이터는 6개의 feature를 가진 6차원 공간 상의 데이터이다.
앞에서도 말했듯, KNN 알고리즘에서 훈련 데이터는 ‘학습’이 아니라, 테스트 데이터와의 거리를 계산하기 위한 데이터라는 점에 주의하자.
3. KNN 분류
3.1. 기본 원리
6차원 유클리디안 공간에 399개의 훈련용 데이터와 100개의 시험용 데이터가 위치해 있다. 100개의 시험용 데이터 각각에 대해, 399개의 훈련용 데이터와의 유클리디안 거리를 계산한다. 그리고 지정한 이웃의 수(K)를 기준으로 가장 짧은 거리를 갖는 훈련용 데이터들을 골라 낸다.
이렇게 선정한 가장 가까운 이웃들의 클래스를 확인한다. 더 많은 클래스를 시험용 데이터와의 클래스로 결정한다.
먼저 연습 삼아 K=5로 삼아 5개의 최근접 이웃을 바탕으로 100개 시험용 데이터의 클래스를 예측해 본다.
3.2. 거리 측정
x가 임의의 훈련 데이터라고 하자.
x = x.reshape(1, 6)
distance = tf.sqrt(tf.reduce_sum(tf.math.square(tf.subtract(X_train, x)), axis=1))
각각의 테스트 데이터는 (6, ) 형태의 1차원 배열이다. 훈련 데이터 각각이 (399, 6) 형태의 2차원 배열로 되어 있기 때문에, 테스트 데이터를 (1, 6) 형태로 reshape한다. reshape한 후, 거리를 계산하는 연산을 수행하면 내부적으로 broadcasting이 수행되어 훈련 데이터 각각에 대해 하나의 테스트 데이터와 거리를 계산할 수 있게 된다.
유클리디안 거리 계산 공식에 따라 거리를 측정한다. 식을 써줘도 되지만, Tensorflow 내부에서 더 연산이 잘 수행되도록 하기 위해 tf.subtract, tf.math.square 등의 함수를 사용했다.
거리 계산 시 주의해주어야 하는 부분은 tf.reduce_sum이다. Tensorflow 공식 문서에 따르면, reduce_sum 연산을 수행할 때 axis 방향을 어떻게 설정하는가에 따라 연산 결과가 달라진다.
참고
x = tf.constant([[1, 1, 1], [1, 1, 1]]) tf.reduce_sum(x) # 6 tf.reduce_sum(x, 0) # [2, 2, 2] tf.reduce_sum(x, 1) # [3, 3] tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]] tf.reduce_sum(x, [0, 1]) # 6
거리를 계산한 뒤 텐서 형태는 다음과 같은 (399, 6) 형태의 Tensor이다.
tf.Tensor(
[[-1.040e-01 1.850e-01 8.720e-01 1.233e+00 -1.150e-01 0.000e+00]
[ 1.442e+00 1.350e-01 0.000e+00 0.000e+00 3.910e-01 0.000e+00]
...
[-2.920e-01 3.400e-02 4.240e-01 2.060e-01 -5.740e-01 0.000e+00]], shape=(399, 6), dtype=float64)
행 방향으로의 차원을 유지하면서 열 방향으로 더해줘야 399개 훈련 데이터 각각에 대한 테스트 데이터의 거리를 계산할 수 있게 되므로, axis=1 방향의 차원을 제거해 준다.
3.3. 최근접 이웃 선정
values, indices = tf.math.top_k(tf.negative(distance), k=5, sorted=False)
3-2 단계까지 수행하면 각 테스트 데이터 하나에 대해 399개의 훈련 데이터 모두와 유클리디안 거리를 계산한 (399, ) 형태의 Tensor가 나오게 된다.
tf.Tensor(
[2.33893900e+00 2.25047000e+00 1.67783400e+00 9.71729200e+00 ... 1.10191200e+00 4.52276300e+00 6.38108000e-01], shape=(399,), dtype=float64)
여기서 거리가 가장 짧은 5개의 데이터를 골라 내야 한다. 이를 위해 tf.math.top_k 함수를 활용한다. (tf.nn.top_k 함수를 활용해도 된다.) 텐서 내에 가장 값이 큰 k개의 데이터를 선정해 값과 인덱스를 반환하는 함수다. KNN 알고리즘을 적용할 때는 거리가 가장 짧은 데이터를 골라야 하므로, 위의 단계에서 구한 거리를 음수로 만들어 주고 5개를 고르면 된다.
참고 :
sorted=False
sorted=True옵션을 주면, 데이터를 오름차순 혹은 내림차순(ascending옵션으로 설정한다)으로 정렬한 뒤 인덱스를 반환한다. 그러나 이후 단계에서 훈련 데이터의 index를 활용해 최근접 이웃을 골라 내야 하므로,sorted된 상태에서 인덱스를 반환하면 안 된다.
3.4. 클래스 판단
classMean = tf.reduce_mean(tf.cast(tf.gather(y_train, indices), dtype=tf.float32))
tf.gather 함수를 이용해 3.3.에서 고른 최근접 이웃의 인덱스에 해당하는 라벨을 가져 온다. 라벨이 0, 1 중 하나이므로, 라벨들의 평균을 내면 0과 1 사이의 수치를 구할 수 있다.
이 수치가 0.5를 기준으로 크다면 그 클래스가 1인 것으로, 아니라면 0인 것으로 판단한다. 1인 라벨이 더 많다면 그 평균 라벨의 수치가 0.5보다 클 것이기 때문에 매우 직관적인 접근이다.
3.5. 모든 테스트 데이터에 대해 작업 진행
이제 모든 테스트 데이터에 대해 위의 작업을 진행한다. 예측치를 구하는 부분이 2차원 배열 형태로 달라지고, 정확도를 구하는 부분이 추가된다.
y_hat = [] # 각각의 테스트 데이터에 대해 class 평균 수치를 기록할 배열
for x in X_test:
x = x.reshape(1, 6)
distance = tf.sqrt(tf.reduce_sum(tf.math.square(tf.subtract(X_train, x)), axis=1))
values, indices = tf.math.top_k(tf.negative(distance), k=5, sorted=False)
classMean = tf.reduce_mean(tf.cast(tf.gather(y_train, indices), dtype=tf.float32))
y_hat.append(classMean.numpy()) # class 평균 수치 기록
y_hat = np.array(y_hat)
y_hat = y_hat.reshape(len(y_hat), 1) # 2차원 배열로 변형
y_hat_pred = np.wehre(y_hat > 0.5, 1, 0)
# 정확도
accuracy = (y_test == y_hat_pred).sum() / len(y_test)
3.6. 최적의 k 찾기
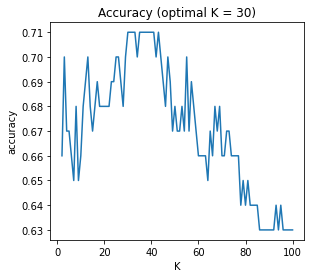
이제 K의 범위를 설정한 뒤(min_K ~ max_K), 최적의 정확도를 보인 K를 찾으면 30이 된다.
| 최적 K | 최적일 때 추정치 분포 |
|---|---|
 |
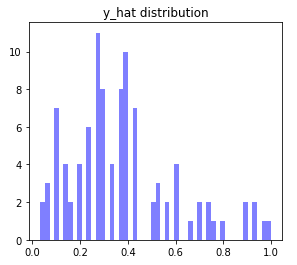 |
K = 30으로 설정할 때 최적의 정확도가 나온다. 다만, 이 때 클래스 추정 점수의 분포를 보면 그다지 마음에 들지는 않는다. 양쪽으로 퍼질수록 더 확실하게 분류된 것인데, 그렇지는 않아 보인다.
전체 코드는 다음과 같다. (정확도 측정 부분을 이전에 문쌤에게 배웠던 방식으로 바꿔서 진행해 봤다. 결과는 동일하다.)
accuracy_history = [] # 정확도 변화 기록
opt_K, opt_acc = 0, 0.0 # 최적의 정확도를 기록한 K와 정확도 수치
min_K, max_K = 2, 100 # 검사할 K의 범위
y_hat_opt = [] # 최적 K에서의 y 검사 추정치
for k in range(min_K, max_K+1):
y_hat = []
for x in X_test:
x = x.reshape(1, 6)
distance = tf.sqrt(tf.reduce_sum(tf.math.square(tf.subtract(X_train, x)), axis=1))
values, indies = tf.math.top_k(tf.negative(distance), k=k, sorted=False)
classMean = tf.reduce_mean(tf.cast(tf.gather(y_train, indices), dtype=tf.float32))
y_hat.append(classMean.numpy())
y_hat = np.array(y_hat)
y_hat = y_hat.reshape(len(y_hat), 1)
y_hat_pred = np.where(y_hat > 0.5, 1, 0)
accuracy = tf.reduce_mean(tf.cast(tf.equal(y_test, y_hat_pred), dtype=tf.float32))
# 최고 정확도 기록했을 때 클래스 추정 점수, k, 정확도 기록.
if accuracy > opt_acc:
y_hat_opt = y_hat.copy()
opt_K = k
opt_acc = accuracy
# history 기록
accuracy_history.append(accuracy)
print("k = %d, DONE!" %k)
# plot
fig = plt.figure(figsize=(10, 4))
p1, p2 = fig.add.subplot(1,2,1), fig.add_subplot(1,2,2)
X_range = np.arange(min_K, max_K+1)
# 정확도
p1.plot(X_range, accuracy_history)
p1.set_title('Accuracy (optimal K = ' + str(opt_K) + ')')
p1.set_xlabel('K')
p1.set_ylabel('accuracy')
# 추정치 분포
n, bins, patches = p2.hist(y_hat_opt, 50, facecolor='blue', alpha=0.5)
plt.show()
4. 기타
-
KNN 알고리즘을 구현하는 과정에서는 이렇다 할 학습 과정이 없음에 다시 한 번 주의하자. loss function도 정의하지 않는다.
-
지금 예시에서는 binary classification이기 때문에, 0과 1의 클래스만 있었고, 지정한 수의 최근접 이웃들이 가진 클래스의 평균 점수를 기반으로 class를 예측하는 것이 가능했다. 그런데 만약 multinomial classification이라면 점수를 어떻게 내야 할까? 이진 분류를 여러 번 수행하는 방식으로 점수를 여러 번 매겨야 할까..?


댓글남기기