[AI] Matrix Factorization Techniques for Recommender Systems 리뷰

^{논문( 출처 ): Matrix Factorization Techniques for Recommender Systems} 

2006년 Netflix Prize 이후로 추천시스템 분야에서 전례 없던 대량의 데이터가 공개되며 추천시스템, 특히 Collaborative Filtering 분야가 크게 발달했다. 그리고 해당 대회에 참여해 Matrix Factorization 기법을 사용해 좋은 성적을 거둔 BellKor 팀에서 추천시스템 및 Matrix Factorization 기법에 대해 리뷰한 논문을 발표했다.

Matrix Factorization 기법에 대한 설명이 잘 되어 있다 (그래서 대회 우승했겠지만). 논문의 대략적 구성은 다음과 같다.

• Introduction: 추천시스템의 필요성 및 발전
• Recommender System Strategies: 추천시스템 기법 전반에 대한 소개
• Matrix Factorization: Matrix Factorization 기법에 대한 (상세한) 소개
• Netflix Prize Competition: 해당 대회에서 중점을 둔 부분, 결과

전반적으로 Matrix Factorization 기법, 특히 기본적인 모델에서부터 다양한 요인들을 어떻게 고려해 나가며 모델을 설계하는지를 설명한 논문인 만큼, 이에 중점을 두어 리뷰하고자 한다.

1. 추천시스템

시장에 너무 많은 상품이 있고, 그에 따라 선택의 폭이 넓어지며 소비자들을 적절한 상품과 매칭하는 것이 중요한 일이 되었다. 이를 통해 소비자들의 만족과 충성도를 높이고, 소비자 경험의 폭을 넓힐 수 있기 때문이다. 이러한 맥락에서 사용자의 상품에 대한 흥미와 관심을 분석하여, 해당 사용자(의 입맛 혹은 기호)에 맞는 개인화된 추천을 제공하는 추천시스템이 발전해 왔다.

추천시스템^{이 맥락에서는 apriori 알고리즘 등 rule 기반의 추천시스템 이후의 것을 말하는 듯하다}  에는 크게 상품이나 사용자에 대한 정보를 기반으로 하는 1) Contents Filterting과 사용자의 과거 행동을 바탕으로 사용자와 상품 간 관계를 찾고자 하는 2) Collaborative Filtering의 두 가지 접근법이 있다.

Broadly Speaking, recommender systems are based on one of two strategies. The content filtering approach creates a profile for each user or product to characterize its nature. (…) An alternative to content filtering relies only on past user behavior—for example, previous transactions or product ratings— without requiring the creation of explicit profiles. This approach is known as collaborative filtering, (…)

Contents Filtering

각각의 사용자나 아이템의 본질을 설명하는 프로필을 만들어, 그 내용을 바탕으로 비슷한 것을 추천한다. 해당 프로필을 만들 때 활용할 수 있는 정보로는 다음의 것들이 있다. 물론 아래의 것들과 달리 명시적으로 관련 있어 보이지 않는 외부 정보를 활용해도 된다.

• 사용자: 성별, 나이 등의 demographic information, 설문지 답변 등
• 아이템: (영화를 예로 들면) 장르, 출연 배우, 박스오피스 순위 등

대표적인 예로 음악 전문가들이 모여 수많은 음악을 분류하고자 했던 Music Genome Project가 있다. 당연히 정보를 모으고 분류하는 데에 시간이 많이 든다.

Collaborative Filtering

구매, 구매 후 평가 등 사용자의 과거 행동에 대한 데이터만을 기반으로 사용자와 상품에 존재하는 관련성을 찾아내어(조금 더 엄밀히 말하면 컴퓨터가 찾아내도록 하여) 추천한다. Contents Filtering에 비해 다음의 장단점이 있다.

• 장점
  • domain-free: profile 정보를 만들 필요가 없으므로 domain 지식 불필요
  • address elusive data: contents filtering에서는 사용할 수 없는 로그, 구매 이력 등 사용자 행동 데이터 활용 가능
• 단점: cold start problem

관련성을 찾아내기 위해 사용하기 위한 전략으로 1) Neighborhood Methods와 2) Latent Factor Models가 있다.

Neighborhood Methods

이 방법에서의 관련성은 사용자 간 혹은 아이템 간 유사성을 계산한다. 비슷한 유저들을 찾아 내는 user-based approach와, 비슷한 아이템을 찾아내는 item-based approach가 있다. 어떤 사용자를 혹은 아이템을 비슷하다고 볼 것인지의 맥락에서, 유사성을 계산하는 방법이 중요하다.

Latent Factor Models

이 방법에서의 관련성은 사용자와 상품 간의 관련성이다. 이를 위해 사용자의 평가 패턴 데이터^{어떻게 보면 평가 외에 구매 여부 등도 될 수 있을 것이라 보인다} 로부터 내재된 요인(latent factors)을 찾아내고자 한다.

논문에서는 이 방법이 어떻게 보면 Contents Filtering에서 사람이 직접 요인별로 만들었던 프로필을 컴퓨터가 알아서 찾게 하는 것이라고도 한다.

In a sense, such factors comprise a computerized alternative to the aforemetioned human-created song genres.

다만, 이 요인들을 어떻게 해석해야 하는지의 문제가 남는다. 어떤 측면에서 본다면, 그 요인들을 해석하지 못하니까 사람이 못 찾아내는 latent factor이지 않을까 싶기도 하다.

내재된 요인의 수를 $d$라고 할 때, 사용자와 아이템을 모두 $d$차원의 내재 공간(latent space)으로 매핑한 후, 사용자와 아이템이 얼마나 관련되었는지 벡터 내적을 통해 계산한다.

2. Matrix Factorization

위에서 설명한 Collaborative Filtering의 Latent Factor Model 중 가장 성공적인 방법은 Matrix Factorization를 사용한 방법이다. 즉, 잠재요인을 찾아내고 해당 공간으로 사용자와 아이템을 매핑하기 위해 Matrix Factorization 기법을 이용한다. 이 기법은 검색 기록, 구매 이력, 검색 패턴, 마우스 이동 등 implicit feedback도 활용하여 사용자의 선호를 파악할 수 있게 해 주고, 그럼으로써 sparsity가 문제가 되는 user-item matrix를 densely filled matrix로 만들어준다(=ratings 예측).

Basic Matrix Factorization Model

Matrix Factorization은 사용자의 아이템 평가 패턴으로부터 사용자와 아이템을 동일한 factor들로 이루어진 벡터로 표현한다. 사용자 벡터와 아이템 벡터의 연관성이 높아질수록 추천받을 확률이 높아진다.

^{위와 같은 상태에서 3번 사용자는 5번 아이템과의 연관성이 높고, 이에 따라 5번 아이템을 추천받을 확률이 높아진다.}

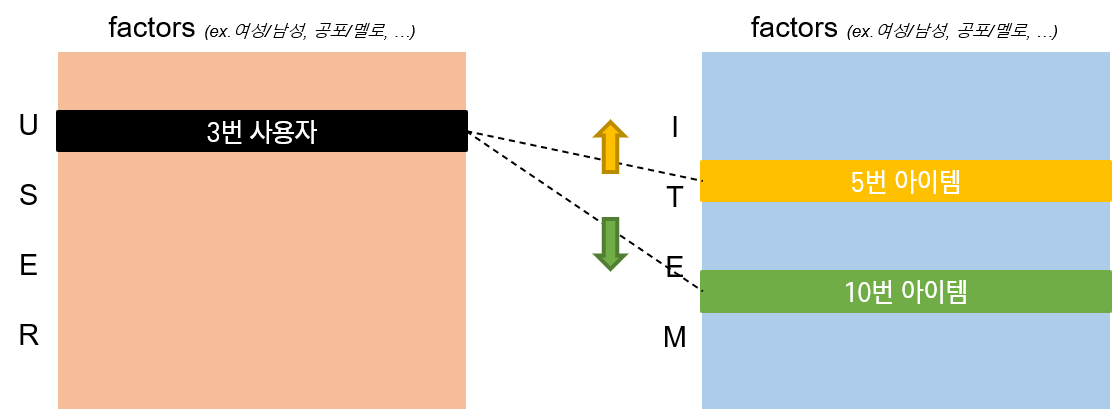
따라서 기본적으로 Matrix Factorization 모델은 모든 사용자와 아이템을 f 차원의 공통의 latent space로 매핑한다. 그러면 아이템 $i$의 벡터 \(q_i \in \mathbb{R}^f\), 사용자 $u$의 벡터 \(p_u \in \mathbb{R}^f\)는 각각 해당 아이템이 $f$ 개의 요인들 각각을 얼마나 가지고 있는지, 해당 사용자가 상응하는 요인들을 갖는 아이템에 얼마나 관심을 가지고 있는지를 나타낸다. 이 때, 두 벡터의 내적 \(q_i^T \cdot p_u\)는 유저 $u$가 아이템 $i$에 얼마나 관심을 가지고 있는지(이하 interaction)를 의미한다. 이 interaction은 사용자 $u$의 아이템 $i$에 대한 평가일 것이다(논문에서는 approximates라는 표현을 사용했다).

\[\hat {r}_{ui} = q_i^T \cdot p_u\]

결과적으로 이 모델을 사용할 때 있어 가장 중요한 것은 latent space로의 mapping function을 찾아, 각 사용자와 아이템을 \(q_i, p_u \in \mathbb{R}^f\)로 매핑하는 것이다.

따라서 Matrix Factorization은 위와 같은 매핑 문제를 풀기 위해 있는(=관측된) 평가 데이터를 학습하여, 없는 (=관측되지 않은, 혹은 미래의) 평가 데이터를 예측한다. 이 때, 있는 데이터 자체가 적기 때문에, 기존의 데이터에 과적합되는 것을 막기 위해 regularization 항을 둔다. 따라서 loss function은 학습 데이터(=user-item matrix에서 값이 있는, 알려진 부분)에 대한 regularized squared error이다.

\(\ \min_{p*, q*} \Sigma_{(u, i)\in \kappa} (r_{ui}-q_i^Tp_u)^2 + \lambda(||q_i||^2 + ||p_u||^2)\)

참고: Matrix Factorization의 SVD

SVD를 사용할 수 없을까 생각했는데, 안 그래도 논문에 다음과 같은 내용이 있다.

Such a model is closely related to singular value decomposition( SVD), a well-established technique for identifying latent semantic factors in information retrieval. Applying SVD in the collaborative filtering domain requires factoring the user-item rating matrix. This often raises difficulties due to the high portion of missing values caused by sparseness in the user-item ratings matrix. Conventional SVD is undefined when knowledge about the matrix is incomplete. (…)

Earlier systems relied on imputation to fill in missing ratings and make the rating matrix dense. (…)

이에 따라, SVD^{라고는 하지만 기존 선형대수학 기반 행렬분해 이론을 모두 적용할 수 없을 듯하다. 전부 imputation의 문제가 있지 않을까?} 보다는, 학습 및 예측을 통해 user-item matrix를 factorizing하는 것이 추천시스템에서의 정석적인 Matrix Factorization인 듯하다. 이걸 FunkSVD라고도 하는 것 같은데, 팩트 체크 필요!

학습 알고리즘

위와 같은 Matrix Factorization을 수행하기 위한 알고리즘으로 다음의 두 가지가 있다.

SGD(Stochastic Gradient Descent)

한 번 학습할 때 training set에 있는 모든 rating을 순회하면서 예측 오차를 계산하고, 가중치를 업데이트한다. 이 때 예측 오차는 다음과 같이 정의된다.

\[e_{ui} = r_{ui} - q_i^T \cdot p_u\]

학습률을 \(\gamma\)라고 할 때, 계산된 예측오차에 기반하여 그래디언트의 반대 방향으로 다음과 같이 각 파라미터를 업데이트한다.

\[q_i \leftarrow q_i + \gamma \cdot(e_{ui}\cdot p_u - \gamma \cdot q_i) \\ p_u \leftarrow p_u + \gamma \cdot(e_{ui}\cdot q_i - \gamma \cdot p_u)\]

ALS(Alternating Least Squares)

\(p_u\)와 \(q_i\) 중 하나를 고정한다면, Matrix Factorization이 풀어야 할 문제는 quadratic optimization 문제가 된다. 따라서 ALS 알고리즘은 \(p_u\)와 \(q_i\) 중 하나를 고정한 후, 나머지 한 변수에 대한 least squares 문제를 풀어 최적화한 뒤, 다른 변수에 대해 최적화하는 과정을 반복해 나간다.

SGD보다 더 느리게 수렴하지만, 그럼에도 불구하고 다음의 두 가지 경우에는 ALS 방법이 좋은 것으로 알려져 있다.

• parallelization이 가능할 때
• implicit data의 활용이 중요할 때

모델의 고도화

이후 Basic Matrix Factorization에 사용되는 모델을 어떻게 구체화하며 다른 변수들을 고려할 수 있을지에 대한 내용이 나온다. (사실 모든 내용이 다 하나의 소제목으로 다뤄지지만, 공통적으로 기본 모델에 어떻게 다른 데이터를 결합할 수 있을지의 이야기라는 측면에서 하나의 내용으로 간주하고 작성한다)

Adding Bias

rating에 사용자와 아이템 각각에 bias가 있을 수 있다고 보고, rating을 순수한 interaction과 bias 부분으로 나눈다. 이 때, 사용자의 rating에 대한 예측값은 다음과 같이 정의할 수 있다.

\[\hat {r_{ui}} = \mu + b_i + b_u + q_i^T \cdot p_u\]

• \(\mu\) : rating 평균
• \(b_i\) : item bias, 예컨대, 특정 영화가 전반적으로 낮은 평점을 받는 경우
• \(b_u\) : user bias, 예컨대, 모든 영화에 대해 다 낮은 평점을 주는 사용자
• \(q_i^T \cdot p_u\) : 사용자와 아이템 간 상호작용

이 때 Matrix Factorization 모델이 최소화해야 할 MSE 에러는 다음과 같아진다.

\(\ \min_{p*, q*, b*} \Sigma_{(u, i)\in \kappa} (r_{ui}-\mu - b_i - b_u - q_i^T \cdot p_u)^2 + \lambda(||q_i||^2 + ||p_u||^2+{b_u}^2 +{b_i}^2)\)

Additional Input Sources

rating 데이터가 적을 때 다른 데이터를 활용하여 모델을 구성할 수도 있다. 이 측면을 잘 활용하면 cold start problem을 해결할 수 있다.

예컨대,