[NLP] TF-IDF
조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. Github Repo
Tensorflow : 2.2.0
TF-IDF
1. 개요
여러 개의 문서(= 문장)가 있을 때, 각각의 문서 내에 있는 단어에 수치적 중요도를 부여하여 단어를 수치화하는 방법이다. 빈도 (count)를 기반으로 단어에 중요도를 부여하고, 그것을 수치로 나타낸다.
TF-IDF를 엑셀로 구현해 놓은 교재 파일을 보자.
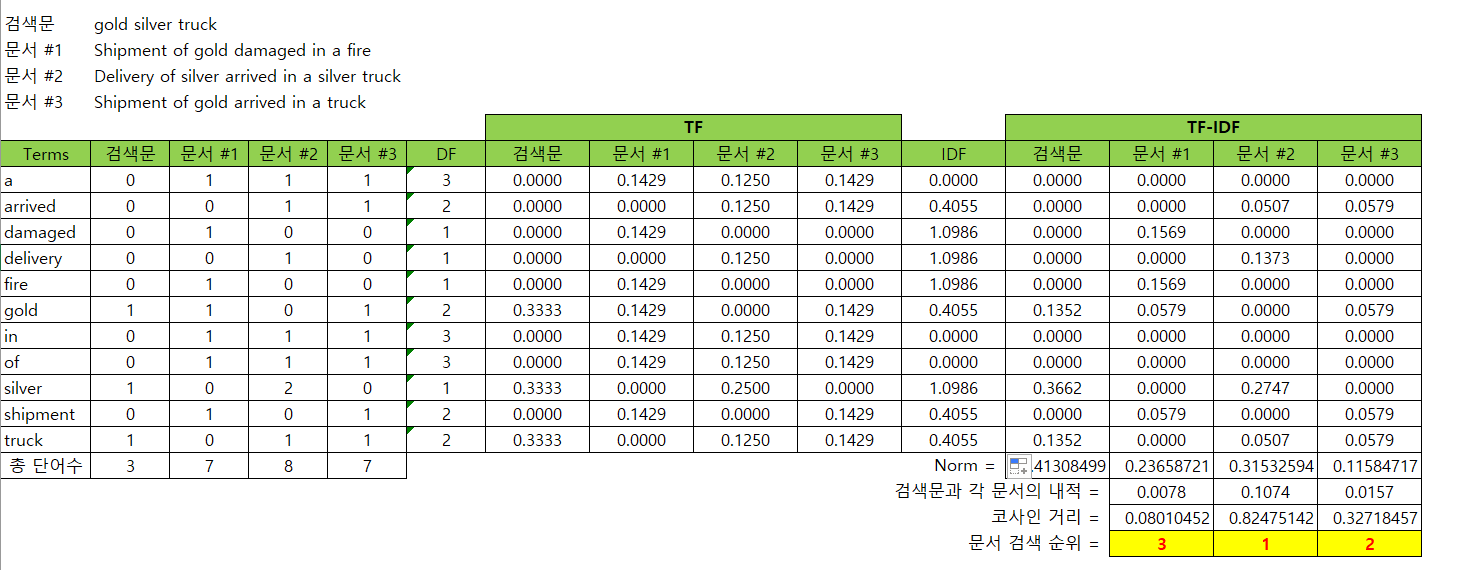
TF(Term Frequency)
문서별 단어의 등장 빈도를 나타내는 행렬이다.
- 어휘 집합(Vocabulary)을 만든다. 모든 문서에 사용된 단어를
행 방향으로 나타낸 것이다. 문서 corpus에 쓰인 모든 단어의 개수가 곧 행의 개수이다. 열 방향으로 단어의 등장 빈도를 기록한다. 즉, 각 문서별로 해당 단어가 몇 번 쓰였는지 나타낸다.
행렬의 마지막 칸에 해당 단어가 총 몇 번 등장했는지 합을 구하고, 그 합을 문서에 등장한 총 단어 수로 나눠 준다. 문서가 길수록 단어의 등장 빈도가 높기 때문에, 문서 길이로 표준화하는 작업이다.
IDF(Inverse Document Frequency)
DF란, 단어의 문서별 등장 빈도를 나타내는 행렬이다. Vocabulary에 있는 모든 단어가 문서 중 몇 개에 등장했는지를 나타낸다.
위의 엑셀 예시에서 ‘silver’의 경우는 두 번째 문서에 2번 등장했지만, 문서 1, 2, 3 중 총 2번 문서에만 등장하므로 DF가 1이 된다.
DF가 클수록 여러 문서에 나타나는 일반적 (general)인 단어라고 본다. 특정 문서 안에서 단어가 많이 나타나면 그 단어는 그 문서 안에서 중요한 단어이긴 하나, 모든 문서에서 그 단어가 많이 나타난다면 그렇지 않을 수 있다. 예컨대, 영어로 치면 a, the와 같이 중요하지 않은 단어일 수 있다.
따라서 specific한 단어일수록 중요도가 크다고 보고, 1/DF에 비례할수록 단어의 중요도가 커진다고 본다. 따라서 IDF 행렬은 Document Frequncy에 역수를 취해 그에 비례하도록 수치를 계산한다. 정확한 계산 공식은 다음과 같다.
TF-IDF
결과적으로 TF-IDF 알고리즘은 단어의 중요도는 TF와 IDF에 비례한다고 본다. 이 때, IDF에 비례한다는 말은, 곧 DF에 반비례한다는 말이기도 하다. 따라서 단어의 중요도를 나타내기 위해 TF와 IDF를 곱한 행렬을 만든다. 이를 TF-IDF 행렬이라고 한다.
TF-IDF 행렬을 구하면, 각 문서별로 단어가 몇 번 등장하는지를 수치화함으로써 해당 문서를 수치화할 수 있게 된다. 이렇게 수치화한 문서 벡터를 다른 작업에 활용한다. 예컨대, 각 문서 벡터 간 유사도를 계산해 검색 문장과 가장 유사한 문서를 추천하는 데에 사용할 수 있다.
2. 구현
파이썬의 Scikit-learn 라이브러리에 TfidfVectorizer 함수를 사용하면 된다. 다만, 이 함수를 사용하면 우리가 위에서 개념적으로 본 것과 TF-IDF 행렬의 행과 열이 반대가 된다. 원리를 익히기 위해, 교재 엑셀 파일과 같은 결과가 나오도록 직접 코딩해보자. 검색 문장을 입력했을 때 1, 2, 3번 문서 중 가장 유사도가 높은 문서가 검색되도록, 문서별 검색 순위를 구해 보자.
나의 풀이
정말 직관적으로 하라는 대로 구현했다. 그런데 행렬 인덱싱 이용해 하려다 보니 코드가 약간 지저분해 보인다. 내장 함수, 라이브러리 등 다른 함수 적극적으로 사용했으면 더 쉬웠을 것 같다. 곧이 곧대로 하려다 보니, 재현성이 떨어지고(transpose 등을 많이 썼다) 코드가 효율적이지 못해 보이는 (느낌적인) 느낌이다.
import numpy as np
# vocabulary 생성
def build_dictionary(corpus):
vocab_dict = {}
for c in corpus:
vocabs = c.strip().split() # 각 문장 어휘 리스트
for vocab in vocabs:
vocab_key = vocab.lower()
if vocab_key not in vocab_dict: # dict 내 어휘, 등장 빈도 색인 생성
vocab_dict[vocab_key] = 0
return sorted(vocab_dict)
# TF 계산
def calc_TF(corpus, vocab_dict):
flag = len(vocab_dict)
# 각 문장별로 단어 등장 빈도 표시한 행렬
TF_matrix = [[v, 0] for _ in range(len(corpus)) for v in vocab_dict] # 초기화
for i in range(len(corpus)):
sent = corpus[i].strip().lower().split()
vocab_cnt = 0 # 어휘 사전에 있는 단어 총 등장 빈도 수
for s in sent:
if vocab in TF_matrix[i*flag : (i+1)*flag]:
if s == vocab[0]:
vocab[1] += 1 # 해당 단어 등장 빈도 업데이트
vocab_cnt += 1 # 총 등장 빈도 업데이트
# 문장 길이로 TF 표준화
for j in range(flag):
TF_matrix[i*flag : (i+1)*flag][j][1] /= vocab_cnt
return TF_matrix
# IDF 계산
def cacl_IDF(corpus, vocab_dict):
IDF_matrix = [[vocab, 0] for vocab in vocab_dict] # IDF 행렬 초기화
for j in range(len(IDF_matrix)):
for i in range(1, len(corpus)):
sent = corpus[i].strip().lower().split()
if IDF_matrix[j][0] in sent: # 문장에 등장하면 등장 빈도 업데이트
IDF_matrix[j][1] += 1
# 공식에 따라 IDF 계산
for i in range(len(IDF_matrix)):
IDF_matrix[i][1] = np.log((len(corpus)-1) / IDF_matrix[i][1]) # 검색 문장 제외
return IDF_matrix * len(corpus) # 이후 계산 편의 위해 형태 변경하여 return
# TF-IDF 계산
def calc_TFIDF(tf, idf, corpus, vocab_dict):
flag = len(vocab_dict)
TFIDF_matrix = []
for i in range(len(corpus)): # 문장별로 tf, idf 구해서 곱하기
tf = np.array([tf[1] for tf in TF[i*flag : (i+1)*flag]], dtype=np.float32)
idf = np.array([idf[1] for idf in IDF[i*flag : (i+1)*flag]], dtype=np.float32)
TFIDF_matrix.append(tf*idf)
return np.array(TFIDF_matrix).T
# 코사인 유사도 계산
def calc_cos_sim(A, B):
# 분자
bunja = A*B
# 분모
norm_A, norm_B = 0, 0
for a in A:
norm_A += a**2
for b in B:
norm_B += b**2
bunmo = np.sqrt(norm_A) * np.sqrt(norm_B)
return (bunja/bunmo).T.sum()
# 각 문서별 코사인 유사도 계산
sentences = [
'gold silver truck',
'Shipment of gold damaged in a fire',
'Delivery of silver arrived in a silver truck',
'Shipment of gold arrived in a truck'
]
dictionary = build_dictionary(sentences)
tf_matrix = calc_TF(sentences, dictionary)
idf_matrix = calc_IDF(sentences, dictionary)
tfidf_matrix = calc_TFIDF(tf_matrix, idf_matrix, sentences, dictionary)
cos_sim_docs = {} # 검색어 문장과의 코사인 유사도 계산해서 저장
for i in range(1, len(sentences)):
cos_sim_docs[sentences[i]] = calc_cos_sim(tfidf_matrix.T[0], tfidf_matrix.T[i])
중헌쓰 풀이
count, norm 등 함수를 적절하게 사용해서 깔끔하게 풀었다. 나도 그냥 count 썼으면 깔끔했을 텐데 왜 그 생각이 안 났을까! 검색 문장과 다른 문장들을 나누어 구현한 점이 신기했다.
import numpy as np
from numpy import dot
from numpy.linalg import norm
Search = input("") # 검색할 문장
DOC1 = str.split('shipment of gold damaged in a fire')
DOC2 = str.split('delivery of silver arrived in a silver truck')
DOC3 = str.split('shipment of gold arrived in a truck')
Terms_raw = DOC1+DOC2+DOC3+str.split(Search) # 모든 문장 합친 raw 문장
Search2 = str.split(Search) # 검색 문장
Terms = list(set(Terms_raw)) # terms 리스트로 만들어 정렬
Terms.sort()
# 중복 제거하기 위해 set 자료구조 활용하고, 단어 빈도 count.
DF = []
for Term in Terms:
DF.append(list(set(DOC1)).count(Term)+
list(set(DOC2)).count(Term)+
list(set(DOC3)).count(Term))
# IDF 행렬 만들어 주기
IDF = []
for df in DF:
IDF.append(np.log10(3/df))
# 각 문서 내 TF 계산
TF1 = []
TF2 = []
TF3 = []
TFsearch = []
for Term in Terms:
TF1.append(DOC1.count(Term)/len(DOC1))
TF2.append(DOC2.count(Term)/len(DOC2))
TF3.append(DOC3.count(Term)/len(DOC3))
TFsearch.append(Search2.count(Term)/len(Search2))
# TF-IDF 계산
TF1_IDF = []
TF2_IDF = []
TF3_IDF = []
TFsearch_IDF = []
for i in range(len(Terms)):
TF1_IDF.append(IDF[i]*TF1[i])
TF2_IDF.append(IDF[i]*TF2[i])
TF3_IDF.append(IDF[i]*TF3[i])
TFsearch_IDF.append(IDF[i]*TFsearch[i])
TF1_IDF= np.array(TF1_IDF)
TFsearch_IDF = np.array(TFsearch_IDF)
def cos_sim(A, B):
return dot(A, B)/(norm(A)*norm(B))
Doc1_ = cos_sim(TFsearch_IDF,TF1_IDF)
Doc2_ = cos_sim(TFsearch_IDF,TF2_IDF)
Doc3_ = cos_sim(TFsearch_IDF,TF3_IDF)
강사님 풀이
오랜만에 다시 보는 클래스… 지금 당장은 무리고 나중에 다시 보자…
import nltk
import math
import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.metrics.pairwise import cosine_similarity
class TextSimilarityExample:
def __init__(self, statements):
self.statements = statements
def TF(self, sentence):
words = nltk.word_tokenize(sentence.lower())
freq = nltk.FreqDist(words)
dictionary = {}
for key in freq.keys():
norm = freq[key] / float(len(words))
dictionary[key] = norm
return dictionary
def IDF(self):
def idf(TotalNumberOfDocuments, NumberOfDocumentsWithThisWord):
return 1.0 + math.log(TotalNumberOfDocuments/NumberOfDocumentsWithThisWord)
numDocuments = len(self.statements)
uniqueWords = {}
idfValues = {}
for sentence in self.statements:
for word in nltk.word_tokenize(sentence.lower()):
if word not in uniqueWords:
uniqueWords[word] = 1
else:
uniqueWords[word] += 1
for word in uniqueWords:
idfValues[word] = idf(numDocuments, uniqueWords[word])
return idfValues
def TF_IDF(self, query):
words = nltk.word_tokenize(query.lower())
idf = self.IDF()
vectors = {}
for sentence in self.statements:
tf = self.TF(sentence)
for word in words:
tfv = tf[word] if word in tf else 0.0
idfv = idf[word] if word in idf else 0.0
mul = tfv * idfv
if word not in vectors:
vectors[word] = []
vectors[word].append(mul)
return vectors
def displayVectors(self, vectors):
print(self.statements, '\n')
for word in vectors:
print("{} -> {}".format(word, np.round(vectors[word], 3)))
def cosineSimilarity(self):
vec = TfidfVectorizer()
matrix = vec.fit_transform(self.statements)
for j in range(1, 5):
i = j - 1
print("\nsimilarity of document {} with others".format(i))
similarity = cosine_similarity(matrix[i:j], matrix)
print(np.round(similarity, 3))
def demo(self):
inputQuery = self.statements[0]
vectors = self.TF_IDF(inputQuery)
self.displayVectors(vectors)
self.cosineSimilarity()
statements = [
'ruled india',
'Chalukyas ruled Badami',
'So many kingdoms ruled India',
'Lalbagh is a botanical garden in India'
]
similarity = TextSimilarityExample(statements)
similarity.demo()
vec = TfidfVectorizer()
matrix = vec.fit_transform(statements)
print('\n')
print(np.round(matrix.toarray(), 3))
print(np.round(matrix.toarray()[0:1]), 3)
print()
for j in range(1, 5):
i = j - 1
print("similarity of document {} with others".format(i))
similarity = cosine_similarity(matrix[i:j, :], matrix)
print(np.round(similarity, 3))
print()


댓글남기기