이레이저

이레이저

[NLP] Transformer_2.Positional Encoding

6 분 소요

출처가 명시되지 않은 모든 자료(이미지 등)는 조성현 강사님의 강의 및 강의 자료를 기반으로 합니다. 논문 출처 


Transformer 이해하기_ Positional Encoding


1. 개요

트랜스포머 모델의 핵심 중 하나는 RNN 네트워크를 제거한 것이었다. RNN 네트워크는 모델 구조 자체가 시퀀스 데이터의 순서를 고려할 수 있게 설계된 것이지만, 이 네트워크를 제거한 이상 입력 문장에서 단어의 순서를 고려할 수 있는 새로운 방법이 필요하다. 그렇지 않다면 모델은 단어의 위치 정보를 알 수 없을 것이다.

따라서 Transformer 모델은 입력 시퀀스의 단어를 임베딩한 뒤, 각 단어의 위치 정보를 모델에 전달하기 위해 Positional Encoding 벡터를 사용한다. 쉽게 이해하자면, 임베딩 벡터에 위치 별로 특정한 패턴을 나타내는 Positional Encoding 벡터를 덧대는 것이다. Transformer 모델에서 인코더와 디코더의 입력은 모두 Positional Encoding 단계를 거치게 된다.

Since our model contains no recurrence and no convolution, in order for the model to make use of the order of the sequence, we must inject some information about the relative or absolute position of the tokens in the sequence. To this end, we add “positional encodings” to the input embeddings at the bottoms of the encoder and decoder stacks.


2. 방법

Positional Encoding을 구현할 수 있는 방법은 여러 가지가 있다. 학습을 통할 수도 있고(learned), 항상 고정된 위치의 값을 인코딩으로 사용할 수도 있다(fixed). 논문에서는 후자의 방법을 택한다. 학습을 통한다기 보다는, 조건을 만족하는 방식에 따라 각 단어의 위치에 일종의 번호를 부여한다는 의미이다.

Positional Encoding은 각 단어의 위치를 나타내기 때문에, 기본적으로 다음의 조건을 만족해야 한다.

  • 각 문장에서 단어의 위치마다 유일한 encoding 값이 출력되어야 한다.
  • 각 단어 위치 간 거리가 일정해야 한다.


이제 인코딩 값을 어떻게 줄 수 있을지 생각해 보자. 먼저 스칼라를 사용할 수 있다.

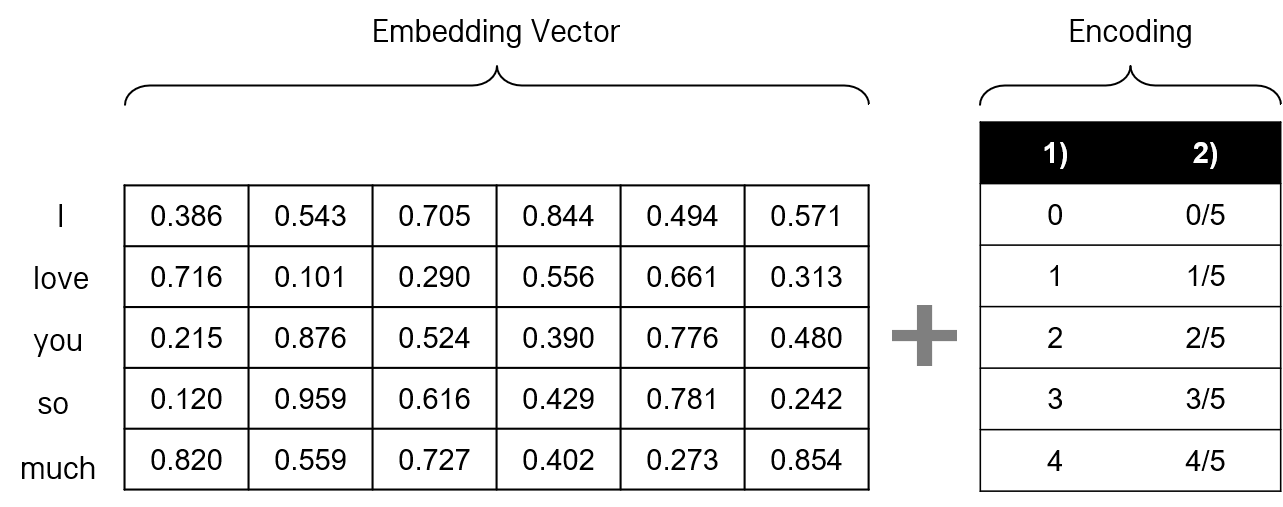
Scalar-Pos-Encoding

첫째, 단순히 문장 내 단어 번호별로 숫자를 붙인다. "I love you so much"와 같은 문장의 경우, 각각의 단어의 위치를 나타내는 인코딩 숫자로서 I에 0, love에 1, you에 2와 같이 위치 인덱스를 사용하는 것이다. 그러나 문장이 길어질수록 숫자가 커질 수 있고, 인코딩 값의 스케일이 맞지 않아 훈련 시 사용했던 값보다 큰 값이 입력 값으로 들어오게 되면 문제가 발생한다.

둘째, 문장 번호별로 숫자를 붙이고, 스케일 조정을 위해 단어의 개수로 나눠 준다. 위와 동일한 "I love you so much" 문장의 경우, I에 0/5, love에 1/5와 같은 방식으로 위치 인덱스를 사용하는 것이다. 각 단어를 나타내는 인코딩 간 거리가 동일하고, 스케일도 조정되어 있다. 그러나 단어 임베딩 벡터의 차원 \(d_{model}\) 이 커질수록 1차원의 벡터(이자 스칼라)로만 표현된 순서 정보는 의미 정보인 임베딩 벡터에 비해 두각을 드러내지 못한다.


이를 통해 위의 두 조건에 더해, 각 Positional Encoding은 단어의 의미 정보와 함께 모델에 전달되더라도 위치 정보를 부각할 수 있도록 (조금 더 쉽게 말하자면, 위치 정보가 묻히지 않도록) 이루어져야 한다는 것을 알 수 있다. 이를 위해 임베딩과 같은 차원의 벡터로 단어의 순서 정보를 인코딩한다.


그래서 단어 임베딩과 같은 차원의 벡터로 Positional Encoding을 구현하기 위해, 아래 그림에서와 같이 위치 정보를 찾아낼 수 있는 벡터를 찾아 나간다.

positional encoding 2

우선, 각 벡터 간 거리가 일정해야 한다. 이를 위해 원점으로부터 초기 벡터를 찾고, 원점과 초기 벡터 간 동일한 거리를 갖는 벡터를 찾는 방식을 택한다. 따라서 Positional Encoding된 각 벡터 간 거리가 동일해야 한다. 동시에, 각 위치가 서로 다른 위치에 종속되면 안 되므로, 각 벡터 간 내적이 동일해야 한다. 위치 정보 벡터들이 서로 독립적이어야 함을 의미한다.

또한, 각 벡터가 원점으로부터 발산하지 않아야 한다. 내적이 동일한 벡터를 찾아 나가기 위해 동일한 일직선 상에서 벡터를 선택한다고 생각해 보자. 나중에는 계산량이 무한히 커질 것이다. 따라서 모든 벡터의 노름이 동일하도록, 이전 벡터에서 다음 벡터를 선택할 때 일정 크기의 각 \(\theta\)을 줘서 선택한다.

어떠한 방식이든 위의 조건을 만족하도록 위치 정보 벡터를 찾아 나가면, 그 결과로 도출되는 각각의 벡터를 Positional Encoding 값으로 사용할 수 있다.


정리하면 다음과 같다. 인코더 입력 문장이 \(d_{model}\) 차원의 벡터로 임베딩된다고 하자. Positional Encoding은 1) 위와 같은 방법론을 따라 선택된, 2) 임베딩된 벡터와 같은 \(d_{model}\) 차원 공간에서의 벡터로서, 3) 각 단어 임베딩과 합쳐져 문장 내 위치 정보를 표현하게 된다. 임베딩 결과에 Positional Encoding을 통해 위치 정보를 추가하는 것이다.

Similarly to other sequence transduction models, we use learned embeddings to convert the input tokens and output tokens to vectors of dimension \(d_{model}\). (…) The positional encodings have the same dimension \(d_{model}\) as the embeddings, so that the two can be summed.


3. 구현

논문은 위와 같은 방법론에 따라 이상적인 조건을 만족하는 Positional Encoding 기술을 구현한다.


\(PE_{(pos, 2i)} = sin(pos/10000 ^ {2i/d_{model}}) \\ PE_{(pos, 2i+1)} = cos(pos/10000 ^ {2i/d_{model}})\)

\(pos\) 는 각 단어가 문장 내에서 몇 번째 단어인지를 의미하며, \(i\) 는 임베딩 벡터의 차원에서의 순서를 나타낸다. 예컨대, "I love you so much"의 문장 내 각 단어를 128차원으로 임베딩했다면 \(pos\) 는 0부터 4까지, \(i\) 는 0부터 127까지가 될 것이다.

\(sin\), \(cos\) 함수를 이용하기 때문에, 각 값이 모두 -1에서 1 사이로 통일되어 벡터가 발산하지 않는다. 또한, 홀수 인덱스의 경우 \(cos\) 함수의 주기를, 짝수 인덱스의 경우 \(sin\) 함수의 주기를 이용하기 때문에 각각의 값들이 모두 다르게 인코딩되며, 상대적인 위치 정보를 전달할 수 있게 된다. \(i\) 에 따라 크기가 바뀌는데, \(i\) 가 증가하는 크기가 일정하므로, 각 벡터 간 거리도 일정해 진다. (자세한 수학적인 증명이 나중에 알고 싶어 진다면, 여기를 참고하자.)


그렇다면 이것을 코드로 어떻게 구현할 수 있는지 알아 보자. 논문을 발표한 Google에서 공개한 Positional Encoding 코드는 다음과 같다.

import numpy as np

def get_angles(pos, i, d_model):
    angle_rates = 1 / np.power(10000, (2 * (i // 2)) / np.float32(d_model))
    return pos * angle_rates

def positional_encoding(position, d_model):
    angle_rads = get_angles(np.arange(position)[:, np.newaxis],
                            np.arange(d_model)[np.newaxis, :],
                            d_model)

    # apply sin to even indices in the array; 2i
    sines = np.sin(angle_rads[:, 0::2])    
    # apply cos to odd indices in the array; 2i+1
    cosines = np.cos(angle_rads[:, 1::2])
    
    pos_encoding = np.concatenate([sines, cosines], axis=-1)

    return pos_encoding

get_angles 함수를 통해 단어의 위치에 따라 \(sin\), \(cos\) 함수 안에 들어갈 중심각의 크기를 구한다. 임베딩 벡터와 같은 크기의 텐서를 만들어야 하는데, 이 텐서의 행은 문장의 길이, 열은 임베딩 벡터의 차원이 될 것이다. positional encoding에서 pos를 행으로, i를 열로 하는 행렬로 만들고 각 위치를 전달한다. sines와 cosines에서는 각각 i가 0부터 시작해 2씩 증가하는 짝수 위치의 인덱스, 1부터 시작해 2씩 증가하는 홀수 위치의 인덱스에 대해 \(sin\) 값과 \(cos\) 값을 구한다. 그리고 각각의 값을 concat한다.


실제로 이렇게 만들어진 각 벡터가 무엇인지, 그 벡터 간 거리와 각 벡터의 크기는 일정한지 확인해 보자.

먼저, 위에서 예로 든 "I love you so much"의 문장을 6차원의 벡터로 임베딩하고, 그에 대한 Positional Encoding 벡터를 구해 보자.

PE = positional_encoding(5, 6)
print(PE.round(3))

# Positional Encoding 벡터
[[ 0.     0.     0.     1.     1.     1.   ]
 [ 0.841  0.046  0.002  0.54   0.999  1.   ]
 [ 0.909  0.093  0.004 -0.416  0.996  1.   ]
 [ 0.141  0.139  0.006 -0.99   0.99   1.   ]
 [-0.757  0.185  0.009 -0.654  0.983  1.   ]]


그리고 각 벡터의 크기, 내적을 구해 보자.

from sklearn.metrics.pairwise import euclidean_distances

for i in range(PE.shape[0] - 1):
    d = euclidean_distances(PE[i].reshape(1,-1), PE[i+1].reshape(1,-1))
    norm = np.linalg.norm(PE[i])
    dot = np.dot(PE[i], PE[i+1])
    print("%d - %d : distance = %.4f, norm = %.4f, dot = %.4f" % (i, i+1, d[0,0], norm, dot))

모두 동일한 것을 알 수 있다.

# 각 벡터 간 거리, 각 벡터의 노름, 내적
0 - 1 : distance = 0.9600, norm = 1.7321, dot = 2.5392
1 - 2 : distance = 0.9600, norm = 1.7321, dot = 2.5392
2 - 3 : distance = 0.9600, norm = 1.7321, dot = 2.5392
3 - 4 : distance = 0.9600, norm = 1.7321, dot = 2.5392


이제 정말 각 벡터가 동일한 간격을 보이는지, 원점에서 어느 같은 거리에 있는지 확인해 보자. 위와 같은 예에서는 6차원이므로 시각화하기 어렵기 때문에 2차원 그림을 그려 본다.

import matplotlib.pyplot as plt

PE = positional_encoding(32, 2)
plt.figure(figsize=(8, 8))
plt.plot(PE[:, 0], PE[:, 1], marker='o')
plt.show()

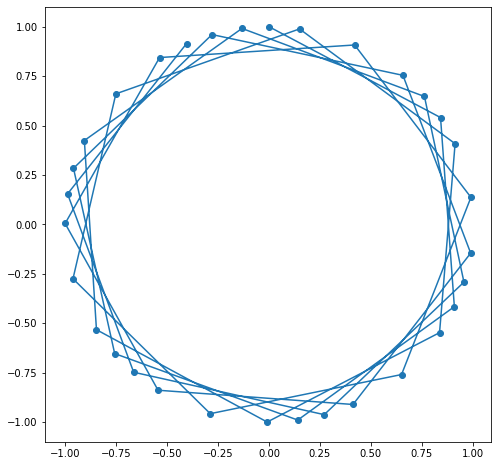
2d-positional-encoding

 실제로 뺑글 뺑글 원을 그리며 돈다!


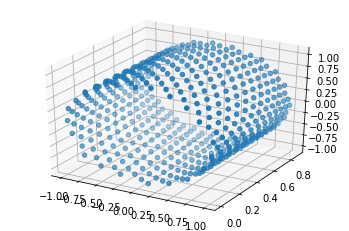
3차원으로도 나타내 보자.

fig = plt.figure()
ax = fig.gca(projection='3d')

PE = positional_encoding(500, 3)
plt.figure(figsize=(12, 12))
ax.scatter(PE[:, 0], PE[:, 1], PE[:, 2], marker='o')
plt.show()

3d-positional-encoding

실제로 뺑글 뺑글하게 입체 도형을 만들며 돈다!


참고

Positional Encoding을 반드시 위의 공식으로만 구현할 수 있는 것은 아니다. 또 다른 Positional Encoding에 대해 다른 논문들도 많이 있다. 기본적으로 각 벡터 간 등간격 거리(equidistant)가 되도록 하는 게 조건이다.



hit count image

댓글남기기

참고