[ML/DL] Sigmoid 함수
멀티캠퍼스 나용찬 교수님의 빌드업 특강 자료를 기반으로 합니다.
Sigmoid 함수의 도출
로지스틱 회귀 알고리즘은 다음과 같은 sigmoid 함수를 이용하여 이진 분류 작업을 수행한다.
\(\sigma(t) = \frac {1} {1+exp(-t)}\)
이 때 \(t\)는 linear regression에서의 선형회귀식 \(H(x) = w \cdot x + b\)으로부터 도출된 값이다. 즉, 입력 데이터 x를 선형회귀식에 넣은 뒤 구한 다음의 값이 sigmoid 값이라는 것이다.
\(\frac {1} {1+exp(-w \cdot x + b)}\)
이 sigmoid 함수는 다음과 같이 S자 형태를 띠게 된다.
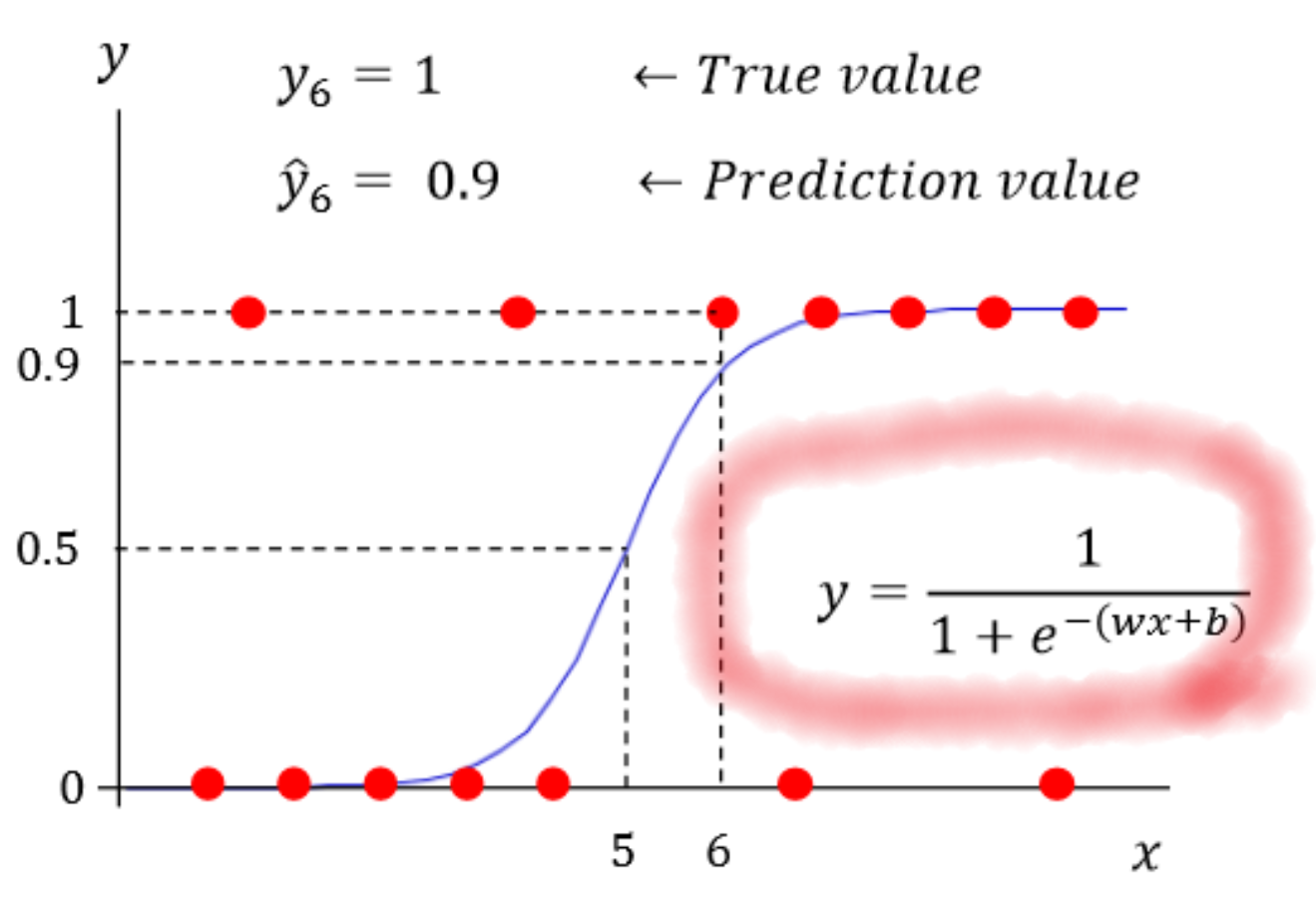
이 함수에 의해 선형회귀식에 의해 도출된 결과 값은 0과 1 사이의 값으로 바뀌게 된다. 이렇게 도출된 결과값을 로짓(logit)이라고 부르며, 로지스틱 회귀 모형은 다음의 원리에 따라 해당 로짓 값이 0.5 이상이면 양성 클래스(혹은 1), 미만이면 음성이라고 예측하는 것이다.
\(\hat{y} = \begin{matrix}
0, \ \ \hat{p} < 0.5 \\
1, \ \ \hat{p} \geq 0.5
\end{matrix}\)
이제, sigmoid 함수가 어떻게 선형회귀식에 의해 도출된 값을 0과 1 사이의 확률 값으로 변화시키는지 알아보자. 트릭을 사용할 것이다!
1. odds 사용
우리의 목표는 선형회귀식 \(H(x)=ax+b\)의 결과값을 $0$과 $1$사이의 확률 $P$로 변환하는 것이다. 그래야 양성일 확률이 얼마인지 알 수 있고, 그 확률이 어디에 어디에 가까운지에 따라 클래스를 판정할 수 있기 때문이다.
선형회귀식에 의해 도출된 값은 \(-\infty\)와 \(\infty\) 사이의 값을 갖는다. 따라서 sigmoid 함수를 도출하는 과정은 선형회귀식에 의해 도출된 값의 범위를 바꿔 주는 것과도 같다. 이를 위해, 확률 \(P\)를 승산으로 표현해 보자.
승산이란, 사건이 일어나지 않을 가능성 대비 사건이 일어날 가능성으로, 확률을 표현하는 방법 중 하나다.
\(odds = \frac {P} {1-P}\) 이렇게 승산을 활용하게 되면, 선형회귀식의 값을 $0$에서 $\infty$ 사이의 값으로 바꿀 수 있다.
\[\frac {P} {1-P} = ax+b\]2. 로그 승산
여전히 좌변의 값의 범위가 0부터 1이 되지 않는다. 그러므로, 승산 대신 승산에 로그를 취한 값인 log odds 값을 사용하자. $0$에서 $\infty$ 사이의 값에 로그를 취하므로, $log(odds)$의 값은 $-\infty$와 $\infty$ 사이의 값이 된다. 이제 양변의 값의 범위가 일치한다.
\(log(\frac {P} {1-P}) = ax+b\)
3. P에 대한 식으로 변환
우리가 알고 싶은 것은 양성일 확률 $P$이다. 따라서 양변을 $P$에 대해 정리한다.
\[e^{log(\frac {P} {1-P})} = e^{ax+b}\] \[\frac {1-P} {P} = e^{ax+b}\] \[\frac {1} {P} = \frac {1+e^{ax+b}} {e^{ax+b}}\] \[P = \frac {e^{ax+b}} {1+e^{ax+b}}\]마지막 식의 우변의 분자, 분모 각각에 $e^{-(ax+b)}$를 곱하면, 우리가 알고 있는 sigmoid 식이 된다.
추가 : 20200617 조성현 강사님 강의 내용 추가
sigmoid 함수를 활용하는 이진 분류 문제에서는 log loss, 즉, cross entropy를 손실함수로 사용한다.
데이터가
n개가 있다고 할 때, 크로스 엔트로피 식을 해석해 보자.
실제 레이블
y가 1일 때,y_hat이 0이면 CE 식의 앞 부분만 남게 되고, cost가 무한대가 된다. 반대로 실제 레이블y가 0일 때,y_hat이 1이라면 CE 식의 뒷 부분만 남게 되고, cost는 무한대가 된다. 즉, 클래스를 틀리게 예측하면 할수록 cost값이 매우 커지게 되며 penalty를 주는 것이다.

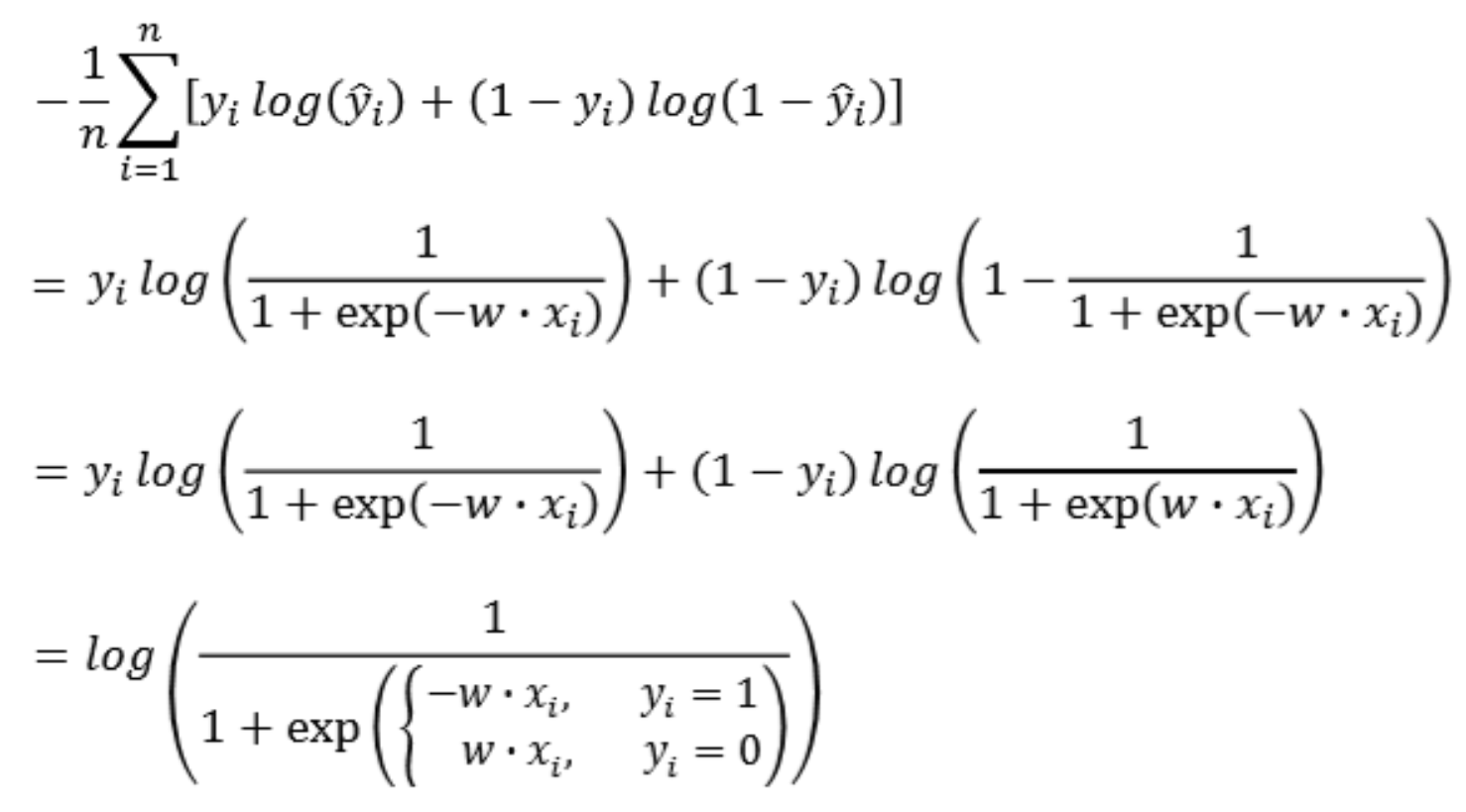

댓글남기기