[Algorithm] 그리디(탐욕) 알고리즘

개념

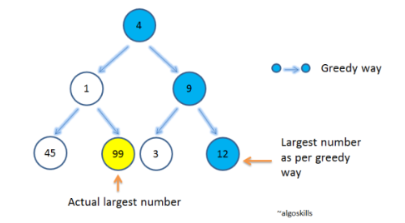
탐욕 알고리즘은 각 상황에서 최선의 결정을 하여, 최종적으로 최적의 해를 찾아내는 방식이다. 미래를 생각하지 않고, 각 단계 단계만 생각한다고 하여 탐욕적이라고 한다.

엄밀히 말하면, 버블 정렬, 퀵 정렬과 같이 구체적인 알고리즘이라기 보다는, 문제를 해결하는 논리 설계 방식에 가깝다고 본다. 주로 최적화(최댓값 혹은 최솟값) 문제를 해결하는 데 사용한다.

특징

• 한 번 이루어진 선택에 대하여 번복하지 않는다.
• 각 지점에서 이루어지는 선택은 지역적으로 최선이다.

각 단계별로 이루어지는 최적의 선택이 전체 문제에서도 최적이 될 것이라는 가정을 바탕으로 한다.

당연히 항상 최적의 해를 구할 수는 없다 는 단점이 있다.

마치, 지금 방탄소년단 콘서트를 가면 무척 행복하고, 그것이 최적이지만, 나중에 시험 공부를 못 해서 성적이 나오지 않으면 최적이 아니게 되는 것처럼(?)

다만, 완전 탐색(브루트 포스)처럼 모든 경우의 수를 다 검사하지 않기 때문에 속도가 빠르다 는 장점이 있다.

적용

위와 같은 특징으로 인해 그리디 알고리즘은 제약과 조건이 있는 경우 제한적으로 적용된다. 그 의미는,

• 최적해 를 구하는 문제여야 하며,
• 그 과정에서 단계별로 내린 결정이 다음 단계의 결정에 영향을 미치지 않아야 하는,

문제여야 한다는 것이다.

대표적으로 적용할 수 있는 문제 유형은 다음과 같다.

활동선택

한 번에 하나의 활동만 처리할 수 있는 상황에서, 제안된 활동들을 해결하기 위한 최적의 방법을 구하는 문제이다.

거스름돈 문제

가장 적은 수의 화폐를 사용해 거스름돈을 거슬러 주는 문제이다. 일반화하면, 전체를 크기가 다른 여러 개의 부분으로 채울 때, 그 부분들의 개수가 최소가 되도록 하는 문제라고 볼 수 있다.

실제로 풀어 보면, 주어진 데이터를 정렬하고, 최적의 경우를 찾아 나감으로써 해결된다. 혹은, 일상 생활에서 우리가 생각하는 최적의 경우를 찾는 방식을 그대로 구현하면 된다.

적용할 수 없는 문제의 대표적인 유형으로는 배낭 문제, 외판원 문제, 거스름돈 사이에 약수와 배수 관계가 성립하지 않는 거스름돈 문제 등이 있다.

사용

문제를 보면 처음으로 생각하게 되는 논리가 대부분 그리디 알고리즘이다. 물론 문제를 많이 풀어 보고, 그리디 알고리즘을 적용할 수 있는 문제의 유형들을 어렴풋이나마 구분할 줄 안다는 것을 전제로 한다.

만약 그리디 알고리즘을 적용했는데도 풀리지 않는 문제가 있다면, 그 때는 동적 프로그래밍(DP), 다익스트라 알고리즘 등을 사용해 접근하도록 한다.