[Algorithm] 삽입정렬

개요

자료 내 모든 원소들을 앞에서부터 차례대로 이미 정렬된 부분과 비교하여, 자신의 위치를 찾아냄으로써 정렬을 완성하는 알고리즘이다. 도서관 사서가 책을 정렬할 때 일반적으로 활용되는 정렬 방식이다.

사람의 머리로 이해하기는 간단하지만, 코드로 구현했을 때 효율성이 떨어진다.

^{출처 : http://ejklike.github.io/2017/03/04/sorting-algorithms-with-python.html}

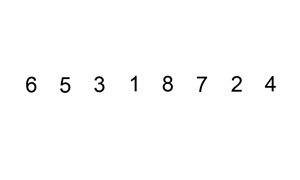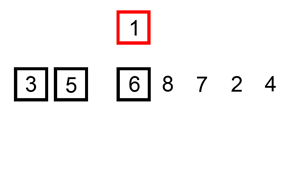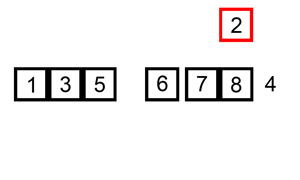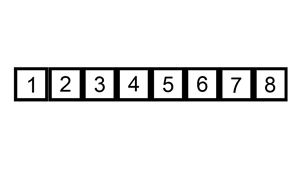
원리

정렬을 수행하는 방법은 다음과 같다.

1. 정렬할 자료를 부분집합 S, U로 나눈다.
   • S : 이미 정렬된 앞 부분 원소들. 초기 상태에는 첫 번째 원소를 S로 간주한다.
   • U : 아직 정렬되지 않은 나머지 원소들.
2. U의 원소들을 하나씩 꺼내서 S의 마지막 원소부터 비교하면서 위치를 찾는다.
3. 2의 과정을 반복하며, S의 원소는 하나씩 늘리고 U의 원소는 하나씩 감소시킨다.
4. U가 공집합이 되면 모든 삽입정렬 과정이 완료된다.

예) 69 10 30 2 16 8 31 22를 오름차순으로 삽입정렬하는 과정

정렬 원소 미정렬원소

S	U	위치	정렬 결과
69	10 30 2 16 8 31 22	10 < 69	10 69 30 2 16 8 31 22
10 69	30 2 16 8 31 22	30 < 69, 30 > 10	10 30 69 2 16 8 31 22
10 30 69	2 16 8 31 22	2 < 69, 2 < 30, 2 < 10	2 10 30 69 16 8 31 22
2 10 30 69	16 8 31 22	16 < 39, 16 < 30, 16 > 2	2 10 16 30 69 8 31 22
…	…	…	…

시간 복잡도

각 부분집합의 원소를 매번 비교해야 하므로, O(N^2)의 시간 복잡도를 가진다. 다만, 평균적으로 버블정렬보다는 빠르다.

데이터가 이미 정렬되어 있는 경우라면 O(N)의 시간 복잡도를 보이지만, 역순으로 정렬된 경우 삽입을 위해 값을 하나씩 밀어내야 하는 과정을 반복해야 하므로 매우 느리다.

코드 구현

• 내부 반복문에서는 새롭게 추가된 값보다 작은 숫자를 만나는 최초의 순간까지 뒤에서부터 비교하며, 앞의 값이 뒤의 값보다 클 경우 자리를 바꾼다. 앞에서 뒤로 진행한다.
  • 앞에 있는 숫자들은 기존에 정렬을 해 놓았기 때문에, 최초로 작은 숫자를 만난다면 앞으로 갈 필요가 없다.
  • 값을 바꿀 때는 버블정렬처럼 swap하지 않고, 값의 위치를 shift한다. 즉, 앞의 값을 뒤로 밀다가 최초로 작은 값을 만난 순간 추가되는 값을 넣는다.
• 외부 반복문에서는 정렬 범위를 2에서 끝까지 확대해 나간다. 뒤에서 앞으로 진행한다. 버블 정렬과 달리 정렬 범위가 넓어진다.

def InsertionSort(a):
    for end in range(1, len(a)):
        to_insert = a[end] # 비교하려는 값.
        i = end # 비교하려는 값의 인덱스.
        while i > 0 and a[i-1] > to_insert:
            arr[i] = arr[i-1]
            i -= 1
        arr[i] = to_insert