[Algorithm] 병합정렬

여러 정렬된 자료의 집합을 병합해ㅔ 한 개의 정렬된 집합으로 만듦.

분할정복 알고리즘 활용

자료를 최소 단위 문제까지 나눈 후 차례대로 정렬하여 최종 결과를 얻음. top-down 접근 방식.

O(nlogn)

연결 리스트 사용해 구현.

동작 과정

1. 분할 : 전체 자료 집합을 최소 부분집합이 될 때까지 분할 작업 계속 진행.

(그림)

1. 병합 : 2개의 부분집합을 정렬하면서 하나의 집합으로 병합. 모든 부분집합이 1개로 병합될 때까지 반복.

(그림)

69 10 30 2 16 8 31 22를 병합 정렬하는 과정

분할

전체 자료 집합에 대해 최소 크기 부분집합이 될 때까지 분할 작업 계속 : 크기가 1인 부분집합이 될 때까지 : 69 10 30 2 16 8 31 22

병합

2개의 부분집합을 정렬하면서 하나의 집합으로 병합

10 69 / 2 30/ 8 16/ 22 31/

2 10 30 69/ 8 16 22 31

2 8 10 16 22 30 31 69

알고리즘

분할: 재귀 호출 과정에서는 리스트의 길이가 1인 경우와 아닌 경우를 구분. 리스트의 경우가 1이면 종료 조건으로 입력된 리스트 그대로 반환. 길이가 1이 될 때까지 병합정렬 재귀 호출.

그렇지 않다면 분할에서 오른쪽과 왼쪽에 대해 재귀 호출.

그 결과로 반환된 리스트는 정렬된 상태가 된다.

두 개의 리스트를 머지 함수를 이용해 하나의 리스트로 반환.

def MergeSort(a):
    if len(a) <= 1: # 사이즈가 0이나 1인 경우 바로 리턴.
        return a
    
    # 1. 분할 부분
    mid = len(a)//2
    left = a[:mid]
    right = a[mid:]
    # 리스트의 길이가 1이 될 때까지 재귀 호출
    left = MergeSort(left)
    right = MergeSort(right)
    
    # 2. 정복 부분 : 분할된 리스트 병합
    return Merge(left, right)

병합

병합 과정 구현 시 사용되는 리스트 자료 구조로는 배열리스트와 연결리스트가 있음. 배열 사용 시 분리/병합 과정에서 빈번한 자료 비교 연산과 이동 연산 발생으로 비효율적. 따라서 연결 리스트로 구현함으로써 배열 사용시 단점 극복하여 효과적인 극복 가능.

연결 리스트로 저장된 자료들에 대한 병합 과정

def Merge(left, right):
    result = [] # 두 개의 분할된 리스트를 병합하여 result를 만듦.
    
    while len(left) > 0 and len(right) > 0 : # 양 쪽 리스트에 원소가 남아 있다면
        # 두 하위 리스트의 첫 원소를 비교해 작은 것부터 result에 추가.
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
            
    if len(left) > 0 : # 왼쪽 리스트에 원소 남아 있으면
        result.extend(left)
    if len(right) > 0 : # 오른쪽 리스트에 원소 남아 있으면
        result.extend(right)
        
    return result

카운팅 정렬(a.k.a 계수 정렬)

원소를 직접 비교하지 않고, 원소들의 개수를 세어 정렬하는 방식이다. 즉, 항목의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 센다.

^{이미지 출처 : https://m.blog.naver.com/PostView.nhn?blogId=dnpc7848&logNo=221439395086&categoryNo=15&proxyReferer=https%3A%2F%2Fwww.google.com%2F}

정렬을 수행하는 방법은 다음과 같다.

1. 항목의 개수를 저장할 COUNTS 배열을 만든다.
   • 이 때 COUNTS를 세기 위한 충분한 공간을 할당하려면, 주어진 집합에서 가장 큰 정수를 알아야 한다.
   • 또한 COUNTS는 정수 항목들로 직접 인덱스되는 배열이어야 한다.
2. 주어진 자료 집합(DATA)에서 각 항목 i가 총 몇 개 있는지 세고, COUNTS의 i번째 칸에 저장한다.
3. COUNTS에서 앞에서 뒤로 가며, i번째 칸의 숫자를 i+1번째 칸에 누적한다. 이 조정 작업이 완료되면, COUNTS 배열의 값은 정렬 후 반환할 배열 TEMP에서 인덱스가 나타내는 i라는 항목이 TEMP 배열의 몇 번째 칸에 들어가야 하는지 보여준다.
4. 주어진 집합 DATA의 마지막 항목부터 정렬한다.
   • 정렬해야 할 각 항목의 값을 i라고 한다.
   • COUNTS의 i번째 칸에 있는 수를 room_number한다.
   • TEMP의 room_number칸에 i를 삽입한다.
   • COUNTS의 i번째 칸에 있는 수를 1 감소시킨다.

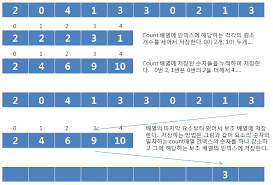
예) 0 4 1 3 1 2 4 1를 오름차순으로 카운팅정렬하는 과정

• DATA : [0 4 1 3 1 2 4 1]

• COUNTS : [1 4 5 6 8]

  • 조정 전 COUNTS : [1 3 1 1 2]
  • 조정 전 COUNTS의 인덱스는 DATA의 항목을 나타내며, 값은 각 항목이 등장한 횟수를 의미한다.

_{파이썬의 리스트 인덱스가 0부터 시작해서 헷갈릴 수 있다. 여기서 COUNTS[i]는 TEMP의 몇 번째 칸인지를 의미한다고 생각하자}

i(정렬할 항목)	COUNTS[i]	TEMP	정렬 후 COUNTS
1	4	_ _ _ 1 _ _ _ _	1 3 5 6 8
4	8	_ _ _ 1 _ _ _ 4	1 3 5 6 7
2	5	_ _ _ 1 2 _ 4	1 3 4 6 7
1	3	_ _ 1 1 2 _ _ 4	1 2 4 6 7
3	6	_ _ 1 1 2 3 _ 4	1 2 4 5 7
1	2	_ 1 1 1 2 3 _ 4	1 1 4 5 7
4	7	_ 1 1 1 2 3 4 4	1 1 4 5 6
0	1	0 1 1 1 2 3 4 4	0 1 4 5 6

코드 구현

• 바깥쪽 반복문에 의해 안쪽 반복문의 범위가 제어된다.
• 한 단계를 마치면 마지막에 정렬이 종료된 원소가 위차하므로, 단계를 거칠수록 정렬의 범위가 1씩 작아진다.

def CountingSort(A):

    counts = [0] * (max(A)+1)
    temp = [0] * len(A)

    # 개수 세서 COUNTS에 저장.
    for a in A:
        counts[a] += 1 # 인덱스로 구현한다면 for i in A: C[A[i]] += 1와 동일.
        
    # COUNTS 조정.
    for i in range(len(counts)-1):
        counts[i+1] += counts[i]
    
    for i in range(len(temp)-1, -1, -1): # reversed(range(len(TEMP)))와 동일
        temp[counts[A[i]]-1] = A[i]
        counts[A[i]] -= 1
    
    return temp

시간 복잡도

시간 복잡도는 O(n+k)로, n은 배열할 항목의 수, k는 항목 중 최댓값을 의미한다.

만약 항목 중 최댓값이 n보다 작으면 시간 복잡도는 O(n)에 가까워지지만, 극단적인 예로 k가 매우 큰 수이면 O(무한)이 될 수도 있다. 따라서 정렬할 수의 최댓값에 영향을 받는 알고리즘이라고 볼 수 있다.

특징

이전까지의 알고리즘과 달리 처음으로 단 한 번의 비교도 수행하지 않고 정렬을 진행하는 알고리즘이다. 그러나 숫자를 세서 저장할 공간이 필요하므로, 메모리 낭비가 야기될 수 있다. 예컨대, 만약 배열이 0, 1, 2, 3, 10억이라면, COUNTS로 (10억+1)칸을 만들어야 한다.

활용

• 정수나, 정수로 표현될 수 있는 자료에 대해서 적용한다. 위의 구현 과정을 통해 살펴보았듯, 정수 항목으로 인덱스되는 발생 횟수들의 리스트를 사용하기 때문이다.
• 원소들의 개수를 세어 정렬하기 때문에, 중복값이 많이 분포되어 있는 배열을 정렬할 때 효과적으로 작용한다.
• 또한, 시간복잡도를 지배하는 것이 배열의 최댓값이기 때문에 정렬할 항목들이 특정한 범위 안에 존재하는 경우 사용한다.

카운팅 정렬을 사용하는 대표적인 예는, 26개의 알파벳으로 이루어진 문자열에서 Suffix Array를 얻는 경우다.

최악의 시간 복잡도는 O(n^2)으로 합병 정렬에 비해 효율이 좋지 못함.

그러나 퀵 정렬인 이유는, 평균 복잡도가 nlogn이기 때문.

	합병 정렬	퀵 정렬
공통점	두 개로 분할해 각각 정렬	두 개로 분할해 각각 정렬
차이점	분할 시 단순히 두 부분으로 나눔.	분할 시, 기준 아이템을 중심으로 작은 것은 왼편, 큰 것은 오른 편에 위치.
	각 부분 정렬 후 합병 후처리작업 필요.	정렬 후 후처리 작업 필요 업슴.