[Algorithm] 퀵정렬

개요

분할 정복 방식을 적용해 정렬을 진행하는 알고리즘이다. 정렬 알고리즘 계의 최고 존엄격으로, 매우 효율적이다.

원리

리스트 중 하나를 피봇으로 선택하고, 피봇보다 작은 원소는 왼쪽에, 큰 원소는 오른쪽에 정렬한다. 이후 피봇값을 중심으로 리스트를 분할하고, 분할된 각각의 리스트에 재귀적으로 이 과정을 반복한다.

이렇게 작은 쪽의 배열, 큰 쪽의 배열 각각에 대해 정렬 과정을 반복하다 보면 각각의 파티션에 정렬된 파티션이 두 개밖에 남지 않게 된다. 이는 정렬이 완료되었음을 의미하며, 각각의 리스트를 작은 리스트로 분할하여 모든 정렬을 완료함으로써 정렬 문제를 정복하게 된다.

^{이미지 출처 : https://www.fun-coding.org/Chapter12-selectionsorting.html}

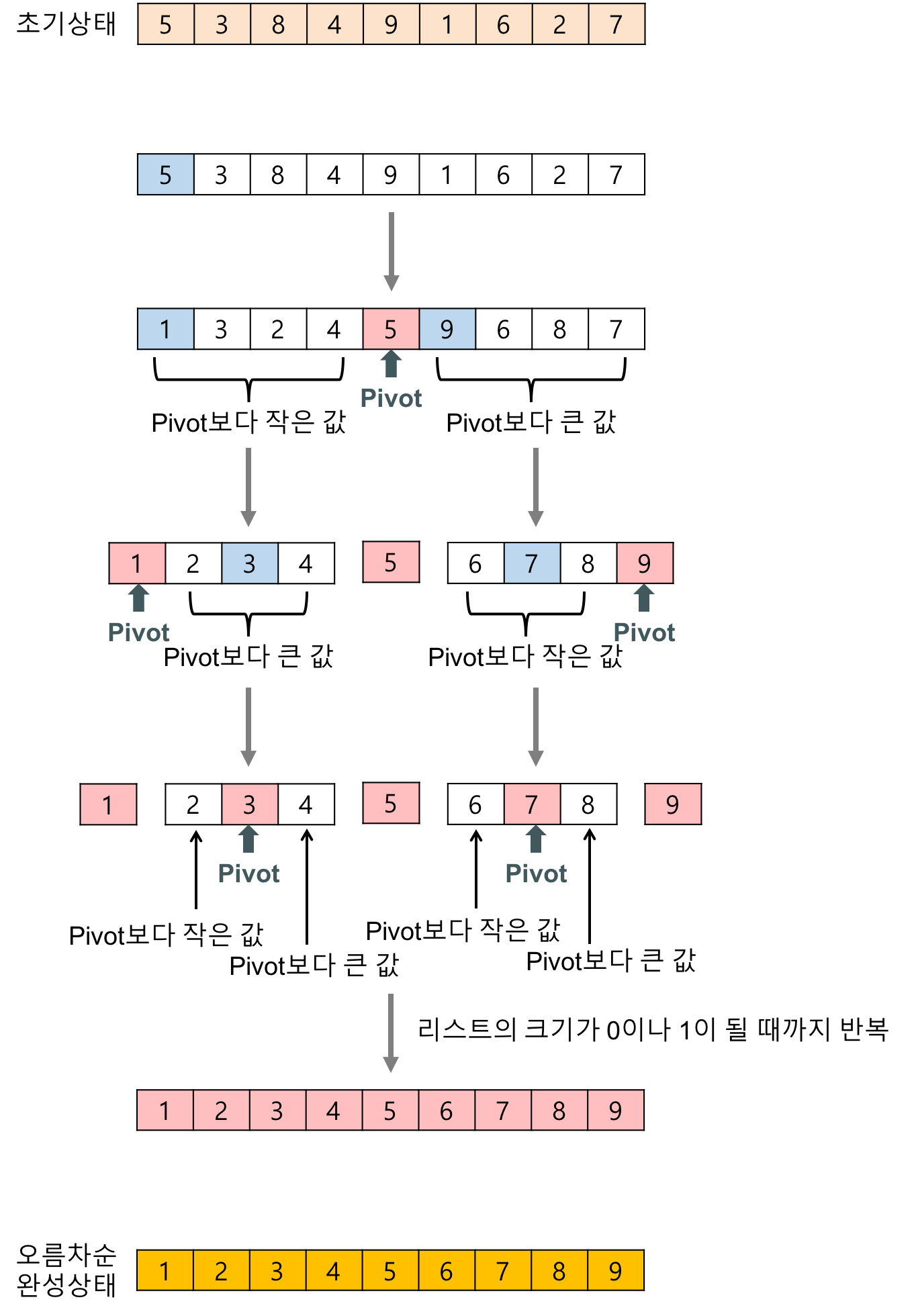
한 단계가 완료될 때마다 피봇의 위치가 확정된다.

정렬 원소 {미정렬 원소}

정렬 대상 리스트	피봇	L	R	정렬 결과
68 11 29 3 15 9 32 23	3	68	68	3 {11 29 68 15 9 32 23} 1. L = R = 68이므로 68과 피봇 교환. 2. 피봇 3의 위치 확정. 3. 피봇 3의 왼쪽은 공집합이므로 ,오른쪽에 대해서만 이후 정렬 수행.
11 29 68 15 9 32 23	15	29	9	3 {11 9 68 15 29 32 23} 1. L과 R이 만나지 않았으므로 위의 작업 반복.
	15	68	68	3 {11 9} 15 {68 29 32 23} 1. L = R = 68이므로 68과 피봇 교환. 2. 피봇 15의 위치 확정. 3. 피봇 왼쪽과 오른쪽에 대해 정렬 수행
11 9	11			3 {9} 11 15 {68 29 32 23} 1. L의 원소가 그 자체로 피봇이므로, 그 자체로 교환이 일어난 것으로 간주. 2. 피봇 11의 위치 확정.
9	9			3 9 11 15 {68 29 32 23} 1. 피봇 9의 위치 확정.
68 29 32 23	29	68	23	3 9 11 15 {23 29 32 68} 1. L과 R이 만나지 않았으므로 위의 작업 반복
	29	29	29	3 9 11 15 {23} 29 {32 68} 1. R의 원소가 그 자체로 피봇이므로 자리 교환 발생. 2. 피봇 29의 위치 확정.
23	23			3 9 11 15 23 29 {32 68} 1. 피봇 23의 위치 확정.
32 68	32	32	32	3 9 11 15 23 29 32 {68} 1. L = R = 32이므로 피봇 32의 위치 확정.
68	68			3 9 11 15 23 29 32 68 1. 피봇 68의 위치 확정.

---

시간 복잡도

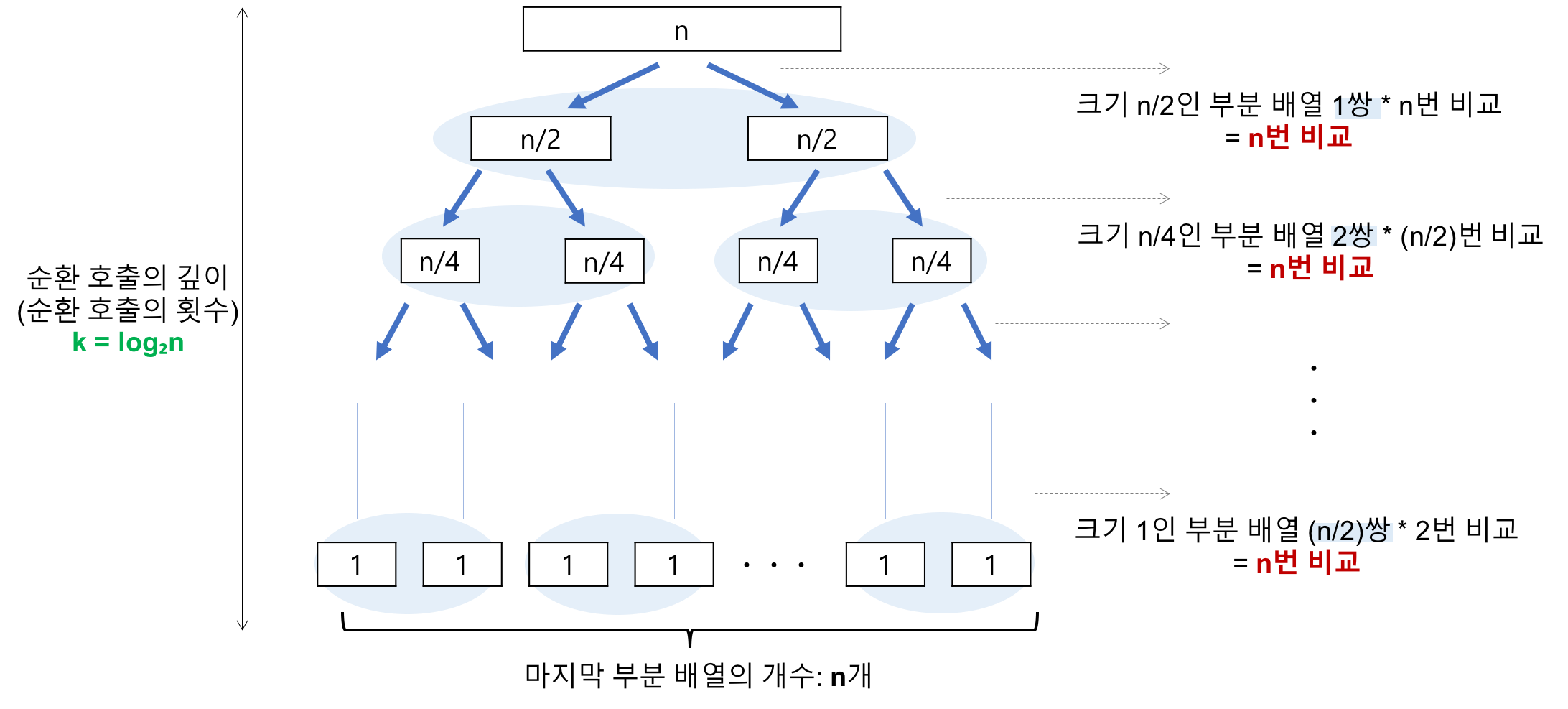
평균적으로O(NlogN)의 시간 복잡도를 가진다.

파티션 안 원소의 개수가 1이 될 때까지 분할하기 때문에, 파티션으로 분할하는 횟수는 N번이다. 따라서 O(N)의 시간을 필요로 한다. 그러나, 한 번 분할할 때마다 탐색해야 할 데이터가 절반씩 줄어들기 때문에 한 번 돌 때 탐색을 위해서는 O(logN)의 시간을 필요로 한다.

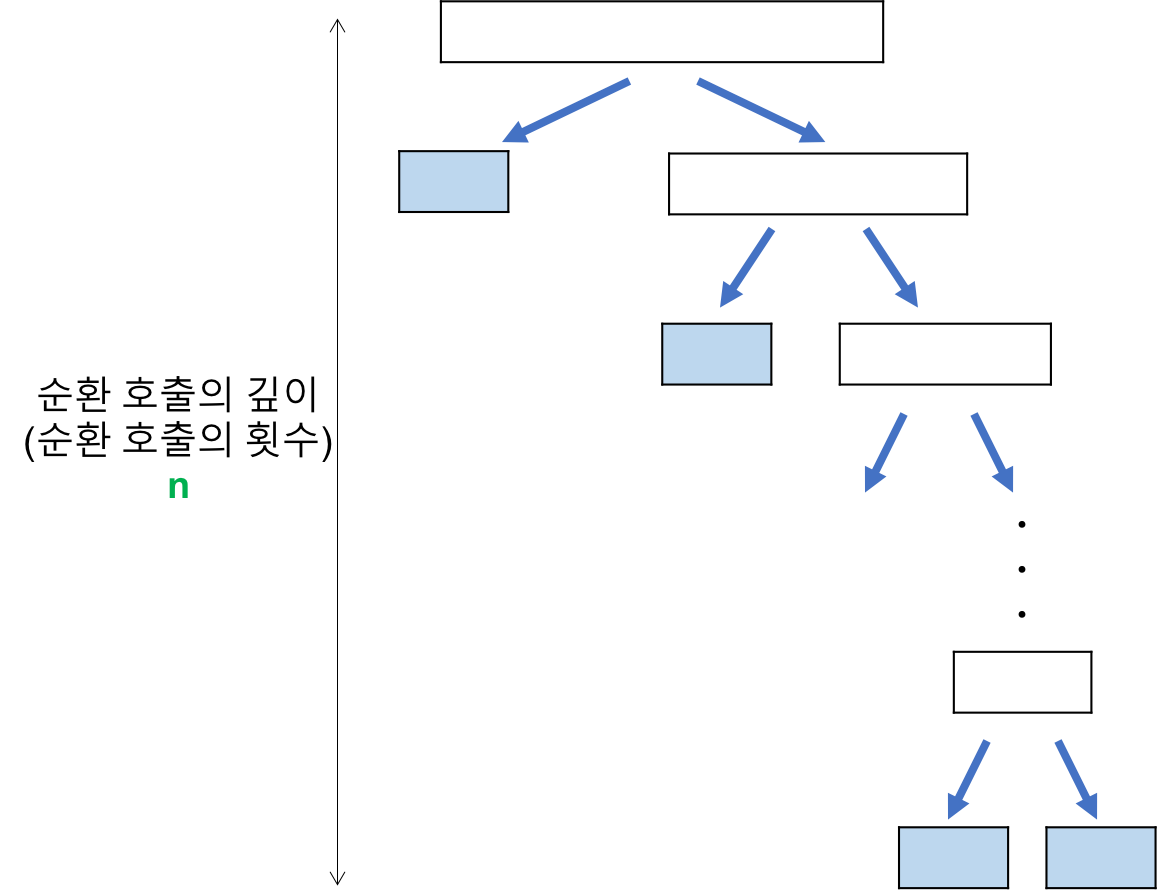
그러나 최악의 경우 O(N^2)의 시간 복잡도를 가진다.

이는 피봇의 왼쪽 요소가 매 번 하나가 되도록 피봇이 선택되는 경우에 발생한다. 이 경우, 우선 N번의 데이터 분할을 진행하여 O(N)의 시간이 필요하다. 이후, N개의 요소에 대해 모두 정렬을 수행해야 하기 때문에 추가적으로 O(N)의 시간이 필요하게 되는 것이다. 피봇을 어떻게 선택하느냐에 따라 탐색 및 분할에 소요되는 시간이 결정되기 때문에 피봇의 선택이 매우 중요한 정렬 알고리즘이다.

최선의 경우 : O(nlogn)	최악의 경우 : O(n^2)

^{퀵 정렬 시간 복잡도 (출처 : https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html)}

그럼에도 불구하고, 퀵 정렬은 평균 시간 복잡도가 매우 우수하기 때문에 가장 자주 사용된다.

따라서 피봇 값을 선택할 때 시간 복잡도를 낮출 수 있는 방식을 사용하는 것이 좋다. 예컨대, 1) 정해진 위치가 아니라 랜덤하게 피봇값을 선택하거나, 2) 몇 개의 값을 샘플링해 중앙값에 가까운 피봇을 선택하거나, 3) 배열의 첫 값과 중앙값, 그리고 마지막 값 중 크기가 중간인 값을 사용할 수 있다.

코드 구현

배열의 중앙에 있는 값을 피봇으로 선택해 구현한다.

• in-place 방식 : 정렬과 파티션, 2개의 내부 함수로 나눈다.
  • 정렬 함수는 재귀 함수로, 정렬 범위의 시작 인덱스와 끝 인덱스를 인자로 받는다.
  • 파티션 함수는 정렬할 범위를 인자로 받아 피봇의 값을 구한다. 이 함수 내에서는 피봇의 좌우측 값들을 정렬하고, 분할 기준점의 인덱스를 피봇으로서 반환한다.
    • 왼쪽 인덱스(L)를 계속해서 증가시키고, 오른쪽 인덱스(R)를 계속해서 감소시키기 위한 while문을 작성한다. while문은 두 인덱스가 서로 만날 때까지 반복된다.
      • 왼쪽(L)에서 오른쪽(R)으로 이동하며 피봇과 비교해 피봇보다 큰 값의 인덱스를 찾는다.(피봇보다 큰데 좌측에 있는 값을 찾는다.)
      • 오른쪽(R)에서 왼쪽(L)으로 이동하며 피봇과 비교해 피봇보다 작거나 같은 값을 찾는다.(피봇보다 작은데 우측에 있는 값을 찾는다.)
      • 두 인덱스가 서로 만나지 않는다면, 왼쪽(L) 인덱스의 값과 오른쪽 인덱스(R)의 값의 위치를 바꾼다.
    • 두 인덱스가 만나 while문을 빠져나오면, 다음 재귀 호출의 기준점이 될 시작 인덱스(L)를 반환한다.

def QuickSort(a, begin, end):
    if begin < end :
        p = Partition(a, begin, end) # 분할 기준 인덱스
        QuickSort(a, begin, p-1) # 왼쪽 배열에 대해 재귀 호출
        QuickSort(a, p+1, end) # 오른쪽 배열에 대해 재귀 호출
    return a
        
def Partition(a, begin, end):
    pivot_idx = (begin + end) // 2 # 피봇 인덱스 : 중간 위치로 설정.
    print(a[pivot_idx]) # 피봇 값 확인 위해
    L = begin
    R = end
    while L < R: # L이랑 R 만날 때까지 아래 과정 반복
        while (a[L] < a[pivot_idx] and L < R) : # 피봇 값보다 왼쪽에 있는데 작다면 L 증가 = 피봇값보다 크거나 같은데 왼쪽에 있는 원소 찾기.
            L += 1
        while (a[R] >= a[pivot_idx] and L < R) : # 피봇 값보다 오른 쪽에 있는데 크다면 R 증가 = 피봇값보다 작은데 오른쪽에 있는 원소 찾기.
            R -= 1
        if L < R : # 위의 과정을 거쳤는데 만나지 않은 경우
            if L == pivot_idx : # L이 피봇 값이면
                pivot_idx = R # 피봇을 오른쪽으로 바꾸기
            a[L], a[R] = a[R], a[L] # 만나지 않았다면, L과 R 위치의 원소 바꾸기
    a[pivot_idx], a[R] = a[R], a[pivot_idx]
    return R

• 조금 더 간결하고 이해하기 쉬운 구현을 적용하면 다음과 같다. 그러나, 이 방식은 매 번 재귀 호출을 진행할 때마다 새로운 리스트를 생성하기 때문에, 메모리 사용 측면에서 매우 비효율적이다. 따라서 원리만 이해하고 넘어가도록 한다.
  • 피봇보다 작은 값, 동일한 값, 큰 값을 저장할 3개의 리스트를 생성한다.
  • 반복문을 통해 각 값과 피봇 값을 비교한 후, 해당하는 리스트에 추가한다.
  • 작은 값과 큰 값을 담고 있는 왼쪽과 오른쪽의 배열을 대상으로, 퀵 정렬 함수를 재귀적으로 호출한다.
  • 재귀 호출의 결과를 크기 순으로 합쳐 정렬된 리스트를 얻는다.

def QuickSort(a):
    if len(a) <= 1:
        return a
    # 피봇 선택
    pivot = arr[len(arr)//2]
    lesser_a, equal_a, greater_a = [], [], []
    for num in a:
        if num < pivot:
            lesser_a.append(num)
        elif num > pivot:
            greater_a.append(num)
        else:
            equal_a.append(num)
    return QuickSort(lesser_a) + equal_a + QuickSort(greater_a)