[Algorithm] 선택정렬

선택 정렬

선택 정렬은 주어진 자료 중 가장 작은(혹은 가장 큰) 값의 원소부터 차례대로 선택하여 위치를 교환해 나간다. 학교 다닐 때 키순서대로 줄을 섰던 것을 떠올리면 된다. 가장 작은(혹은 가장 큰) 수부터 정렬하기 시작하여 위치를 교환하는 정렬 알고리즘이다.

이를 적용하기 위해 먼저 셀렉션 알고리즘에 대해 알아보자.

셀렉션 알고리즘

셀렉션 알고리즘은 자료에서 k번째로 큰(혹은 작은) 원소를 찾는 알고리즘으로, 최솟값, 최댓값 혹은 중간값을 찾을 때 주로 적용한다.

• 1번째부터 k번째 순번까지 작은 원소들을 찾아 list의 앞쪽으로 이동시킨다.
• list의 k번째 원소를 반환한다.

def SelectAlgorithm(list, k):
    for i in range(k): # k번째 순번까지
        min_idx = i
        for j in range(i+1, len(list)): # 뒤의 원소가 앞의 원소보다 크다면 
            if list[min_idx] > list[j]: # 최소 idx 교체.
                min_idx = j 
        list[i], list[min_idx] = list[min_idx], list[i] # i번째와 자리 바꿈.
    return list[k-1] # k번째로 작은 수 반환

선택 정렬에의 적용

위와 같은 셀렉션 알고리즘을 전체 자료에 k = 1로 생각하고 적용하면, 그것이 바로 선택 정렬이다.

^{이미지 출처 : https://www.fun-coding.org/Chapter12-selectionsorting.html}

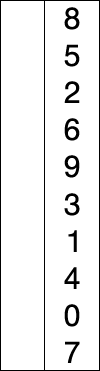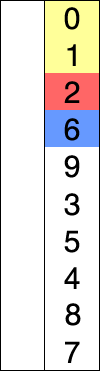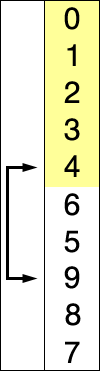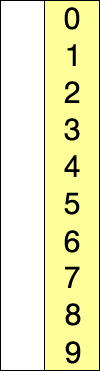
정렬을 수행하는 방법은 다음과 같다.

1. 주어진 리스트에서 최솟값(혹은 최댓값)을 찾는다.
2. 그 값을 리스트의 맨 앞 값과 교환한다. 리스트에서 맨 앞 원소는 정렬이 완료된다.
3. 맨 처음 위치를 제외한 나머지 리스트를 대상으로 위의 과정을 반복한다.

예) 64 25 10 22 11을 오름차순으로 선택정렬하는 과정

정렬 원소 미정렬원소

리스트	최솟값	맨 앞	정렬 결과
64 25 10 22 11	10	64	10 25 64 22 11
10 25 64 22 11	11	25	10 11 64 22 25
10 11 64 22 25	22	64	10 11 22 64 25
10 11 22 64 25	25	64	10 11 22 25 64

시간 복잡도

총 O(N^2)의 시간 복잡도를 가진다.

앞에서부터 한 칸씩 진행하고, 한 칸씩 진행할 때마다 전체 칸을 돌아야 하기 때문이다. 즉, 반복문을 통해 모든 인덱스의 값에 접근해야 하기 때문에 기본적으로 O(N)의 시간복잡도를 갖는다. 또한 하나의 루프 안에서 현재 인덱스의 값과 다른 인덱스의 값을 비교하여 최솟값을 찾아야 하므로, 인덱스 위치에 따라 또 O(N)의 시간을 필요로 한다.

코드 구현

• 뒷 순번의 인덱스로 갈수록 비교할 범위가 줄어든다.
• 안쪽 반복문에서는 현재 인덱스부터 마지막 인덱스까지 최솟값의 인덱스를 찾아내고, 바깥쪽 반복문에서 최솟값의 인덱스와 현재 인덱스에 있는 값을 교환한다.

def SelectionSort(a):
    for i in range(len(a)-1):
        min_idx = i
        # 최솟값 인덱스 찾기
        for j in range(i+1, len(a)):
            if a[min_idx] > a[j]:
                min_idx = j
        # 최솟값 인덱스의 값과 위치 바꾸기
        a[i], a[min_idx] = a[min_idx], a[i]
    return a