SVD

6 분 소요

선형대수학의 특잇값 분해(Singular Value Decomposition, 이하 SVD)는 추천 시스템의 matrix factorization 혹은 자연어처리의 latent semantic analysis 등 머신러닝, 딥러닝에서 자주 활용되는 개념이다.

참고: 선행 개념

기초가 없어서 그런가, 선행되는 개념들을 공부하고 넘어 오는 데에만 며칠이 소요되었다. 본 포스트에서는 다루지 않겠지만, SVD를 이해하기 위해서는 다음의 개념이 ~~대충이라도~~ 잡혀 있어야 한다.

선형변환

직교(벡터의 직교 및 정규직교, 직교행렬)

고윳값 분해

아래 나올 개념들은 시간 관계 상 깊이 공부하지는 못했지만, 나중에 공부해서 정리하면 좋을 개념들이다.

기저

rank

주성분 분석

1. 정의

SVD란, 임의의 $m \times n$ 직사각 행렬을 다음의 세 가지 행렬로 대각화하여 분해하는 방법을 말한다.

\[A = U \Sigma V^{T}\] \[U = m \times m \ 직교행렬 \\ \Sigma = m \times n \ 대각행렬 \\ V = n \times n \ 직교행렬\]

참고 : SVD의 position

행렬의 분해라는 개념이 와닿지 않아 위키피디아를 참고했다.

결과적으로는 특정 목적이 있어서 행렬을 분해해서 이해하고 싶은 것이고, 그 분해 방법이 여러 가지가 있는데, 그 중에서도 고윳값에 근거하여 분해하는 방법 중 하나가 SVD라는 것이다. 따라서 나는 데이터 분석 및 머신러닝, 딥러닝에서 왜 행렬을 분해하는지, 그 활용이 어떤지에 초점을 두어 SVD를 이해하고자 한다.

위의 개념을 시각화하면 다음과 같다.

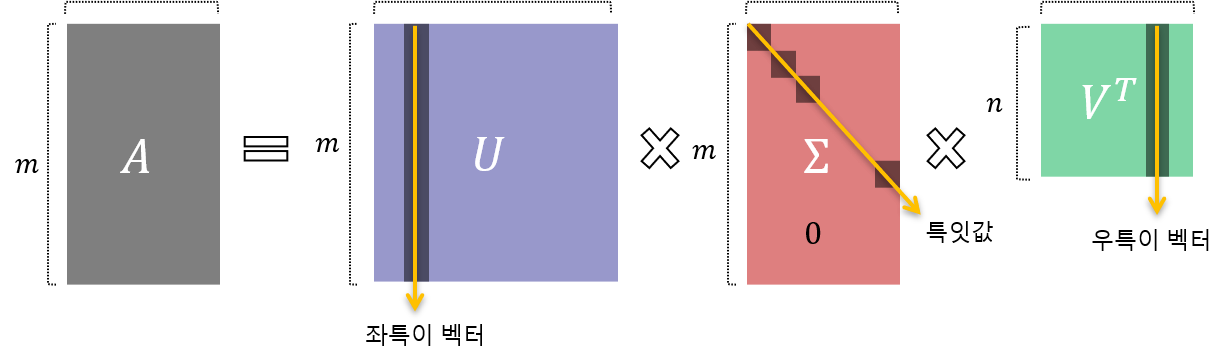
svd-concept

고윳값 분해가 정방행렬에만 적용할 수 있는 것과 달리, SVD는 모든 행렬에 대해 다 적용할 수 있다. 분해 후 결과에서 유의해야 하는 것은, 행렬 $A$가 애초에 직사각 행렬이었으므로, $m<n$인지 $m>n$인지에 따라 중간의 대각 행렬의 모양이 달라진다는 것이다.

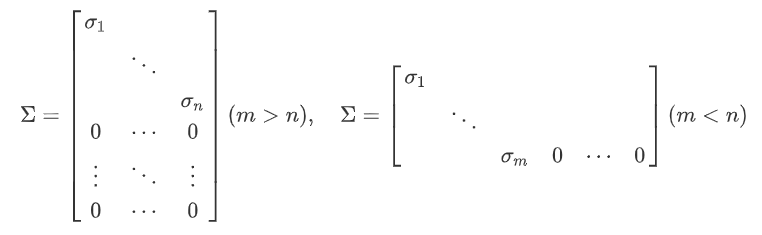
svd-sigma

특이 벡터

SVD 결과로 나오는 각 행렬의 왼쪽 행렬을 이루는 열 벡터들을 좌특이 벡터 (left-singular vector), 오른쪽 행렬을 이루는 열 벡터들을 우특이 벡터 (right-singular vector)라고 한다.

좌특이 벡터로 이루어진 행렬 $U$와 우특이 벡터로 이루어진 행렬 $V$를 구하기 위해서는 각각 $AA^T$, $A^TA$를 고윳값분해하여 얻은 고유 벡터들의 행렬을 구하면 된다.

특잇값

특잇값(singular value)이란, $m \times n$ 행렬 $A$에 대해 $\lambda_1, \lambda_2, … \ \lambda_n$이 $A^TA$의 고윳값일 때,

\[\sigma_1 = \sqrt{\lambda_1}, \sigma_2 = \sqrt{\lambda_2}, ... \ , \sigma_n = \sqrt{\lambda_n}\]

을 $A$의 특잇값이라 한다.

즉, 직사각행렬 $A$와 $A^T$를 곱하면 정방행렬이 되고, 그 정방행렬을 고윳값분해하면 나오는 값들에 square root를 취하면 그게 특잇값이란 의미이다. 이 과정에서 다음의 사실들이 성립한다는 것이 증명되어 있으나, 그것은 본 포스트의 범위를 넘는 내용이므로 정리하지 않는다.

$A \cdot A^T = A^T \cdot A$ 이므로, $A \cdot A^T$와 $A^T \cdot A$는 동일한 고윳값을 갖는다.
$A \cdot A^T$와 $A^T \cdot A$의 고윳값은 모두 0 이상이다. 즉, $A \cdot A^T$와 $A^T \cdot A$는 모두 positive semi-definite 행렬이다.

이렇게 구한 특잇값들 중 $min(m, \ n)$의 개수만큼을 대각 원소에 나타낸 것이 SVD 결과로 나오는 중간의 대각행렬이 된다. 이 때, 대각 원소가 큰 순서대로 나타내는 것이 수학적 관행이다.

2. 기하학적 의미

선형대수학에서 행렬 $m \times n$ 행렬 $A$는 (기하학적으로) $n$차원 공간에서 $m$차원 공간으로의 선형변환을 나타낸다. 이 때, SVD는 $n$차원 공간에서 $m$차원 공간으로의 선형변환을 의미하는 행렬 $A$를 다음과 같은 두 개의 회전변환과 각 좌표 성분의 스케일 변환으로 분해하여 이해하는 것을 의미한다.

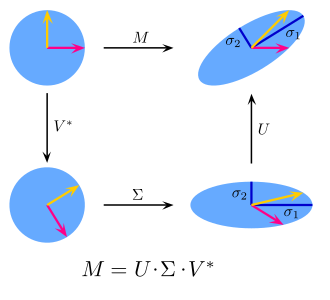
svd-geometrically

^{출처: 위키피디아 SVD, *는 transpose}

이 때 SVD가 나타내는 행렬 $A$의 선형변환 순서는 다음과 같다.

$V^T$에 해당하는 선형변환: 기존 벡터의 크기는 유지하면서(직교 행렬), 방향만 변화 → 형태 그대로
$\Sigma$에 해당하는 선형변환: 방향이 변화된 벡터의 각 좌표 성분을 특잇값의 크기만큼 스케일 변화 →형태 변화
$U$에 해당하는 선형변환: 방향 변화, 스케일 변화된 벡터를 다시 크기는 유지하면서 방향만 변화 → 형태 그대로

결국 해당 선형변환에서 원래 벡터가 나타내는 도형의 형태를 변화시키는 것은 $\Sigma$이다. $m$과 $n$의 크기가 어떠한지에 따라, 이 스케일 변화는 원래 벡터의 차원에서 0을 덧붙여 차원을 확장한 후에 방향을 변화시킬지, 혹은 낮은 차원으로 ~~일종의~~ 투영을 시킨 뒤 방향을 변화시킬지를 결정한다.

3. 활용

SVD가 선형대수학에서 활용되는 분야는 다음과 같다.

선형시스템의 풀이: 선형연립방정식으로 이루어진 문제의 풀이
행렬 근사 및 데이터 압축: 특잇값의 개수를 제한함으로써 원래 행렬에 비슷한 행렬을 얻어내어 근사하거나, 데이터를 압축

이 중, 전자는 $Ax = b$의 선형시스템을 풀이하는 과정에서 pseudo-inverse 행렬을 구하기 위해 활용되는 것인데, 이보다는 후자의 개념이 내가 더 공부하고 싶은 분야와 연관이 있으므로 이를 더 깊이 알아보도록 한다.

reduced SVD

1의 개념에서 설명한 것과 같이 행렬을 분해하는 것은 full SVD라고 불린다. 이렇게 행렬을 분해할 경우, 이론 상 분해 결과로 나타나는 세 행렬을 곱하면 원래의 행렬이 복원되어야 한다. (이론 상이라고 한 것은, 실제로 코드로 SVD를 구현해 보니 수의 크기에 따라서 완벽하게 복원되지 않는 경우가 존재했기 때문이다.)

이와 달리, full SVD에서 특잇값의 개수를 제한하고, 그에 해당하는 특이벡터들을 없애주는 것을 reduced SVD라고 한다. 원래 full SVD를 수행했을 때 행렬을 다음과 같이 나타낼 수 있다.

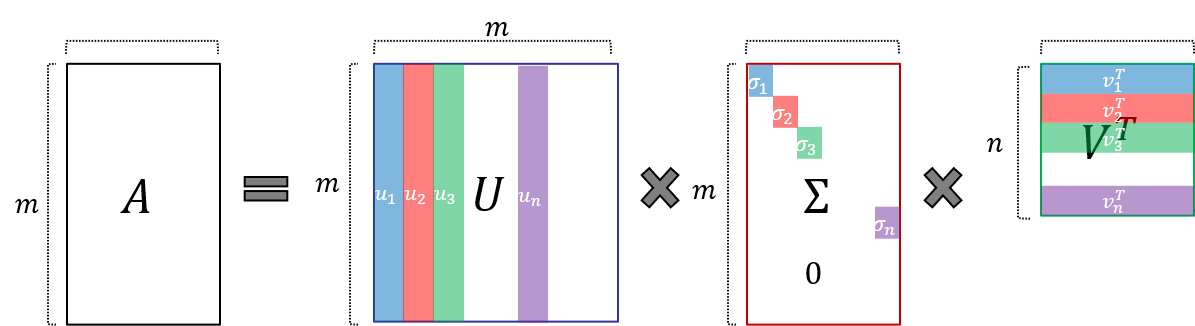
svd-low-rank

\[A = \sigma_1 \cdot u_1 \cdot v_1^T + \sigma_2 \cdot u_2 \cdot v_2^T + \cdots + \sigma_r \cdot u_r \cdot v_r^T\]

참고 : SVD와 low-rank approximation

SVD 결과로 나타나는 특잇값 중 0이 아닌 원소의 개수가 행렬의 rank를 나타낸다고 한다. 일단 여기서는 rank까지는 다루지 말고, 그냥 속 편하게 $r = n$이라고 생각하자. 특잇값의 개수에 제한을 두어 SVD를 수행하는 것 자체가 행렬을 저차원으로 압축하는 것과 연관이 있는 듯하고, 이 과정에서 rank와 기저 개념을 더 학습해야 할 필요를 느꼈다.

svd-low-rank-recs

위의 식에서 우변을 이루는 각각의 항이 모두 행렬 $A$와 같은 $m \times n$ 크기의 행렬이므로 각각을 모두 더하면 원래 행렬이 된다. 여기서 각각의 행렬의 랭크는 1이 된다(특잇값과 두 개의 열벡터의 곱이므로).

그러면 여기서 특잇값의 개수를 1로 제한하면 원래 행렬 $A$를 모든 정보를 사용하여 나타내지 않고, $\sigma_1 \cdot u_1 \cdot v_1^T$ 만을 사용하여 나타낸다는 의미가 된다. 즉, 원래 행렬을 랭크가 1인 행렬로 근사하는 것이다. 그 개수가 2가 되면 원래 행렬 $A$를 $\sigma_1 \cdot u_1 \cdot v_1^T$과 $\sigma_2 \cdot u_2 \cdot v_2^T$ 두 행렬을 이용하여 나타낸다는 의미이다. 결과적으로 특잇값의 개수를 제한한다는 것은 원 행렬의 모든 정보를 활용하지 않고 일부 정보만을 활용하여 원 행렬에 근사한 행렬을 구하는 것이기도 하다. 당연히 특잇값이 큰 수부터 작은 수까지 정렬되어 있으므로, 가장 큰 특잇값을 갖는 행렬부터 선택해야 정보를 더 많이 보존하면서 근사할 수 있다.

서두가 길었지만, 결론적으로 말하면 full SVD의 결과에서 특잇값의 개수를 제한하는 reduced SVD를 수행하게 되면, 분해 결과로 나타나는 세 행렬의 곱이 원래 행렬이 아니라, 원래 행렬의 근사 행렬이 된다. ~~분해 결과에서 일부 원소가 소실되었으니 당연한 결과이다.~~ 이러한 reduced SVD는 다음과 같은 세 가지 종류로 나누어 진다.

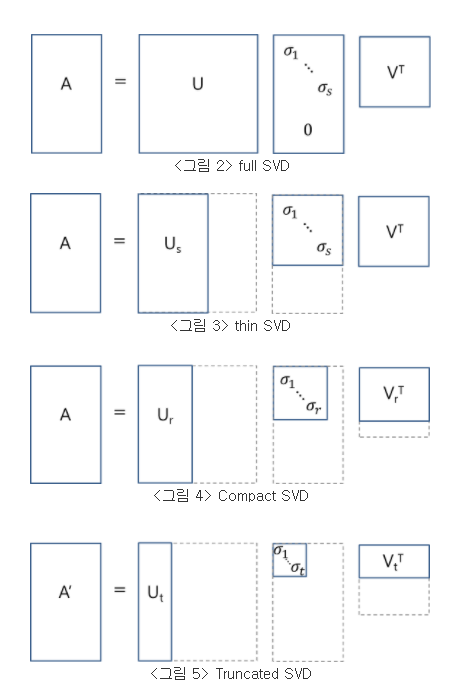
reduced-svd

^{이미지 출처: https://darkpgmr.tistory.com/106}

thin SVD: $\Sigma$에서 대각원소가 아닌 원소들을 제거하고, 그에 대응하는 특이벡터들을 제거
compact SVD: $\Sigma$에서 비대각원소 부분과 대각원소 중 0인 부분을 제거하고, 그에 대응하는 특이벡터들을 제거
truncated SVD: $\Sigma$에서 비대각원소 부분과 대각원소 중 0인 부분에 더해 대각 원소 중 0이 아닌 부분까지 제거하고, 그에 대응하는 특이벡터들을 제거. 그냥 쉽게, $\Sigma$에서 몇 개까지 남길 것인지를 결정해서 남길 대각원소들을 제외하고 그 외의 모든 원소 및 그에 대응하는 특이벡터들을 제거한다고 보면 된다.

reduced SVD를 한다고 하면, 보통 데이터 압축 및 행렬 근사를 목적으로 하기 때문에, 주로 가장 좁은 개념인 truncated SVD를 지칭하는 듯하다.

truncated SVD에서 몇 개까지의 특잇값을 남길 것인지(이하 $t$)가 하이퍼파라미터가 되고, $t$에 따라 SVD 후 원래 행렬로 얼마나 복원될지가 결정된다. 당연히 $t$가 클수록 데이터 압축률이 작지만 원 행렬에 더 잘 근사되고, 작아질수록 데이터 압축률은 커지지만 원 행렬과 근사한 정도가 작아진다. 그리고 이를 이용해 원 행렬에 근사한 행렬을 구함으로써, 해당 행렬이 나타내는 데이터의 차원을 축소할 수도 있다.

머신러닝, 딥러닝에서의 활용

SVD를 어떤 분야에서 활용하는지를 이해하기 앞서, SVD를 선형대수학 기법을 이용하여 수행한 후 다른 태스크에 활용할지, 혹은 신경망을 이용해(예컨대, 임베딩 레이어 이용) 행렬을 분해할지를 결정해야 한다. 후자는 SVD 자체를 활용한다기 보다는 SVD의 개념을 응용하여 신경망 모델을 짜야 한다고 보아야 할 듯하다. 즉, 신경망이 latent factor를 알아내도록 행렬을 분해할 때, 입력 데이터를 latent factor 공간으로 매핑하는 단계에서 SVD 개념을 활용하도록 하는 것이다.

어쨌든 머신러닝, 딥러닝에서 SVD를 사용한다고 하면, 주로 다음의 영역에서 사용된다고 보아도 무방하다.

첫째, latent factor를 찾는 모델이다. SVD 결과로 나타나는 특잇값의 대각행렬 $\Sigma$를 latent factor로 해석하고, 각 데이터와 latent factor 간 관계를 찾아내기 위한 모델로 해석하는 것이다. 각 영역별로 풀고자 하는 문제가 있을 것이고, 그 문제에서 활용할 요인-잠재요인-요인 간 관계를 찾고자 할 때 SVD를 활용해 행렬을 분해하는 것이다. 요즘 업무 과정에서 공부하고 있는 추천 시스템을 예로 들면, user-item matrix를 user-latent factor-item matrix로 분해하는 데에 활용한다. 이렇게 활용할 때에는 latent factor를 어떻게 해석할지의 문제가 남게 된다.

둘째, 데이터의 압축 및 차원 축소이다. 원 데이터의 크기가 너무 클 때 truncated SVD를 통해 원 데이터 행렬을 압축할 수 있다. 차원 축소이기도 하다. 참고로, SVD 결과는 수학적으로 PCA와 동일하다.

4. 구현

NumPy, Scipy 등의 패키지를 쓰면 쉽게 SVD를 구현할 수 있다. 이미지 데이터를 가지고, 어떻게 데이터를 압축할 수 있는지 실험해 보았다.

# module import
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

# load image
ruby = Image.open('./ruby.jpg')

# transform original image: gray scale
ruby_gray = ruby.convert('I')
plt.imshow(ruby_gray)
ruby_arr = np.array(ruby_gray) # shape: (3024, 4032)

# SVD
u, sigma, vt = np.linalg.svd(ruby_arr)

# reconstruct image
for i in range(1, 6):
    reconstructed_ruby = u[:, :i] @ np.diag(sigma[:i]) @ vt[:i, :]
    plt.imshow(reconstructed_ruby, cmap='gray')
    plt.title(f"reconstructed image when t={i}")
    plt.show()