[LEETCODE] 빗물 트래핑

문제

출처: https://leetcode.com/problems/trapping-rain-water/description/

풀이

구현 1. 가장 높은 벽의 높이 기준

빗물을 받기 위해 직전까지 가장 높았던 벽보다 벽의 높이가 낮아야 한다. 벽의 높이를 나타내는 height 배열을 순회하며, 해당 순번 직전까지 가장 높았던 벽의 높이를 저장하는 변수(max_idx)를 둔다.

해당 변수는 가장 높은 벽을 지나기 전과 후에 따라 갱신 로직이 달라진다.

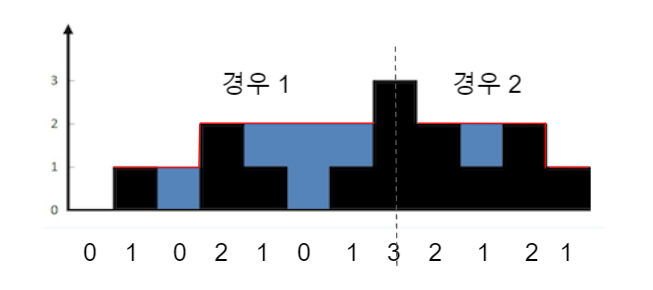
• 가장 높은 벽의 높이: max_height
• 가장 높은 벽을 지나기 전: 현재 벽의 높이가 max_height 변수의 값보다 높은 경우 max_idx 값 갱신
• 가장 높은 벽을 지난 후: 현재 벽의 높이가 max_height 변수의 보다 낮은 경우 max_idx 값 갱신
• 가장 높은 벽을 지난 후, 현재 지나고 있는 벽의 높이가 max_idx에 저장된 값보다 커지는 경우는 있을 수 없음

# 42ms, 14.7MB 
class Solution: 
    
    def split(self, height: List[int]) -> Tuple[List[int], List[int]]:
    '''최고 높이 벽을 지나기 전과 후로 분리'''
    max_height = max(height) 
    max_idx = height.index(max_height) # 최고 높이 벽의 위치 
    return height[:max_idx+1], height[max_idx:][::-1] 
    
    def collect(self, height: List[int]) -> int: 
    '''리스트 내 쌓이는 빗물 양 계산''' 
    	wall = 0 # 이전까지 가장 높은 벽의 높이 
    	water = 0 # 쌓인 물의 양 
    	for h in height: 
    		if h > wall: 
        		wall = h 
            	water += wall - h 
    	return water 
    
    def trap(self, height: List[int]) -> int: 
    '''왼쪽 리스트와 오른쪽 리스트에서 쌓이는 빗물 최종 양 계산''' 
    
    # 빈 리스트가 입력으로 들어오는 예외 처리 
    if not height: 
    	return 0 
    
    l_height, r_height = self.split(height)
    return self.collect(l_height) + self.collect(r_height)

구현 2. 투포인터 이용

height 배열을 순회하는 2개의 포인터를 두어 순회한다.

• 최대 높이 기준 좌측, 우측 포인터를 둠
• 우측 포인터가 더 크다면 좌측 포인터를 우측으로 한 칸, 좌측 포인터가 더 크다면 우측 포인터를 한 칸 이동
• 최대 지점에서 두 포인터가 만나면 순회 중단

def trap(self, height: List[int]) -> int: 
	if not height: 
    	return 0 
    
    volume = 0 
    left, right = 0, len(height) - 1 # 포인터 
    left_max, right_max = height[left], right[max] # 포인터 높이 초깃값 
    
    while left < right: 
    	left_max, right_max = max(height[left], left_max), max(height[right], right_max) 
    
    # 우측으로 이동 
    if left_max <= right_max: 
    	volume += left_max - height[left] 
      left += 1 
    # 좌측으로 이동 
    else: 
    	volume += right_max - height[right] 
      right -= 1 
    
    return volume

구현 3. 스택 이용

배열을 순회하며 스택을 쌓아 나간다. 현재 물 높이가 스택에 담겨 있는 이전 물 높이보다 높다면, 그 격차만큼 물 높이를 채운다.

• 현재 높이가 이전 높이보다 작다면 스택에 현재 인덱스를 넣음
• 현재 높이가 이전 높이보다 크거나 같다면 스택에서 높이가 더 작은 인덱스를 꺼냄

def trap(self, height: List[int]) -> int: 
    stack = [] 
    volume = 0 
    
    for i in range(len(height)): 
      
      # 현재 높이가 스택에 있는 인덱스의 높이보다 크다면 계속 꺼내기
      while stack and height[i] > height[stack[-1]]: 
          top = stack.pop() 

          if not len(stack): 
            break 
            
          # 물 높이 더해 주기 
          distance = i - stack[-1] -1 
          waters = min(height[i], height[stack[-1]]) - height[top] 
          volume += distance * waters 
			
      # 현재 높이가 스택에 있는 인덱스보다 작다면 스택에 추가
      stack.append(i) 
        
    return volume

다른 사람의 풀이

출처: https://leetcode.com/problems/trapping-rain-water/solutions/1311501/A-Python-DP-based-solution/

DP를 사용한 풀이이다. 어느 지점에서든 해당 지점의 왼쪽에서의 최대 높이와 오른쪽에서의 최대 높이 중 더 작은 값에서 해당 지점의 높이를 빼면 빗물의 양을 구할 수 있다.

class Solution:
    def trap(self, height: List[int]) -> int:
        if len(height) < 3:
            return 0
        trap = 0
        max_left, max_right = [0] * len(height), [0] * len(height)
        max_left[0], max_right[-1] = height[0], height[-1]
        for i, h in enumerate(height):
            if i > 0:
                max_left[i] = max(max_left[i-1], height[i])
        for i, h in reversed(list(enumerate(height))):
            if i < len(height) - 1:
                max_right[i] = max(max_right[i+1], height[i])
        for i, h in enumerate(height):
            trap += max(0, min(max_left[i], max_right[i]) - h)
        return trap

기타

• O(n^2) 풀이를 O(n)으로 해결하는 것이 중요하다. 만약 height 배열 순회하며, 뒤의 원소들의 높이까지 살폈다면, O(n^2) 풀이가 된다.
• 구현2에서 해당 위치에서의 값을 기억해야 하기 때문에, 스택에 인덱스를 사용한다. 알고리즘 문제 풀이에 종종 사용되므로, 기억해 두자.
• 투 포인터 사용에 익숙해질 필요가 있다.